设有一棵二叉树，如图：

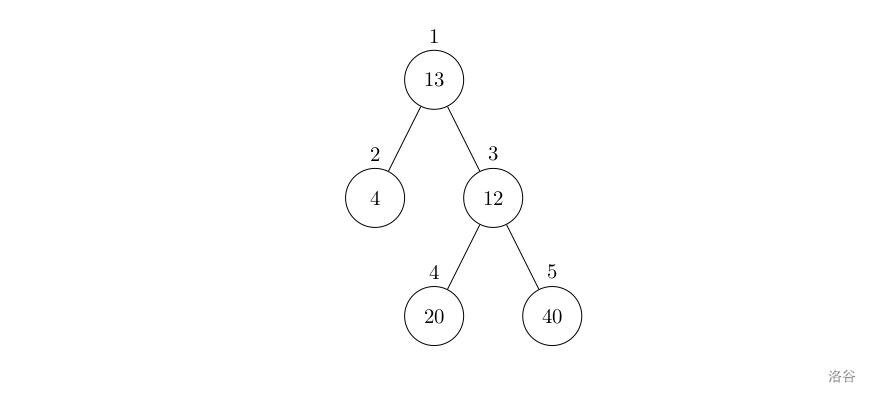
其中，圈中的数字表示结点中居民的人口。圈边上数字表示结点编号，现在要求在某个结点上建立一个医院，使所有居民所走的路程之和为最小，同时约定，相邻接点之间的距离为 11。如上图中，若医院建在 11 处，则距离和 =4+12+2×20+2×40=136=4+12+2×20+2×40=136；若医院建在 33 处，则距离和 =4×2+13+20+40=81=4×2+13+20+40=81。

输入格式

第一行一个整数 n，表示树的结点数。

接下来的 n 行每行描述了一个结点的状况，包含三个整数 w,u,v，其中 w 为居民人口数，u 为左链接（为 00 表示无链接），v 为右链接（为 00 表示无链接）。

输出格式

一个整数，表示最小距离和。

输入输出样例

输入 #1复制

5						
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0

输出 #1复制

81

方法1（弗洛伊德）

#include<bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define PII pair<int,int >;
#define int long long 
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
 
using namespace std;
 
const int N = 210;
 int n;
int va[N];
int dis[N][N];
signed main()
{
    IOS;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
    	for(int j=1;j<=n;j++)
    	{
    		dis[i][j]=1e18;
    		if(i==j) dis[i][j]=0;
		}
	}
	for(int i=1;i<=n;i++)
	{
		int a,b;
		cin>>va[i]>>a>>b;
		if(a!=0) dis[i][a]=dis[a][i]=1;
		if(b!=0) dis[i][b]=dis[b][i]=1;
	}
		for(int k=1;k<=n;k++)
	{
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=n;j++)
			dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
		}
	}
	int minn=1e18;
	for(int k=1;k<=n;k++)
	{
		int sum=0;
		for(int i=1;i<=n;i++) sum+=dis[i][k]*va[i];
		minn=min(minn,sum);
	}
	cout<<minn;
	return 0;
}

方法2（搜索dfs)

#include<bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define PII pair<int,int >;
#define int long long 
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
 
using namespace std;
 
const int N = 1e6+10;
 
int n;
long long minn=1e18;
int sum=0;
int va[N];
int vis[N];
vector<int>e[N];
void dfs(int now,int dep)
{
	vis[now]=1;
	sum+=va[now]*(dep-1);
	for(auto spot:e[now])
	{
		if(vis[spot]==0) dfs(spot,dep+1);
	}
}
signed main()
{
    IOS;
    cin>>n;
	for(int i=1;i<=n;i++)
	{
		int a,b;
		cin>>va[i]>>a>>b;
		if(a!=0) e[i].pb(a),e[a].pb(i);
		if(b!=0) e[i].pb(b),e[b].pb(i);
	}
	for(int i=1;i<=n;i++)
	{
		sum=0;
		for(int j=1;j<=n;j++) vis[j]=0;
		dfs(i,1);
		if(minn>sum) minn=sum;
	}
	cout<<minn;
}