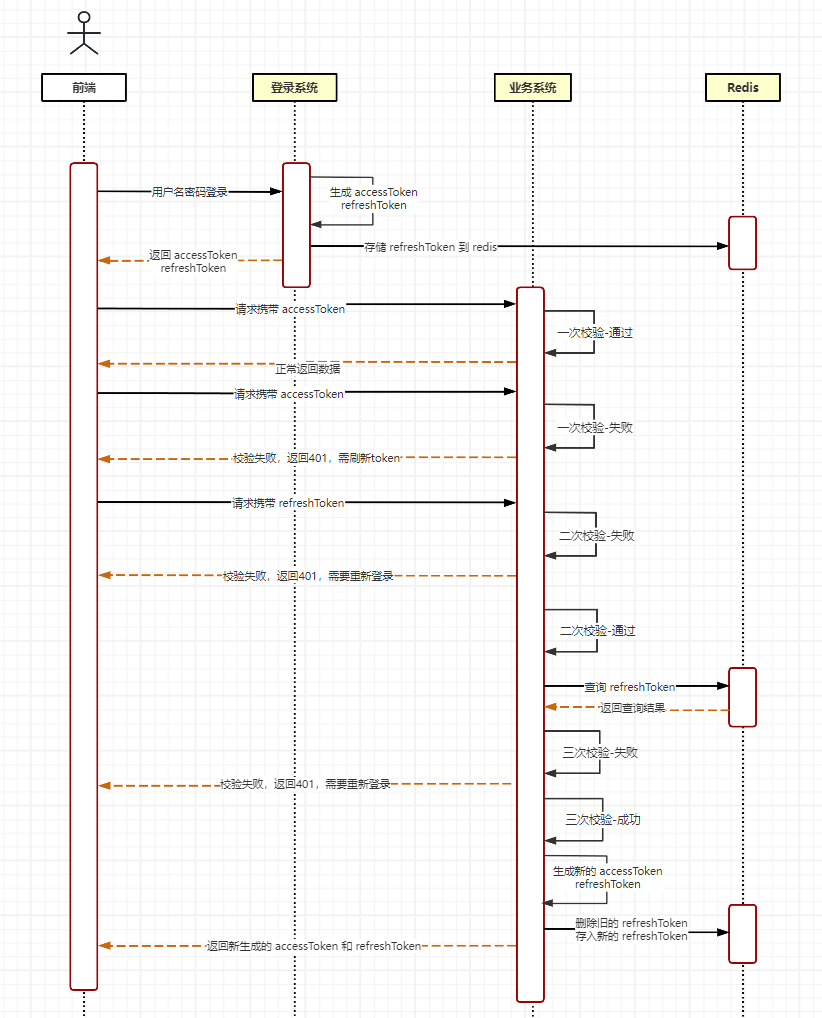
目录

Hypothesis Testing

Null Hypothesis

---

Hypothesis Testing

另一种引入不确定性的方法是陈述假设检验：两个组之间的均值差异是否在统计上与零（或其他任何值）不同？要回答这类问题，你需要回想正态分布的和或差也是正态分布。最终的均值将是两个分布的和或差，而方差则始终是两个方差的和：

如果你记不住，没关系。你可以随时使用代码和模拟数据来自己验证这一点：

  import seaborn as sns
 from matplotlib import pyplot as plt
 np.random.seed(123)
 n1 = np.random.normal(4, 3, 30000)
 n2 = np.random.normal(1, 4, 30000)
 n_diff = n2 - n1
 plt.figure(figsize=(10,4))
 sns.distplot(n1, hist=False, label="$N(4,3^2)$")
 sns.distplot(n2, hist=False, label="$N(1,4^2)$")
 sns.distplot(n_diff, hist=False,
 label=f"$N(-3, 5^2) = N(1,4^2) - (4,3^2)$")
 plt.legend();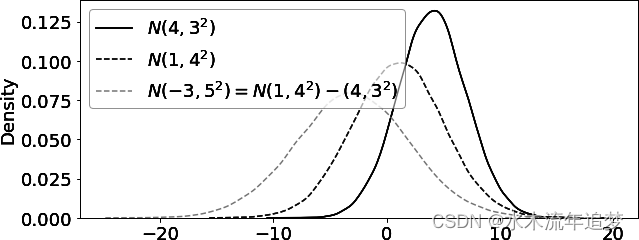

如果取两组数据，每组都有一个关联的分布，然后将一组从另一组中减去，最终会得到第三个分布。这个最终分布的均值将是两组均值之差，而标准差将是两个方差之和的平方根。既然我们讨论的是实验平均值的分布，可以将这些分布的标准差视为均值的标准误：

你可以利用这个概念来比较你的交叉销售邮件实验中的转化率。如果你取两个组的估计分布——比如说短邮件组和无邮件组——并从中减去一个，你就会得到差异的分布。有了这个分布，你可以轻松构造出两组均值之差的95%置信区间：

 diff_mu = short_email.mean() - no_email.mean()
 diff_se = np.sqrt(no_email.sem()**2 + short_email.sem()**2)
 ci = (diff_mu - 1.96*diff_se, diff_mu + 1.96*diff_se)
 print(f"95% CI for the difference (short email - no email):\n{ci}")
 
 95% CI for the difference (short email - no email):
 (0.01023980847439844, 0.15465380854687816)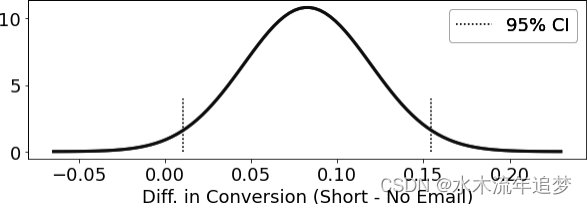

Null Hypothesis

通过这个置信区间，你可以回答关于所谓的零假设的问题。例如，你可以提出这样的假设：简短邮件与完全不发邮件相比，在转化率上没有差异。通常我们会用H0来表示零假设：

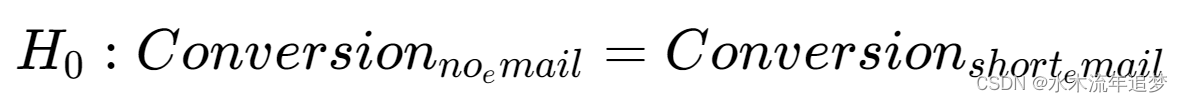
一旦你有了这个假设，接下来要问自己的问题是，“如果零假设是真的，我观察到如此大的差异的可能性有多大？”你会审视数据，看它是否符合你的零假设。如果不符合，你会说，如果零假设为真，看到这样的数据太奇怪了，因此你应该拒绝这个假设。 一种检验零假设的方式是使用你刚刚构建的置信区间。

注意，前面的95%置信区间并不包含零。同时，回想一下这是转化率差异的CI。因为零假设指出这个差异是零，但你看到置信区间完全在零之外，所以可以说如果零假设为真，看到这样结果的概率太低。因此，你可以以95%的置信度拒绝零假设。

当然，除了指出完全没有差异的零假设外，你还可以提出其他的零假设。例如，假设发送邮件存在一定的成本，这是非常现实的情况。即使没有显著的金钱成本，如果你向客户发送过多的邮件，最终他们可能会标记你为垃圾邮件发送者，这会关闭与他们的沟通渠道，导致未来销售额下降。在这种情况下，也许营销团队只有在转化率提升高于1%时才愿意推广交叉销售邮件。那么，你可以这样表述零假设：“转化率的差异是1%。”为了检验这个假设，你只需将置信区间移动，即从均值差异中减去1%即可：

 # shifting the CI
 diff_mu_shifted = short_email.mean() - no_email.mean() - 0.01
 diff_se = np.sqrt(no_email.sem()**2 + short_email.sem()**2)
 ci = (diff_mu_shifted - 1.96*diff_se, diff_mu_shifted + 1.96*diff_se)
 print(f"95% CI 1% difference between (short email - no email):\n{ci}")
 
 95% CI 1% difference between (short email - no email):
 (0.00023980847439844521, 0.14465380854687815)

由于这个95%CI也高于零，你也可以拒绝这个其他的零假设。然而，现在95%CI非常接近于零，这意味着你无法拒绝效果等于比如2%这样的数值的零假设，至少不能以95%的置信度来拒绝。