本教程介绍了直接线性变换 (DLT),这是一种用于解决以下类型方程组的通用方法:
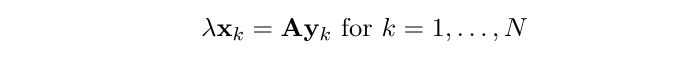
这种类型的方程经常出现在射影几何中。一个非常重要的例子是场景中的 3D 点与它们在相机图像平面上的投影之间的关系。这就是为什么我们要使用此设置来激发 DLT 的使用。
NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割
1、相机模型
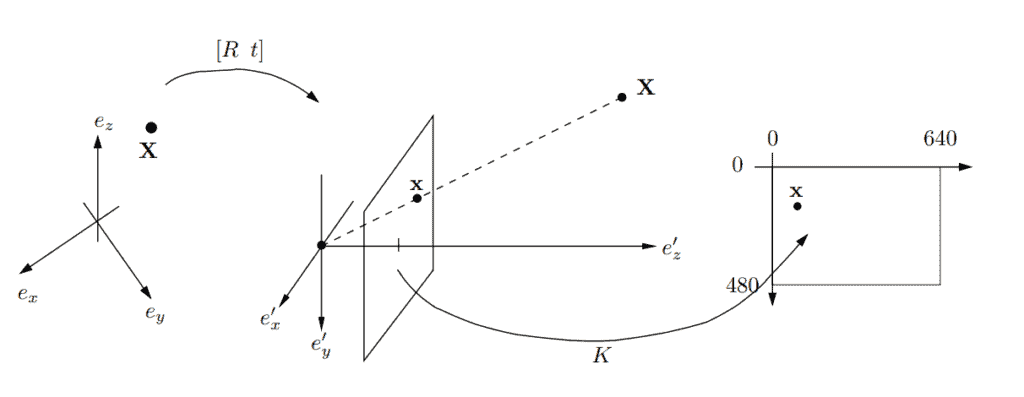
相机最常用的数学模型是所谓的针孔相机模型。由于相机的概念是在现实世界的物体和 2d 表示之间进行映射,因此相机模型由几个坐标系组成:
1.1 全局坐标
为了对相机位置和运动进行编码,我们使用参考坐标系 {e_x, e_y, e_z}(图的左侧部分)。在这个系统中,相机可以进行平移和旋转。平移表示为向量 t,旋转表示为 3x3 旋转矩阵 R。
通常,所有场景点坐标也在全球坐标系中指定,并且使用 R 和 t 将它们与相机坐标系关联起来,如下所示:
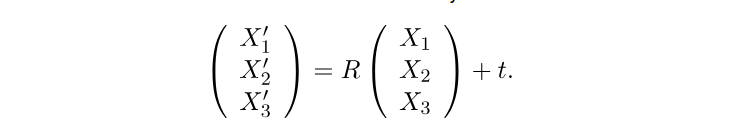
如果我们添加 1 作为额外维度,它就可以整齐地以矩阵形式表示。
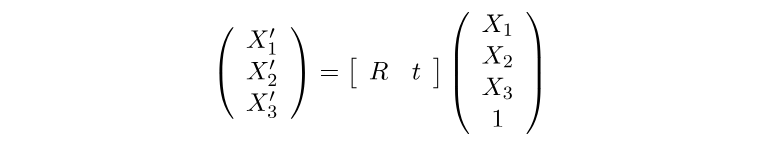
1.2 相机坐标
相机坐标系 {e'_x, e'_y, e'_z}(位于图的中间)有一个原点 C = (0,0,0),代表相机中心或针孔。为了生成场景点 X = (X_1, X_2,X_3) 的投影 x = (x_1, x_2, 1),我们在 X 和 C 之间形成一条线,并将其与平面 Z = 1 相交。
这个平面也称为图像平面,与它相交的线是视线。人们可能会注意到,与物理相机不同,投影平面位于针孔前面。这样做是为了方便,并且图像不会像在真实模型中那样上下颠倒。
1.3 内部参数
在针孔相机模型中,图像平面位于 R^3 中,这意味着投影以真实世界单位的长度给出。但是当我们谈论图像时,我们使用指定尺寸的像素。在我们的示例图中,我们使用 640 x 480 像素。为了转换它,我们使用从嵌入在 R^3 中的图像平面到真实图像的映射(图的右侧)。
此像素映射由可逆三角 3 x 3 矩阵 K 表示,其中包含相机的内部参数,即焦距、主点、纵横比和轴倾斜。
1.4 完整表示
最后,我们可以将相机模型的所有三个部分关联到一个方程中:
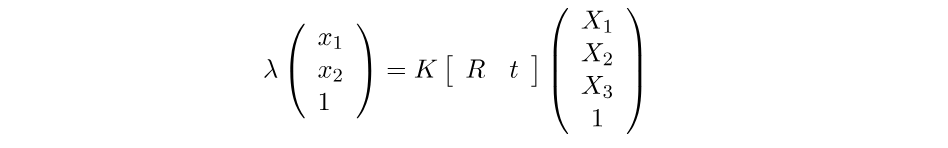
或者更简洁地说:
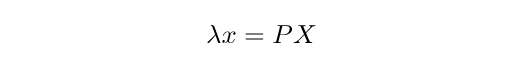
其中 P 称为相机矩阵。
上面的等式现在看起来就像 DLT 可以帮助我们找到矩阵 P 的确切类型(如果我们愿意的话)。
2、相机标定
但是为什么我们首先需要解决它呢?大多数时候,我们感兴趣的是找到相机矩阵 P 的 K 部分。因为如果知道 K,我们就能知道相机已校准。使用校准后的相机,我们可以进行镜头失真校正、从照片测量物体,甚至从相机运动中估计 3d 坐标等操作。
为此,我们首先需要至少 6 个手动测量的数据点,然后我们可以使用 DLT 方法计算相机矩阵 P,最后使用 RQ 分解将 P 分解为 K [R t]。
3、DLT标定方法
DLT 方法的第一步是制定一个齐次线性方程组,并通过找到近似零空间来求解它。为此,我们首先用行向量表示 P:
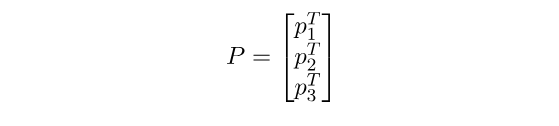
然后我们可以将相机方程写成:
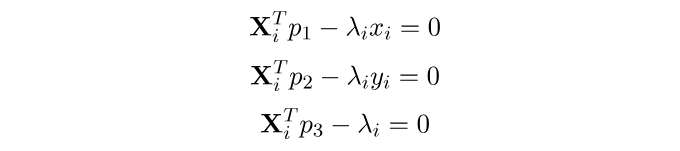
进而可以将其表示成矩阵形式:
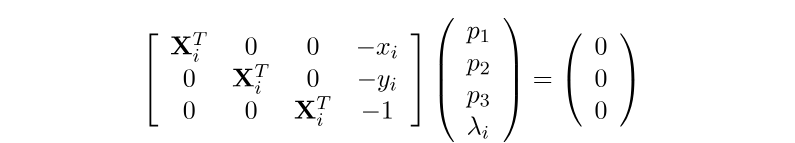
请注意,由于 X_i 是一个 4 x 1 向量,因此每个 0 实际上代表一个 1x 4 的零块,这意味着我们将一个 3 x 3 矩阵乘以一个 1 x 1 向量。
如果我们将所有测量数据点的所有投影方程堆叠在一个矩阵中,我们将得到一个形式如下的系统:
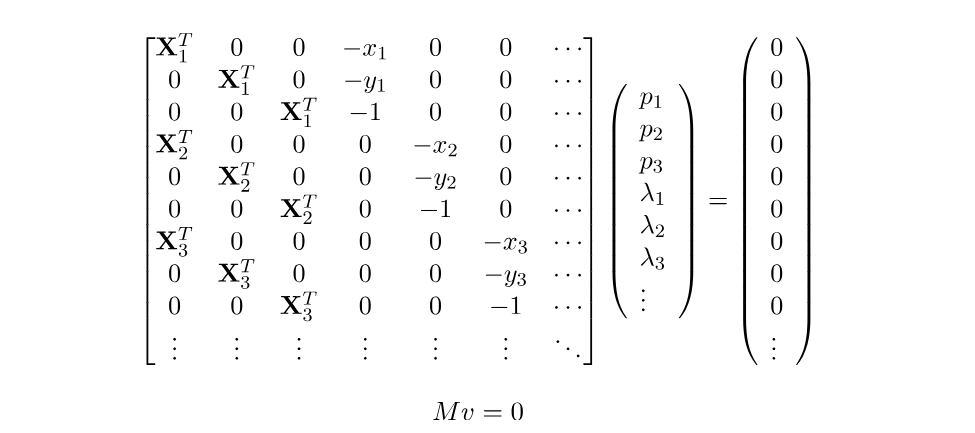
重新排列方程后,我们只需在 M 的零空间中找到一个非零向量即可求解系统。然而,在大多数情况下,由于测量时有噪声,不会有精确解。因此,寻找最小化总误差的解更为方便,本质上是求解最小二乘问题。
解决该问题的一种方法是使用奇异值分解 (SVD)。分解大矩阵 M 后,我们可以取与最小奇异值相对应的右奇异向量,这样我们就找到了相机矩阵 P。然后,我们可以使用前面提到的 QR 分解方法将 P 分解为 K [R t]}。
4、结束语
在本文中,我们研究了针孔相机模型,并通过尝试找到给定相机模型的固有参数来激发离散线性变换 (DLT) 的使用。以这个设置为例,我们研究了该方法背后的方法论及其工作原理。
原文链接:DLT相机标定算法 - BimAnt



















