【卷积神经网络】池化层【计算和python代码】

文章目录

1、简介
2、池化层计算
3、Stride
4、Padding
5、多通道池化计算
6、数学公式⭐
7、PyTorch 池化 API 使用
- 7.1、形状调整
- 7.2、最大和平均池化
- 7.3、调整stride步长
- 7.4、padding填充
- 7.5、多通道池化
- 7.6、完整代码⭐
8、小结

🍃作者介绍：双非本科大三网络工程专业在读，阿里云专家博主，专注于Java领域学习，擅长web应用开发、数据结构和算法，初步涉猎人工智能和前端开发。
🦅个人主页：@逐梦苍穹
📕所属专栏：人工智能
🌻gitee地址：xzl的人工智能代码仓库
✈ 您的一键三连，是我创作的最大动力🌹

1、简介

卷积层复习链接：https://xzl-tech.blog.csdn.net/article/details/140861325

池化层（Pooling Layer）是卷积神经网络（CNN）中的一种常用操作，用于减少特征图的尺寸，同时保留重要的空间信息。常见的池化操作包括最大池化（Max Pooling）和平均池化（Average Pooling）。
池化层的作用：

降维：通过池化操作，可以减少特征图的尺寸，从而降低计算量和存储需求。
防止过拟合：通过降维和降噪，池化层可以减少模型的复杂度，有助于防止过拟合。
不变性：池化操作可以引入平移不变性，即特征的位置轻微变化不会影响最终的分类结果。

最大池化和平均池化：

最大池化（Max Pooling）：从池化窗口中选择最大值。
平均池化（Average Pooling）：从池化窗口中计算平均值。

总结：

池化层 (Pooling) 降低维度，缩减模型大小，提高计算速度。
即：主要对卷积层学习到的特征图进行下采样（SubSampling）处理

2、池化层计算

最大池化：

max(0, 1, 3, 4)
max(1, 2, 4, 5)
max(3, 4, 6, 7)
max(4, 5, 7, 8)

平均池化：

mean(0, 1, 3, 4)
mean(1, 2, 4, 5)
mean(3, 4, 6, 7)
mean(4, 5, 7, 8)

3、Stride

最大池化：

max(0, 1, 4, 5)
max(2, 3, 6, 7)
max(8, 9, 12, 13)
max(10, 11, 14, 15)

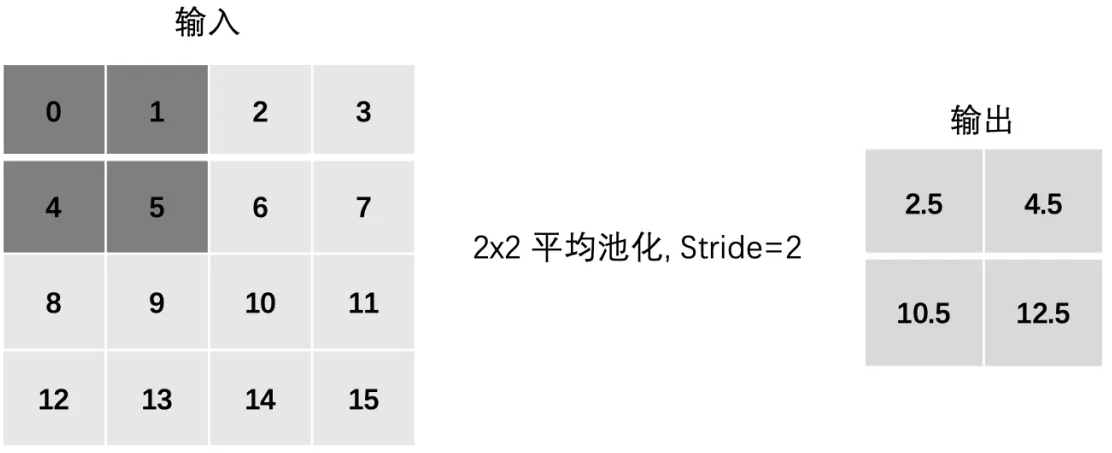
平均池化：

mean(0, 1, 4, 5)
mean(2, 3, 6, 7)
mean(8, 9, 12, 13)
mean(10, 11, 14, 15)

4、Padding

最大池化：

max(0, 0, 0, 0)
max(0, 0, 0, 1)
max(0, 0, 1, 2)
max(0, 0, 2, 0)
… 以此类推

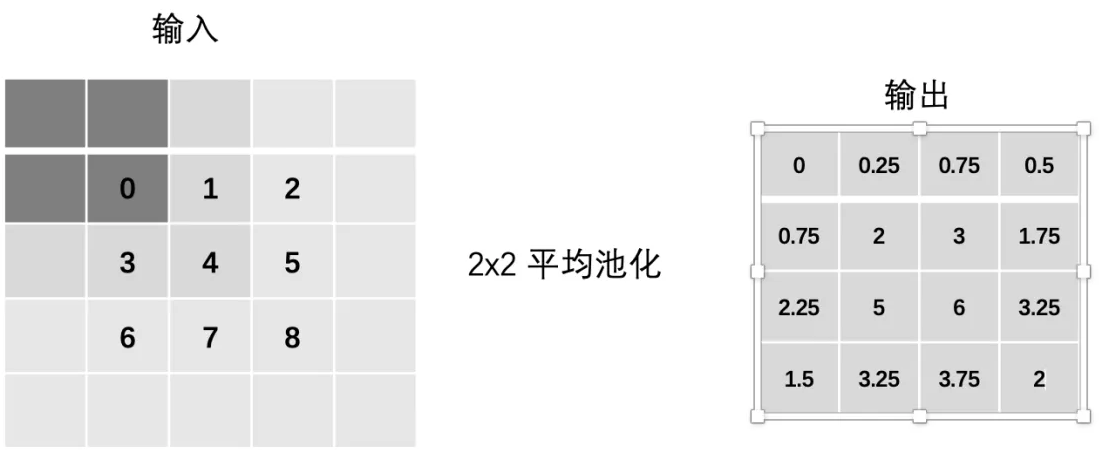
平均池化：

mean(0, 0, 0, 0)
mean(0, 0, 0, 1)
mean(0, 0, 1, 2)
mean(0, 0, 2, 0)
… 以此类推

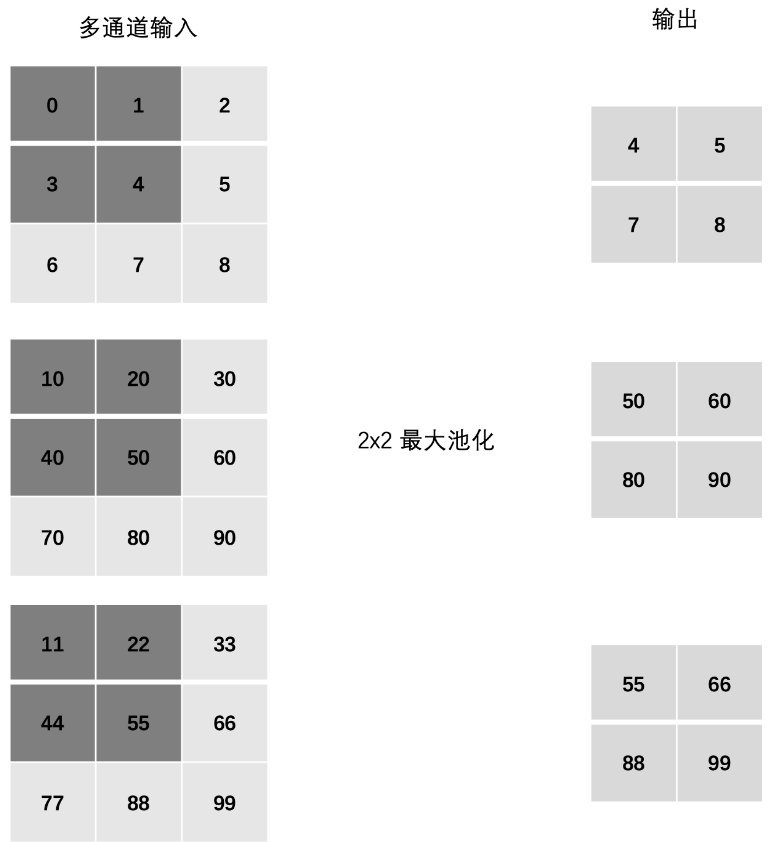
5、多通道池化计算

在处理多通道输入数据时，池化层对每个输入通道分别池化，而不是像卷积层那样将各个通道的输入相加。这意味着池化层的输出和输入的通道数是相等。

6、数学公式⭐

池化层的计算涉及池化窗口的大小、步幅和填充方式。下面是池化层计算的公式和示例。
假设输入特征图的尺寸为 $\times W$ ，池化窗口的大小为 $\times F$ ，步幅为 $S$ ，填充为 $P$ ，则输出特征图的大小为 $H_{\text{out}} \times W_{\text{out}}$ ，计算公式如下：
$H_{\text{out}} = \left\lfloor \frac{H - F + 2P}{S} \right\rfloor + 1$
$W_{\text{out}} = \left\lfloor \frac{W - F + 2P}{S} \right\rfloor + 1$
示例：
假设输入特征图的大小为 $\times 6$ ，池化窗口的大小为 $\times 2$ ，步幅为 $2$ ，没有填充（即 $P = 0$ ）。则输出特征图的大小计算如下：
$H_{\text{out}} = \left\lfloor \frac{6 - 2 + 2 \cdot 0}{2} \right\rfloor + 1 = \left\lfloor \frac{4}{2} \right\rfloor + 1 = 3$
$W_{\text{out}} = \left\lfloor \frac{6 - 2 + 2 \cdot 0}{2} \right\rfloor + 1 = \left\lfloor \frac{4}{2} \right\rfloor + 1 = 3$
所以输出特征图的大小为 $\times 3$ 。

7、PyTorch 池化 API 使用

7.1、形状调整

调整后的张量形状为 (N, C, H, W)，其中：

N 表示批次大小（Batch Size），这里是 1。
C 表示通道数（Channels），这里是 1。
H 表示高度（Height），这里是 3。
W 表示宽度（Width），这里是 3。

为什么要进行这些调整？
在深度学习中，卷积层和池化层通常期望输入的张量形状为 (N, C, H, W)，以便能够处理批次和通道。
因此，我们需要将输入张量调整为适当的形状，以便将其输入到卷积层或池化层中进行处理。

7.2、最大和平均池化

代码：

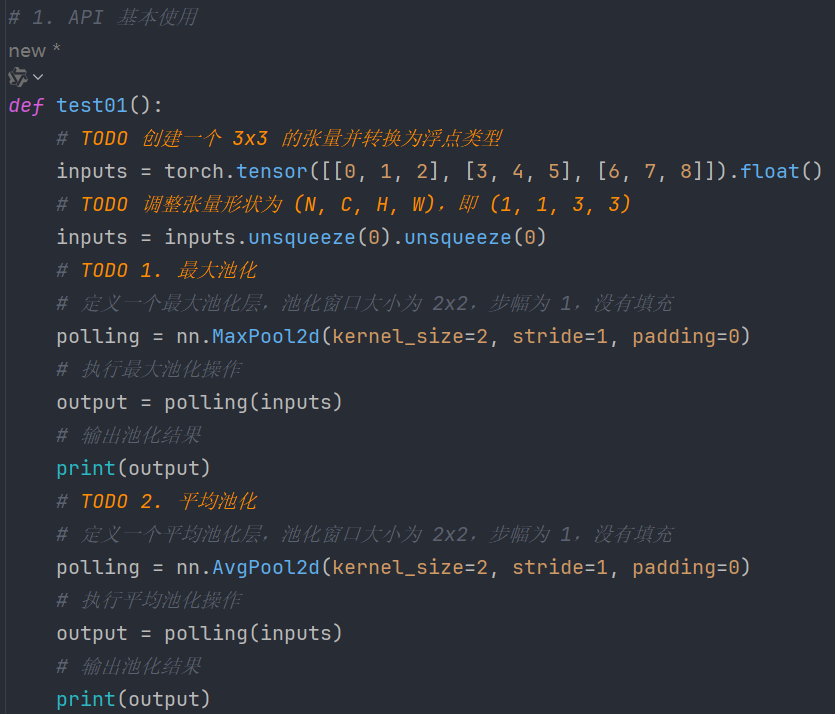
输出：

"C:\Program Files\Python39\python.exe" D:\Python\AI\神经网络\14、池化层.py 
tensor([[[[4., 5.],
          [7., 8.]]]])
tensor([[[[2., 3.],
          [5., 6.]]]])

Process finished with exit code 0

7.3、调整stride步长

代码：

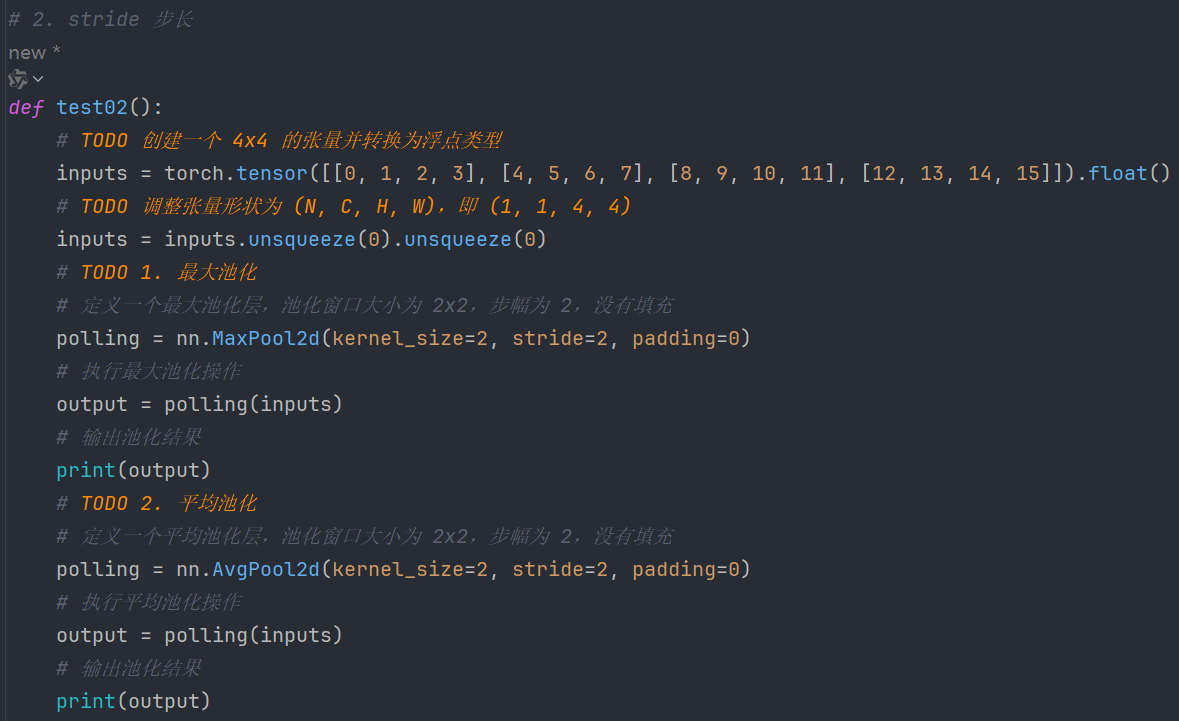
输出：

"C:\Program Files\Python39\python.exe" D:\Python\AI\神经网络\14、池化层.py 
tensor([[[[ 5.,  7.],
          [13., 15.]]]])
tensor([[[[ 2.5000,  4.5000],
          [10.5000, 12.5000]]]])

Process finished with exit code 0

7.4、padding填充

代码：

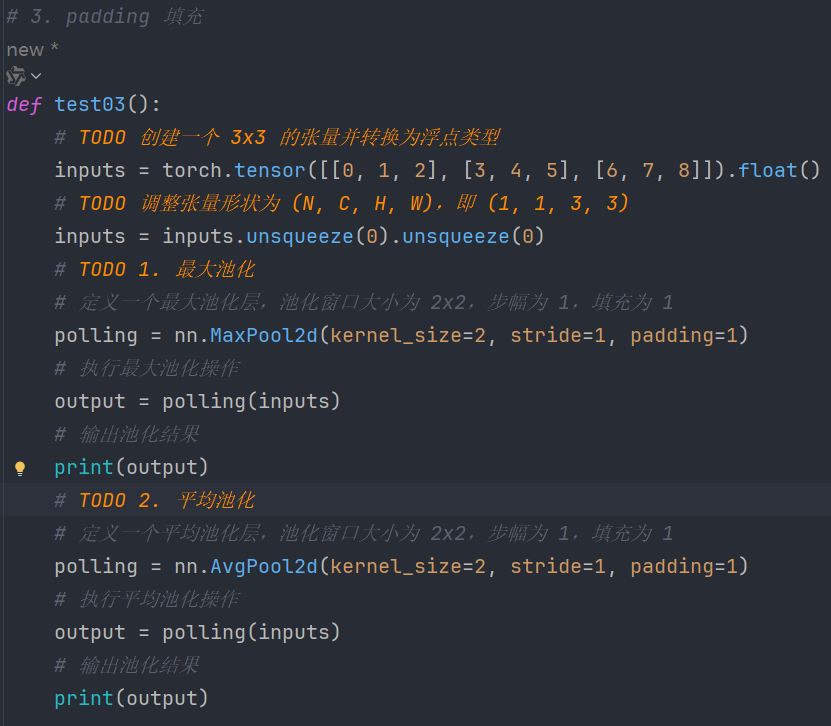
输出：

"C:\Program Files\Python39\python.exe" D:\Python\AI\神经网络\14、池化层.py 
tensor([[[[0., 1., 2., 2.],
          [3., 4., 5., 5.],
          [6., 7., 8., 8.],
          [6., 7., 8., 8.]]]])
tensor([[[[0.0000, 0.2500, 0.7500, 0.5000],
          [0.7500, 2.0000, 3.0000, 1.7500],
          [2.2500, 5.0000, 6.0000, 3.2500],
          [1.5000, 3.2500, 3.7500, 2.0000]]]])

Process finished with exit code 0

7.5、多通道池化

代码：

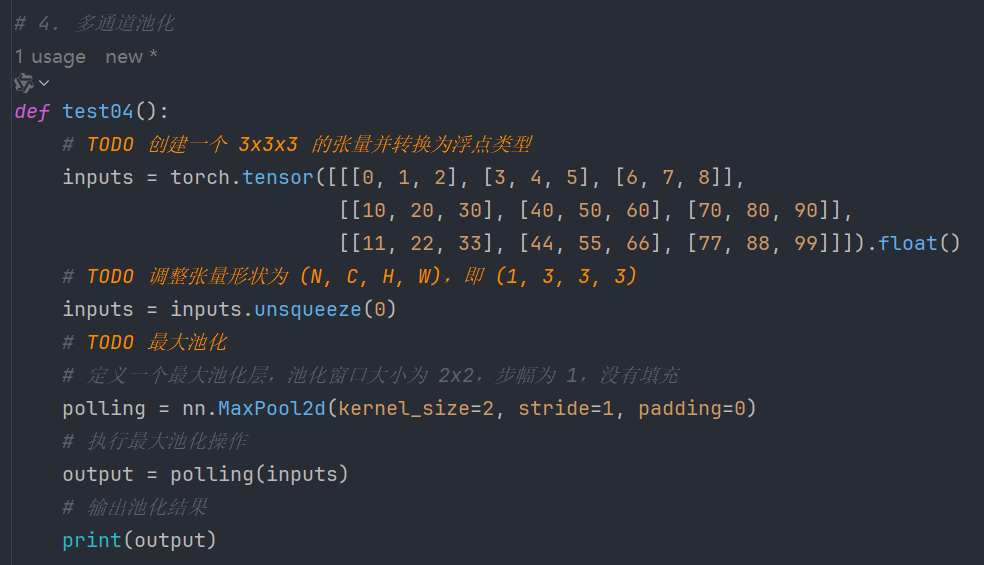
输出：

"C:\Program Files\Python39\python.exe" D:\Python\AI\神经网络\14、池化层.py 
tensor([[[[ 4.,  5.],
          [ 7.,  8.]],

         [[50., 60.],
          [80., 90.]],

         [[55., 66.],
          [88., 99.]]]])

Process finished with exit code 0

7.6、完整代码⭐

代码即注释：

# -*- coding: utf-8 -*-
# @Author: CSDN@逐梦苍穹
# @Time: 2024/8/2 3:42
import torch  # 导入 PyTorch 库，用于深度学习
import torch.nn as nn  # 导入 PyTorch 的神经网络模块


# 1. API 基本使用
def test01():
    # TODO 创建一个 3x3 的张量并转换为浮点类型
    inputs = torch.tensor([[0, 1, 2], [3, 4, 5], [6, 7, 8]]).float()
    # TODO 调整张量形状为 (N, C, H, W)，即 (1, 1, 3, 3)
    inputs = inputs.unsqueeze(0).unsqueeze(0)
    # TODO 1. 最大池化
    # 定义一个最大池化层，池化窗口大小为 2x2，步幅为 1，没有填充
    polling = nn.MaxPool2d(kernel_size=2, stride=1, padding=0)
    # 执行最大池化操作
    output = polling(inputs)
    # 输出池化结果
    print(output)
    # TODO 2. 平均池化
    # 定义一个平均池化层，池化窗口大小为 2x2，步幅为 1，没有填充
    polling = nn.AvgPool2d(kernel_size=2, stride=1, padding=0)
    # 执行平均池化操作
    output = polling(inputs)
    # 输出池化结果
    print(output)


# 2. stride 步长
def test02():
    # TODO 创建一个 4x4 的张量并转换为浮点类型
    inputs = torch.tensor([[0, 1, 2, 3], [4, 5, 6, 7], [8, 9, 10, 11], [12, 13, 14, 15]]).float()
    # TODO 调整张量形状为 (N, C, H, W)，即 (1, 1, 4, 4)
    inputs = inputs.unsqueeze(0).unsqueeze(0)
    # TODO 1. 最大池化
    # 定义一个最大池化层，池化窗口大小为 2x2，步幅为 2，没有填充
    polling = nn.MaxPool2d(kernel_size=2, stride=2, padding=0)
    # 执行最大池化操作
    output = polling(inputs)
    # 输出池化结果
    print(output)
    # TODO 2. 平均池化
    # 定义一个平均池化层，池化窗口大小为 2x2，步幅为 2，没有填充
    polling = nn.AvgPool2d(kernel_size=2, stride=2, padding=0)
    # 执行平均池化操作
    output = polling(inputs)
    # 输出池化结果
    print(output)


# 3. padding 填充
def test03():
    # TODO 创建一个 3x3 的张量并转换为浮点类型
    inputs = torch.tensor([[0, 1, 2], [3, 4, 5], [6, 7, 8]]).float()
    # TODO 调整张量形状为 (N, C, H, W)，即 (1, 1, 3, 3)
    inputs = inputs.unsqueeze(0).unsqueeze(0)
    # TODO 1. 最大池化
    # 定义一个最大池化层，池化窗口大小为 2x2，步幅为 1，填充为 1
    polling = nn.MaxPool2d(kernel_size=2, stride=1, padding=1)
    # 执行最大池化操作
    output = polling(inputs)
    # 输出池化结果
    print(output)
    # TODO 2. 平均池化
    # 定义一个平均池化层，池化窗口大小为 2x2，步幅为 1，填充为 1
    polling = nn.AvgPool2d(kernel_size=2, stride=1, padding=1)
    # 执行平均池化操作
    output = polling(inputs)
    # 输出池化结果
    print(output)


# 4. 多通道池化
def test04():
    # TODO 创建一个 3x3x3 的张量并转换为浮点类型
    inputs = torch.tensor([[[0, 1, 2], [3, 4, 5], [6, 7, 8]],
                           [[10, 20, 30], [40, 50, 60], [70, 80, 90]],
                           [[11, 22, 33], [44, 55, 66], [77, 88, 99]]]).float()
    # TODO 调整张量形状为 (N, C, H, W)，即 (1, 3, 3, 3)
    inputs = inputs.unsqueeze(0)
    # TODO 最大池化
    # 定义一个最大池化层，池化窗口大小为 2x2，步幅为 1，没有填充
    polling = nn.MaxPool2d(kernel_size=2, stride=1, padding=0)
    # 执行最大池化操作
    output = polling(inputs)
    # 输出池化结果
    print(output)


# 主程序入口
if __name__ == '__main__':
    test01()  # 运行最大池化测试
    test02()  # 运行平均池化测试
    test03()  # 运行填充测试
    test04()  # 运行多通道池化测试