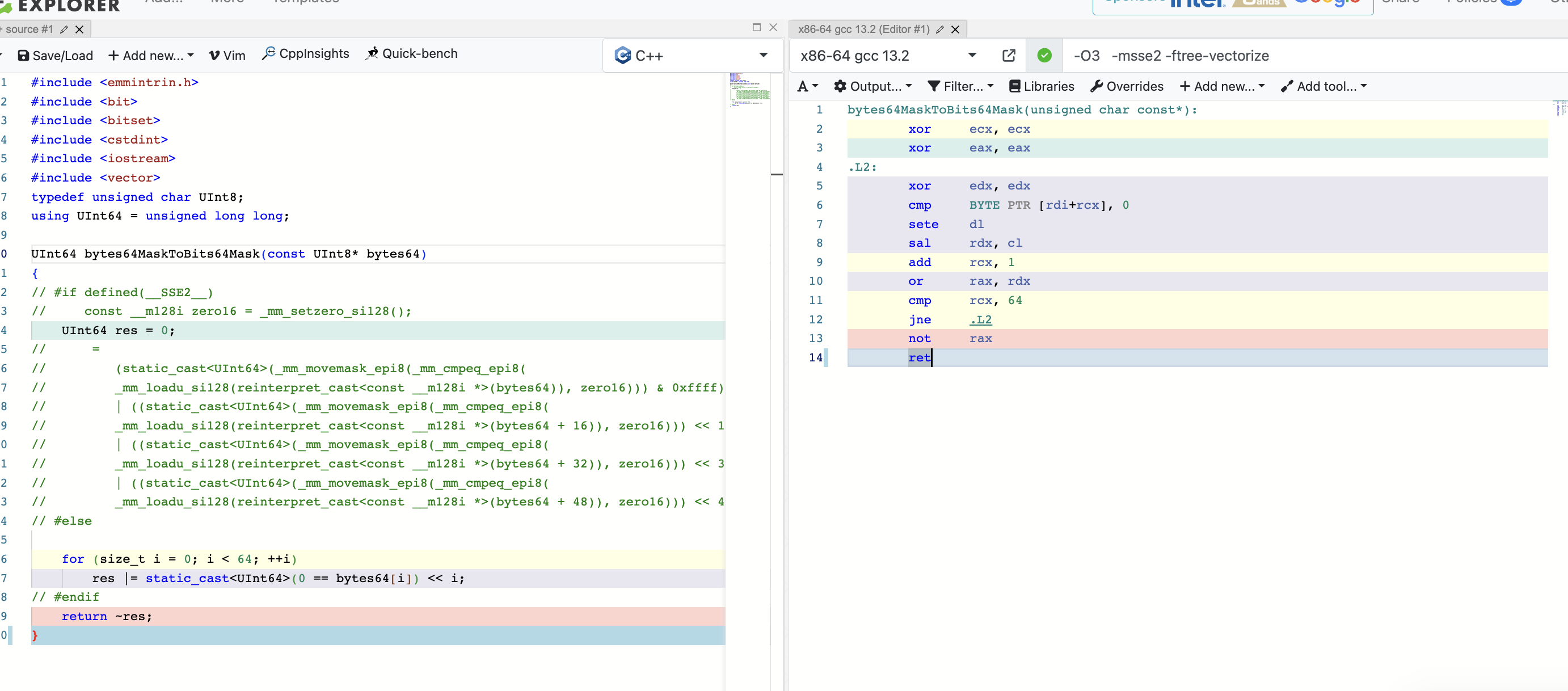
离散数学
- Proposition
- Ex 1:
- Ex 2:
- Ex 3:
- Ex 4:
- Ex 5:
- Ex 6:
- Ex 7:
- Ex 8:
Proposition
In mathematics, we have a mathematical proof is a verification of a proposition by a chain of logical deductions from a set of axioms.
在数学中,数学证明是通过一组公理的一系列逻辑演绎来验证一个命题。
Def: A proposition is a statement that is either True or False.
Ex 1:
2 + 3 = 5 2 + 3 = 5 2+3=5
Ex 2:
∀
n
∈
N
,
p
=
n
2
+
n
+
41
\forall n \in N, p = n^2 + n + 41
∀n∈N,p=n2+n+41
p is a prime number.
N = {0,1,2,3,…}, Natural numbers
'p is a prime number ’ is a predicate(断言)
a predicate is a proposition whose truth depends one the value of a variable – in this case n.
if n = {0,1,2,3,…,39} p is prime
but
if n = 40, then 40 * 40 + 40 + 41 = 41 * 41, not a prime
if n = 41, then 41 * 41 + 41 + 41 = 41 * 43, not a prime
Ex 3:
a
4
+
b
4
+
c
4
=
d
4
a^4 + b^4 + c^4 = d^4
a4+b4+c4=d4
has no positive integer solutions.
Now, this proposition was conjectured to be true by Euler in 1769.
Euler’s a big honcho in math, It was unsolved for over 2 centuries.Mathematicians worked on it. It was finally disapproved by a very clever fellow named Noam Elkies 218 years later after it was conjectured. And he came up with this:
a = 95800
b = 217519
c = 414560
d = 422481

∴ ∃ a , b , c , d ∈ N + , a 4 + b 4 + c 4 = d 4 \therefore \exist a,b,c,d \in N^+, a^4 + b^4 + c^4 = d^4 ∴∃a,b,c,d∈N+,a4+b4+c4=d4
It took a long time to figure out that actually there was a solution here. Obviously, everything they tried until that time failed. Let me give you another one.
Ex 4:
313
(
x
3
+
y
3
)
=
z
3
313(x^3 + y^3) = z^3
313(x3+y3)=z3
has no positive integer solutions.
it’s false.
This equation is an example of what’s called an elliptic curve.You study these if you’re really a specialist in mathematics in graduate school, or if you work for certain three-letter agencies, because it’s central to the understanding of how to factor large integers.Ok who cares about factoring? Well, factoring is the way to break crypto systems like RSA, which are used for everything that we do electronically today. You have a PayPal account. You buy something online. You’re using SSL. They’re all using crypto systems, almost all of which are based on number theory. And in particular, they’re based on factoring. And if you can find good asolutions to things like this, or solutions to things likes this, all of a sudden, you can get an angle and a wedge on factoring. And it’s because of that that now RSA uses 1,000 digits modulus’s instead of hundred digit modulus’s like they used to use, because people figured out how to factor and how to break the crypto system. If you could break those crypto systems, well, you can’t rule the world, but it’s close.
Ex 5:
The regions in any map can be colored in four colors, so that adjacent regions have different colors.It has a long history.It was conjectured by somebody named Guthrie in 1853. He’s the first person to say this ought to be possible. And there were many false proofs over the ensuing century. One of the most convincing was a proof using pictures by Kempe in 1879, 26 years later. And this proof was believed for over a decade. until another mathematician named Heawood found a fatal flaw in the argument. Now, this proof by Kempe consisted of drawing pictures of what maps have to look like. So he started by saying, a map has to look like one of these types. And he would draw pictures of them. And then he argued that those types that he draw pictures of, it worked for. Proofs by picture are often very convincing and very wrong. And the point will to be to show you proofs by picture are generally not a good thing. Because your brain just locks in-- oh, that’s what it has to look like. And you don’t think about other ways that it might look like. Now, the four color theorem was finally proved by Appel and Taken in 1977, but they had to use a computer to check thousands of cases. Now, this was a little disturbing to mathematicians, because how do they know the computer didi the right thing? Your colleague writes a proof on the board. You can check it,. But how do you know the computer didn’t mess up, or not do some cases? Now, everybody believes it’s true now. But it’s unsatisfying.
Ex 6:
Every even integer but 2, actually, positive integer but 2, is the sum of two primes. For example, 24 is the sum of 11 and 13, which are prime.
Nobody knows if this is true or false. This is called Goldbach’s conjecture. It was conjectured by Christian Goldbach in 1742. This is a really simple proposition. And it’s amazing it’s not known.
Ex 7:
∀ n ∈ Z , n ≥ 2 ⟹ n 2 ≥ 4 \forall n \in Z, n \ge 2 \implies n^2 \ge 4 ∀n∈Z,n≥2⟹n2≥4
Def: An implication p implies q is said to be true if p is false or q is true, either one. So we can write this down in terms of a truth table as follows. You have the values of p and q. And I’ll give the value of p implies q. If p is true and q is true, what about p implies q? It’s true, because q is true in the definition. If p is true and q is false? p implies q is False. if p is false q is true, p implies q is True. What about false and false? p implies q is True. So this is important to remember. False implies anything is True, which is a little strange. There’s a famous expression. If pigs could fly, I would be king. Sort of. In fact, this statement, pigs fly implies I’m king-- that’s true, because pigs don’t fly. Doesn’t matter whether or not I’m king, which I’m not.Since pigs don’t fly, even though that’s false, the implication is true.
Ex 8:
∀
n
∈
Z
,
n
≥
2
⟺
n
2
≥
4
\forall n \in Z, n \ge 2 \iff n^2 \ge 4
∀n∈Z,n≥2⟺n2≥4
that is False, for example: n = -3
Truth Table:
| p | q | p => q | q => p | p <=>q |
|---|---|---|---|---|
| T | T | T | T | T |
| T | F | F | T | F |
| F | T | T | F | F |
| F | F | T | T | T |