一、算法简介
简单地说,Alphazero=MCTS + SL(策略网络+价值网络) +Selfplay + resnet。 其中MCTS指的是蒙特卡洛树搜索,主要用于记录所有访问过的棋盘状态的各种属性,包括该状态访问次数,对该状平均评价分数等。 SL指监督学习算法,监督网络输出价值v和策略pai,用于拟合mcts推测出的策略和价值,并泛化到未见过的状态上。 Selfplay是一种训练方法,步骤是:实例化蒙特卡罗树和SL网络,进行自我博弈,以产生多样化的数据进行训练和更新。 resnet 众所周知是一种卷积神经网络,主要用于棋盘的特征提取。下面从采样和更新两个角度对上述几个部件进行介绍。文中所引代码来自alphazero GitHub 五子棋
1、蒙特卡洛树搜索
顾名思义,蒙特卡洛树搜索是一种利用树形数据结构进行搜索的算法,其节点存储是棋盘状态,根节点存储的是棋盘初始状态,其子节点存储是当前状态可能的下一状态。节点上存储的属性包括棋盘当前棋子位置s,访问s的次数n,对节点的估值v。
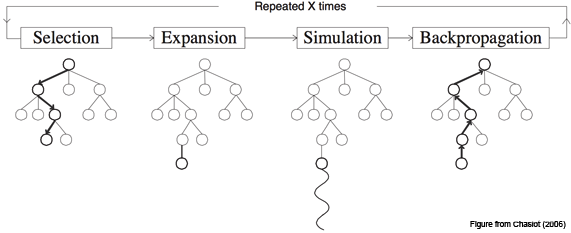
图一、蒙特卡洛树搜索的采样和更新(select, expand, simulate为采样,backpropagate为更新)
1.1 MCTS采样
mcts(蒙特卡洛树搜索)的采样分为三步:节点选择,节点拓展,和模拟推演。三步是依次执行的。
1.节点选择:初始化根节点,从根节点开始,对所有可能的子节点计算puct值,选择值最大的进入,puct计算公式如下
其中vi 是该节点的价值,N是父节点被访问次数,ni为本节点被访问的次数,C为超参数用于平衡利用和探索。
2.节点扩展:如果当前节点已经是树的叶子节点,则需对树进行节点扩展,具体步骤为:从可能的动作中选取一个执行,进入下一状态,并将这个新节点加入到父节点的子节点集中。
3.模拟推演:在将一个新节点加入树后,需要从这个节点的状态出发(如果此节点非终止状态),进行模拟推演,直至到达种植状态。在模拟中,不适用树来做决策,而是使用强化学习的actor和critic网络做决策。
1.2 MCTS更新
1. 反向回溯: 在模拟对局进行到终局状态后,一般会有胜负和的情况,记胜利的结局价值为1 失败的结局价值为-1,从叶子节点开始一次反溯其父节点,将沿途每个节点的访问次数+1,总价值加上新的结局价值,并用新的总价值除以访问次数得到平均价值。反向传播就是利用此次胜负结果,从这次推演的叶子节点开始,迭代查询出所有的父节点,并更新这些父节点上的价值估值vi 。
实际Alphazero算法中使用的mcts细节比上面描述的有所不同,在第三节算法流程中介绍
2、策略网络和价值网络
采样:在mcts采样到达第三步模拟推演时,开始使用策略网络和价值网络推演,从当前状态s开始,每次选择一动作a执行,直至到达终点获得胜负结果。
更新:这里需要注意,虽然网络结构用了策略网络和状态价值网络形式建模,但是其损失函数完全不同于actor critic的loss。actor critic 使用的是强化学习中的策略梯度损失和td error进行更新。而alphazero中的策略网络和价值网络更新方式是监督学习的方法,策略网络使用交叉熵损失,求网络输出策略和节点统计策略的差异。 价值网络使用均方差损失,求网络输出价值和节点monte carlo方法统计的价值均值之间的损失。【蒙特卡洛本身就是一种通过采样拟合近似计算问题的解或者概率分布,所以不能因为其带有策略和价值网络就默认用actor和critic的思想去理解,那就错了】
更新方式:价值网络和策略网络的输入是棋局推演中每一step的state,价值网络输出每一state的预估价值【范围[-1,1]】其label是该局最终的胜负情况,胜则+1,负则-1。策略网络输出的是每一state下采取的策略的概率分布,其标签为,使用的是均方差误差做回归损失,而policy的标签使用的是mcts推导出的策略分布,使用的是交叉熵损失做分类的损失。两项损失的和是网络的总损失

3.SelfPlay
selfplay 即使用模型和自己对战,因为模型在学习和变化,所以可以产生不同分布的数据,相比于alphago的对棋谱训练增加数据多样性,增强了泛化性。
alphazero要使用 mcts和sl 完成自博弈的过程,就需要mcts和sl 既可以输出先手的策略,也可以输出后手的策略。为实现这一点,mcts采取的方式是,在节点价值从叶子节点向根节点迭代更新时,每一次都传入 -value,即相邻两节点估值符号相反,这样使得每一个节点上的估值都是当前player对棋局的估值。 sl中的value和policy因为是学习拟合mcts的输出,所以其也具有了输出先后手策略和价值的能力。
二、算法整体流程介绍
整体伪代码如下
初始化价值网络 V 和策略网络 pi
对于 i 在范围 1500 内循环:
# 通过自对弈收集数据
环境重置()
初始化根节点
当未完成时循环:
动作, 动作概率 = 玩家获取动作()
# 通常在 get_action 函数中涉及 400 次选择和扩展。
# 如果任何一次迭代达到游戏结束,更新 MCTS 节点的值。
当前状态 = 下一状态
将根节点移至当前状态的节点
如果收集到的数据 > 批量大小:
使用收集到的数据训练策略网络和价值网络