内容介绍
给定一个 n × n 的二维矩阵
matrix表示一个图像。请你将图像顺时针旋转 90 度。你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[[7,4,1],[8,5,2],[9,6,3]]示例 2:
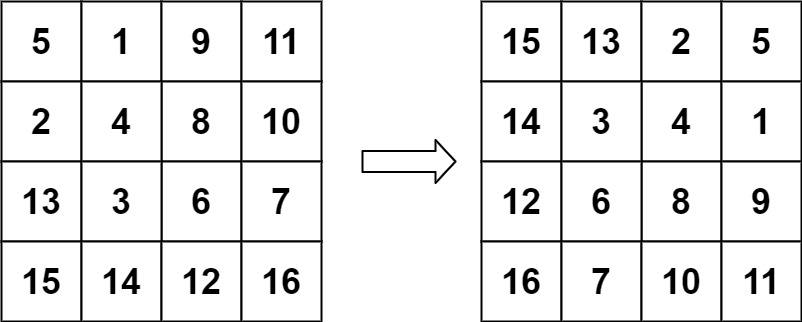
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] 输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]提示:
n == matrix.length == matrix[i].length1 <= n <= 20-1000 <= matrix[i][j] <= 1000
完整代码
void rotate(int** matrix, int matrixSize, int* matrixColSize) {
int matrix_new[matrixSize][matrixSize];
for (int i = 0; i < matrixSize; i++) {
for (int j = 0; j < matrixSize; j++) {
matrix_new[i][j] = matrix[i][j];
}
}
for (int i = 0; i < matrixSize; ++i) {
for (int j = 0; j < matrixSize; ++j) {
matrix[j][matrixSize - i - 1] = matrix_new[i][j];
}
}
}
思路详解
这段代码实现了将一个二维矩阵顺时针旋转90度的功能。以下是详细步骤和思路:
1. 创建新矩阵
int matrix_new[matrixSize][matrixSize];
- 首先定义一个新的二维数组
matrix_new,其大小与输入矩阵matrix相同。这个新矩阵用于暂时存储原矩阵的值,以避免在旋转过程中覆盖原数据。
2. 复制原矩阵到新矩阵
for (int i = 0; i < matrixSize; i++) {
for (int j = 0; j < matrixSize; j++) {
matrix_new[i][j] = matrix[i][j];
}
}
- 通过两层嵌套循环,将原矩阵
matrix中的每个元素复制到新矩阵matrix_new中对应的索引位置。这一步确保了在旋转操作过程中,原矩阵的数据不会丢失。
3. 旋转矩阵
for (int i = 0; i < matrixSize; ++i) {
for (int j = 0; j < matrixSize; ++j) {
matrix[j][matrixSize - i - 1] = matrix_new[i][j];
}
}
- 再次使用两层嵌套循环来执行旋转操作。对于新矩阵
matrix_new中的每个元素matrix_new[i][j],将其放置到原矩阵matrix的matrix[j][matrixSize - i - 1]位置。 - 这里,
matrix[j][matrixSize - i - 1]的计算是基于以下观察:- 原矩阵中的行
i将变成旋转后矩阵的列j。 - 原矩阵中的列
j将变成旋转后矩阵的行matrixSize - i - 1。这是因为旋转90度后,原矩阵的最后一列变成了新矩阵的第一行,第二列变成了第二行,以此类推。
- 原矩阵中的行
4. 完成旋转
- 经过上述步骤后,原矩阵
matrix中的元素已经被顺时针旋转了90度,无需返回值,因为旋转是在原地进行,直接修改了输入矩阵。
代码亮点
- 原地操作:该算法直接在输入矩阵上进行操作,节省了额外的空间。
- 直观的旋转逻辑:通过简单的索引变换,实现了矩阵的旋转,易于理解和实现。
注意事项
- 代码中使用了固定大小的数组
matrix_new,这在C语言中是合法的,但限制了函数的可重用性。如果矩阵大小在编译时未知,应使用动态内存分配。 - 该算法假定输入矩阵是正方形的,即行数和列数相等。如果矩阵不是正方形,代码需要相应调整。
知识点精炼
-
矩阵复制:
- 使用嵌套循环将原矩阵的元素复制到一个新矩阵中,以保持原始数据。
-
索引变换:
- 利用索引变换公式
matrix[j][matrixSize - i - 1]将新矩阵的元素放置到原矩阵的旋转位置。
- 利用索引变换公式
-
原地操作:
- 直接在原矩阵上进行旋转操作,无需额外的存储空间。
-
嵌套循环:
- 使用两层嵌套循环遍历矩阵的行和列。
-
数组初始化:
- 在栈上静态分配一个二维数组
matrix_new用于暂存数据。
- 在栈上静态分配一个二维数组
-
矩阵性质:
- 理解矩阵旋转90度后的行与列的对应关系。
-
边界条件:
- 在索引变换中,确保访问矩阵的合法位置,避免越界。
-
空间复杂度:
- 算法的空间复杂度为O(n^2),其中n是矩阵的行数或列数。
-
时间复杂度:
- 算法的时间复杂度为O(n^2),因为每个元素都需要被访问和赋值一次。
-
算法通用性:
- 算法仅适用于正方形矩阵,对于非正方形矩阵需要调整。
应用场景
图像处理
- 图像旋转:在图像编辑软件中,用户经常需要旋转图片。矩阵旋转算法可以用来实现这一功能,将图像像素按照一定角度旋转。
- 视频处理:视频帧也可以视为矩阵,旋转算法可用于视频编辑中的帧旋转。
2. 计算机图形学
- 物体旋转:在3D图形渲染中,物体在空间中的旋转可以通过矩阵旋转来实现。
- 视角变换:在图形学中,通过旋转矩阵来改变视角,实现从不同角度观察3D模型。
3. 机器人学和自动化
- 路径规划:在机器人导航中,矩阵旋转算法可以帮助调整坐标系,以便进行路径规划和避障。
- 传感器数据处理:某些传感器(如激光雷达)的数据可以表示为矩阵形式,旋转算法有助于处理这些数据。
4. 机器学习和数据分析
- 特征变换:在机器学习中,数据预处理可能涉及矩阵旋转,以改善模型的性能或适应特定算法的要求。
- 降维:在数据降维技术中,如主成分分析(PCA),矩阵旋转可以用来找到数据的主要方向。
5. 控制系统
- 状态空间表示:在控制理论中,系统的状态可以用矩阵表示,旋转算法可以用于状态变换。
6. 物理学和工程学
- 晶体学:在晶体学中,旋转矩阵用于描述晶体结构的对称性。
- 结构分析:在工程学中,分析结构的受力情况可能需要将坐标系旋转到某个特定的角度。
7. 日常应用
- 游戏开发:在游戏开发中,矩阵旋转用于实现角色和物体的旋转动画。
- 桌面应用:比如电子表格软件中的数据旋转,以不同的视角查看数据。