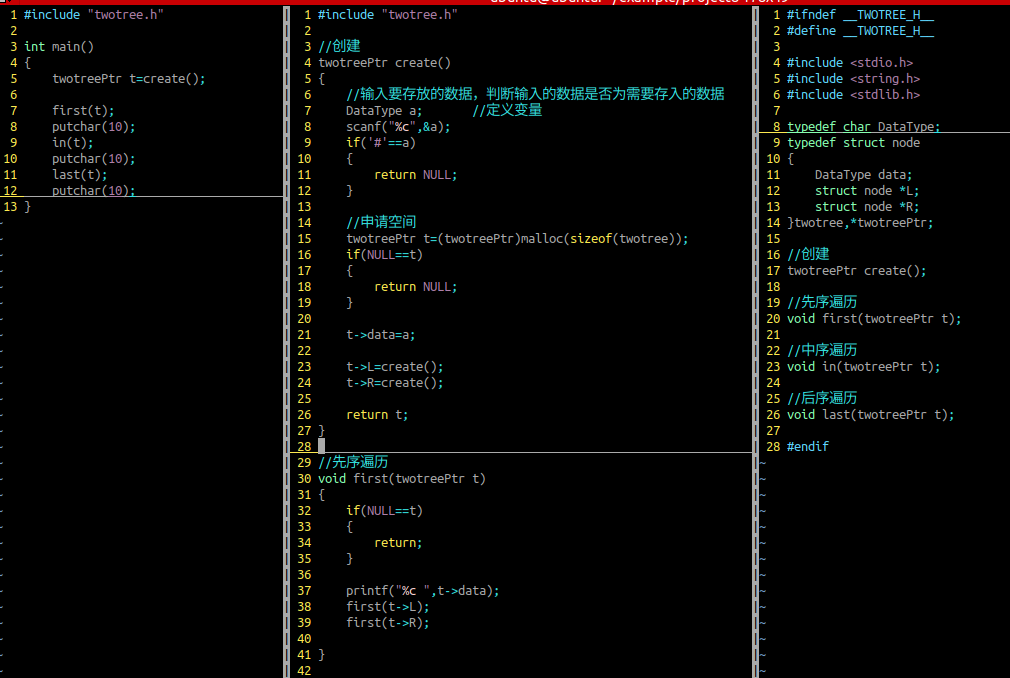
二叉树的存储
满二叉树或者完全二叉树可以采用顺序存储,普通二叉树一般采用链式存储
节点的结构体原型
typedef int DataType
typedef struct node
{
DataType data;
struct node *L;
struct node *R;
}twotree,*twotreePtr;
二叉树的相关操作(功能函数的封装)
创建
函数返回类型:二叉树指针
参数列表:无
判断申请空间是否合法
先序遍历
先打印数据,再打印左节点的数据,最后再打印右节点的数据
参数列表:二叉树指针
判断申请空间是否合法
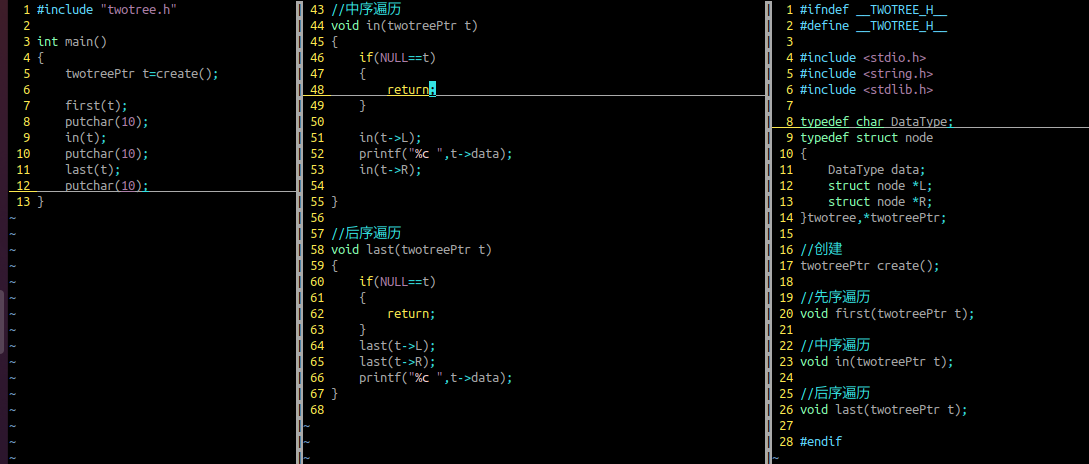
中序遍历
先打印左节点的数据,再打印数据,最后再打印右节点的数据
后序遍历
先打印左节点的数据,再打印右节点的数据,最后再打印数据
已知先序遍历和中序遍历的结果,反推二叉树
已知后序遍历和中序遍历的结果,反推二叉树
算法
概念
计算机解决问题的方法
特性
确定性:算法每一个语句具有确定的意思
有穷性:在执行一定时间后,自动结束算法
输入:至少有0个或多个输入
输出:至少有一个或多个输出
可行性:经济可行,社会可行
算法设计要求
正确性:对于正确的输入,会给出正确的结果,尽可能少的出现Bug
健壮性:对于错误的输入,要给出合理的处理
可读性:要求代码要有注释、有缩进、命名要规范
高效率:要求时间复杂度尽可能低
低存储:空间复杂度尽可能低
算法时间复杂度(T(n))
算法时间复杂度计算公式:T(n) = O(f(n));
T(n):时间复杂度
n:表示问题的规模
f(n) :是问题规模与执行次数之间的函数
O(f(n)):使用O阶记法,记录算法时间复杂度
时间复杂度推导

常见的时间复杂度
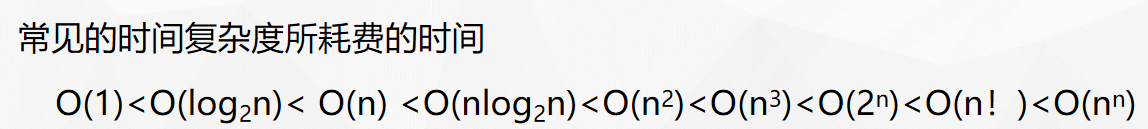
排序算法
概念
定义:将给定的序列,按照关键字进行升序或降序排列的过程叫做排序
分类:
交换类排序:冒泡排序、快速排序
选择类排序:简单选择排序,堆排序
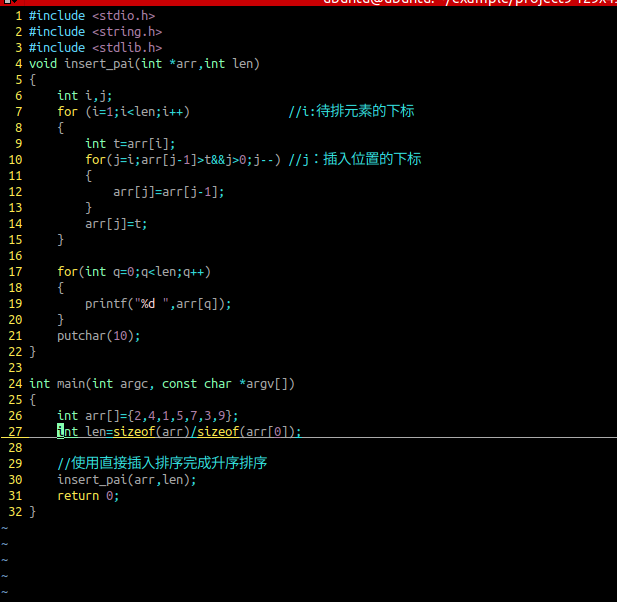
插入类排序:直接插入排序、折半插入排序、希尔排序
归并排序:二路归并、三路归并。。。
基数排序
快速排序
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
//定义一个基准
int get(int *p,int l,int r)
{
int q=p[l];
while(l<r)
{
while(p[r]>q&&l<r)
{
r--;
}
p[l]=p[r]; //将小的数据放左边
while(p[l]<q&&l<r)
{
l++;
}
p[r]=p[l]; //将大的数据放右边
}
p[l]=q;
return l;
}
//实现快速排序
void quick(int *p,int l,int r)
{
if(l<r)
{
int q=get(p,l,r);
quick(p,l,q-1);
quick(p,q+1,r);
}
}
void show(int *p,int len)
{
for(int i=0;i<len;i++)
{
printf("%d ",p[i]);
}
putchar(10);
}
int main(int argc, const char *argv[])
{
int arr[]={2,1,5,4,3,9,8};
int len=sizeof(arr)/sizeof(arr[0]);
//快速排序
quick(arr,0,len-1);
show(arr,len);
return 0;
}直接插入排序
查找算法
概念
按照关键字,在查找表中查询是否存在的算法叫做查找
分类
顺序查找:将给定的查找表进行全部遍历一遍,与要查找的关键字进行比对。
折半查找(二分查找):在顺序存储的有序序列中,通过进行逐次减半查找范围,查找特定的关键字的算法,叫做折半查找。
哈希查找:通过哈希函数,在哈希表中定位要找的数据元素
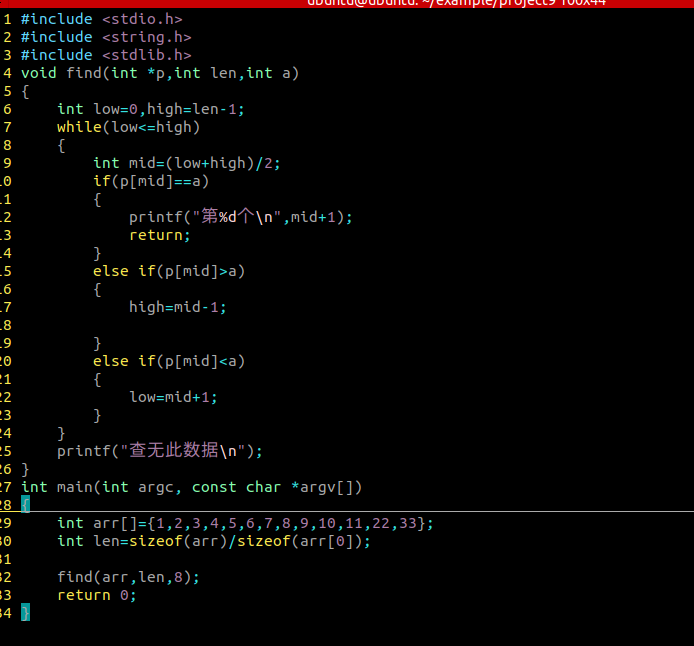
折半查找
要求:查找表是顺序存储,并且有序序列
原理:通过不断减半查找范围,最后确定查找的值
算法:
哈希查找
哈希表是借助哈希函数将序列存储于连续存储空间的查找表
哈希函数是根据关键字确定存储位置的函数
哈希函数的构造方式:直接定址法、数字分析法、平方取中法、折叠法、除留余数法、随机数法
哈希冲突是不同关键字由哈希函数得到相同存储位置的现象
解决哈希冲突的方法:
1、开放定址法
线性探测法
二次探测法
伪随机探测法
2、再哈希法
3、链地址法 (顺序表和链表的集合)
4、建立公共溢出区
哈希表的长度确定方法:数据元素个数除以四分之三得到的最大素数
哈希查找的完整实现
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
//哈希长度=存放元素的个数*4/3
#define N 13 //存放了10个元素,哈希长度为13
//定义一个哈希表的结构体原型
typedef struct node
{
int data;
struct node *next;
}hash,*hashPtr;
//哈希表的存储
void add(hashPtr h[],int data)
{
int idex=data%N;
//申请空间,封装数据
hashPtr p=(hashPtr)malloc(sizeof(hash));
if(NULL==p)
{
printf("申请失败\n");
return;
}
p->data=data;
p->next=NULL;
p->next=h[idex];
h[idex]=p;
}
//打印哈希表
void show(hashPtr h[],int len)
{
for(int i=0;i<len;i++)
{
printf("%d ",i);
hashPtr p=h[i];
while(p)
{
printf("%d ",p->data);
p=p->next;
}
printf("NULL\n");
}
}
//哈希查找
void find(hashPtr h[],int len,int data)
{
int idex=data%N;
hashPtr p=h[idex];
while(p)
{
if(p->data==data)
{
printf("FIND,%d\n",idex);
return;
}
printf("NO FIND\n");
}
}
int main(int argc, const char *argv[])
{
int arr[]={12,45,35,48,67,15,46,18,94,64};
int len=sizeof(arr)/sizeof(arr[0]);
//定义一个哈希表
hashPtr h[N];
//初始化哈希表
for(int i=0;i<len;i++)
{
h[i]=NULL;
}
//将数据存入哈希表
for(int i=0;i<len;i++)
{
add(h,arr[i]);
}
show(h,len);
find(h,len,18);
return 0;
}