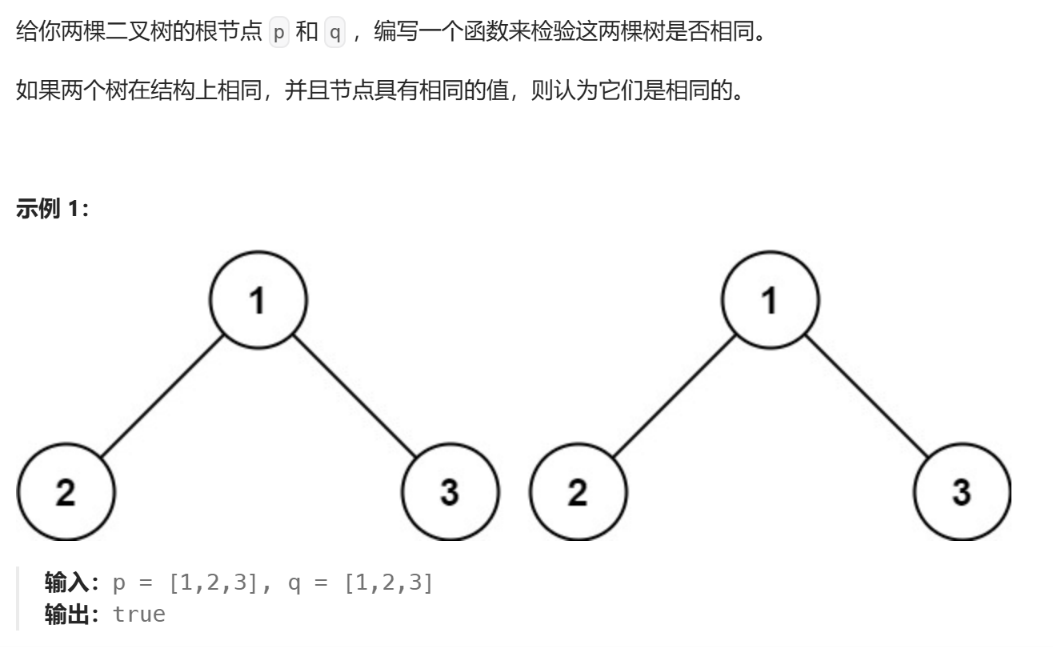
检查两棵树是否相同

100. 相同的树 - 力扣（LeetCode）

思路解透

---

1. 两个根节点一个为空一个不为空的话，这两棵树就一定不一样了
2. 若两个跟节点都为空，则这两棵树一样
3. 当两个节点都不为空时：
   1. 若两个根节点的值不相同，则这两棵树不一样
   2. 若两个跟节点的值相同，则对左右两棵子树进行递归判断

---

代码解析

/**  
 * 时间复杂度为：O(min(m,n))  
 * @param p  m个节点  
 * @param q  n个节点  
 * @return  
 */
public boolean isSameTree(TreeNode p, TreeNode q) {  
    //1. 一个为空，一个不为空，必不一样  
    if(p == null && q != null || p != null && q == null){  
        return false;  
    }    
    
    //2. 两个都为空  
    if(p == null && q == null){  
        return true;  
    }    
    
    //3. 剩下的一种情况就是两个都不为空，不需要再用if限制条件了  
    if(p.val != q.val){  
        return false;  
    }    
    
    //4. 此时代表两个都不为空，且 val 的值相等  
    //5. 说明根节点相同，系接下来判断两棵树的左右是不是同时分别相同  
    return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);  
}

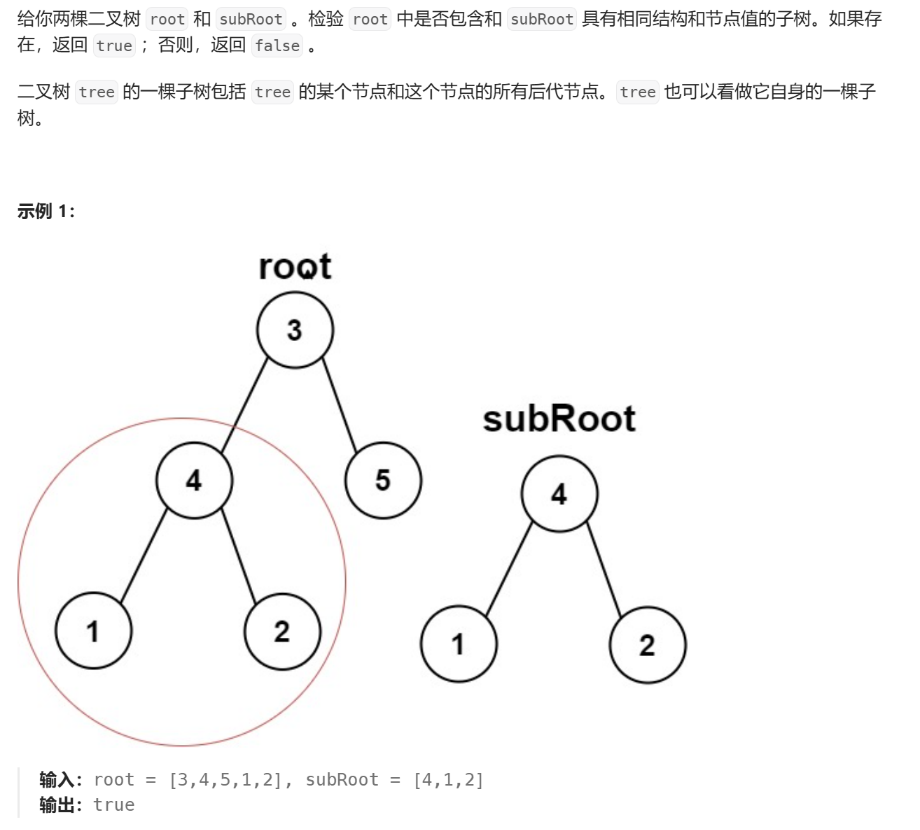
另一棵树的子树

572. 另一棵树的子树 - 力扣（LeetCode）

思路解透

---

注意： 当两棵树相同时，也返回 true

1. 首先判断两棵树是否相同，若相同，返回 true（需要调用上面一题的方法）
2. 若不相同，判断是否是左子树的子树，是否是右子树的子树
3. 若都不是，则返回 false

---

代码解析

/**  
 * 判断两棵树是否相同  
 * @param p  
 * @param q  
 * @return  
 */  
public boolean isSameTree(TreeNode p, TreeNode q){  
    if(p == null && q == null){  
        return true;  
    }    
    if(p != null && q == null || p == null && q != null){  
        return false;  
    }    
    //都不为空  
    if(p.val != q.val){  
        return false;  
    }    
    //对子树进行判断  
    return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);  
}  
  
/**  
 * 判断是不是子树  
 * 时间复杂度：O(m*n)  
 * @param root  
 * @param subRoot  
 * @return  
 */  
public boolean isSubtree(TreeNode root, TreeNode subRoot) {  
    if(root == null){  
        return false;  
    }    
    //1. 两棵树若相同
    if(isSameTree(root,subRoot)){  
        return true;  
    }    
    
    //2. 判断是否是左子树的子树
    if(isSubtree(root.left,subRoot)){  
        return true;  
    }    
	
	//3. 判断是否是右子树的子树
    if(isSubtree(root.right,subRoot)){  
        return true;  
    }    
    return false;  
}

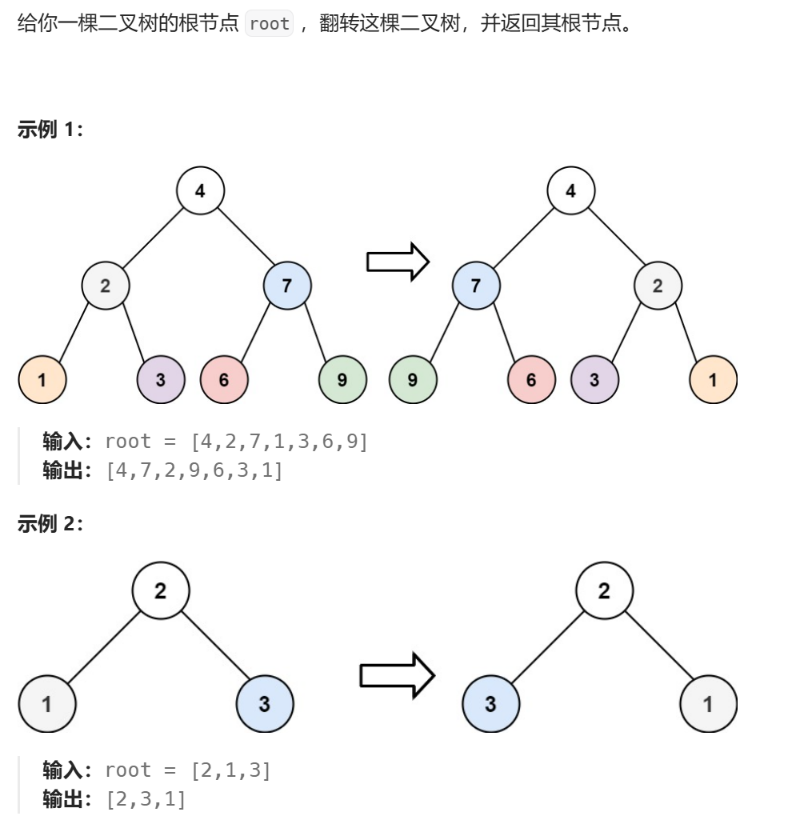
翻转二叉树

226. 翻转二叉树 - 力扣（LeetCode）

思路解透

---

1. 若跟节点为空就返回 null
2. （优化步骤）若左右两边都为空，就不需要交换了，直接返回 root
3. 定义一个 ret 节点作为中间人，将左右子节点进行交换
4. 递归对左右子节点的左右子节点进行交换
5. 返回 root

---

代码解析

/**  
 * 翻转二叉树  
 * @param root  
 * @return  
 */  
public TreeNode invertTree(TreeNode root) {  
    if(root == null) {  
        return null;  
    }    
    if(root.left == null && root.right == null){  
        return root;  
    }    
    //左右子节点进行交换
    TreeNode ret = root.right;  
    root.right = root.left;  
    root.left = ret;  
    
    invertTree(root.left);  
    invertTree(root.right);  
    
    return root;  
}

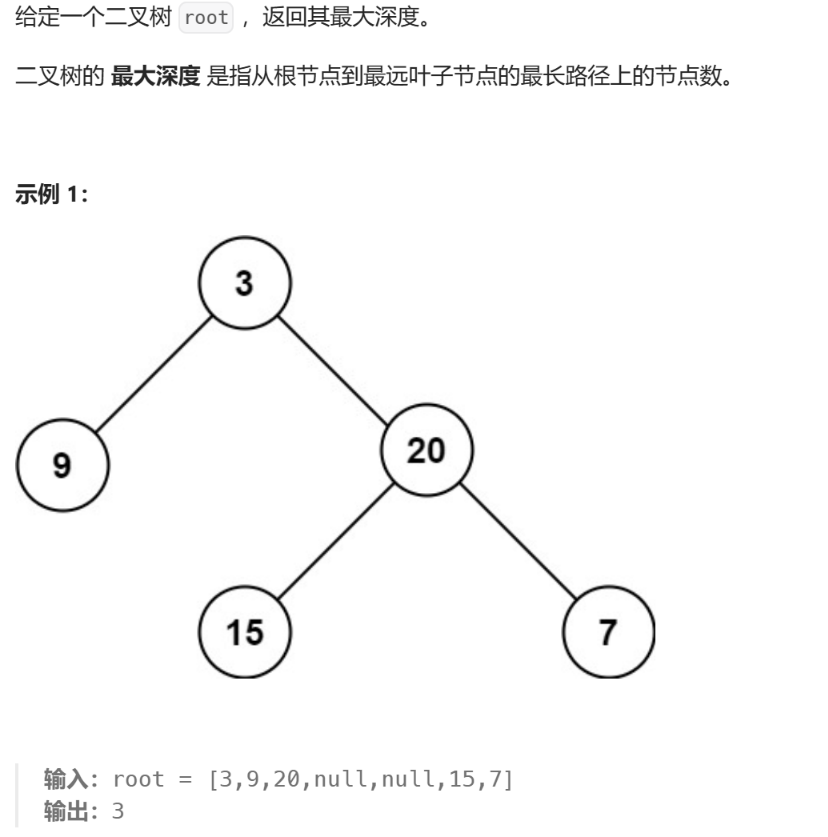
二叉树最大深度

104. 二叉树的最大深度 - 力扣（LeetCode）

思路解透

---

树的高度 = { 左树高度，右树高度 } m a x + 1 树的高度 = {\{左树高度，右树高度\}}_{max}+1 树的高度={左树高度，右树高度}max​+1
root 下来之后，每次都是取左右两边更高的那一个，再+1 递归上去

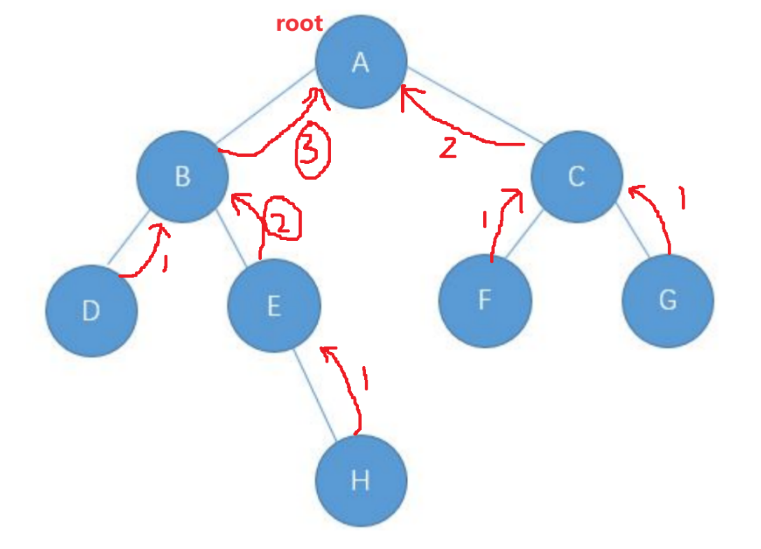
代码解析

//获取二叉树的高度  
public int maxDepth(TreeNode root) {  
    if(root == null){  
        return 0;  
    }    
    int leftDepth = maxDepth(root.left);  
    int rightDepth = maxDepth(root.right);  
    
    return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;  
}

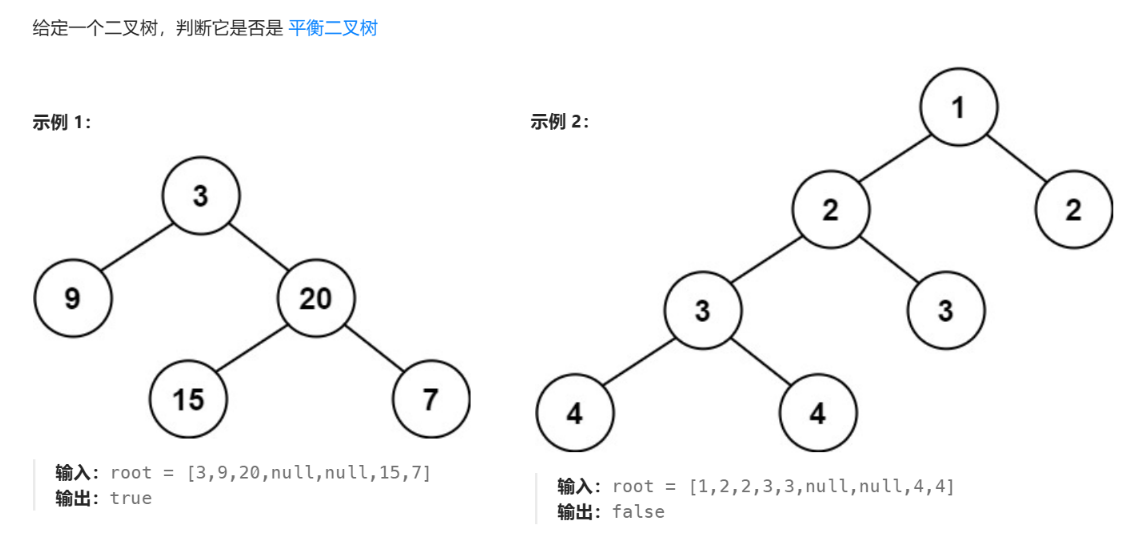
平衡二叉树

110. 平衡二叉树 - 力扣（LeetCode）

思路解透

平衡二叉树：
所有节点的左右子树高度差小于等于 1

1. 当前 root 的左右子树高度差小于等于 1
   • 用到 Math.abs() 方法，得到的是() 里面的绝对值
2. 同时满足 root 的左子树平衡 && root 的右子树平衡

---

代码解析

/**  
 * 获取最大深度  
 * @param root  
 * @return  
 */  
public int maxDepth(TreeNode root) {  
    if(root == null){  
        return 0;  
    }    
    int leftDepth = maxDepth(root.left);  
    int rightDepth = maxDepth(root.right);  
  
    return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;  
}  
  
  
  
/**  
 * 平衡二叉树  
 * 时间复杂度为：O(n^2)
 * @param root  
 * @return  
 */  
public boolean isBalanced(TreeNode root) {  
    if(root == null){  
        return true;  
    }   
     
    int leftDepth = maxDepth(root.left);  
    int rightDepth = maxDepth(root.right);  
    
    if(Math.abs(leftDepth - rightDepth) <= 1 &&  
            isBalanced(root.left) && isBalanced(root.right)){  
        return true;  
    }    
    return false;  
}

代码优化（字节笔试）

在时间复杂度为 O(n) 的条件下，完成平衡二叉树的判断

若要让时间复杂度为O(n)，则需要在判断的过程中，只要发现左右俩树高度相差大于 1，就直接 return -1，不再进行后续判断了

/**  
 * 获取最大深度  
 * @param root  
 * @return  
 */  
public int maxDepth(TreeNode root) {  
    if(root == null){  
        return 0;  
    }    
    int leftDepth = maxDepth(root.left);  
    if(leftDepth < 0)
    	return -1;
    int rightDepth = maxDepth(root.right);  
	if(rightDepth < 0)
		return -1;
		
    if(Math.abs(leftDepth - rightDepth) <= 1){
    	return Math.max(leftDepth, rightDepth);  
    }else {
    	return -1;
    }
}  
  
  
  
/**  
 * 平衡二叉树  
 * 时间复杂度为：O(n^2)
 * @param root  
 * @return  
 */  
public boolean isBalanced(TreeNode root) {  
    if(root == null){  
        return true;  
    }   
      
    return maxDepth(root) >= 1;  
}

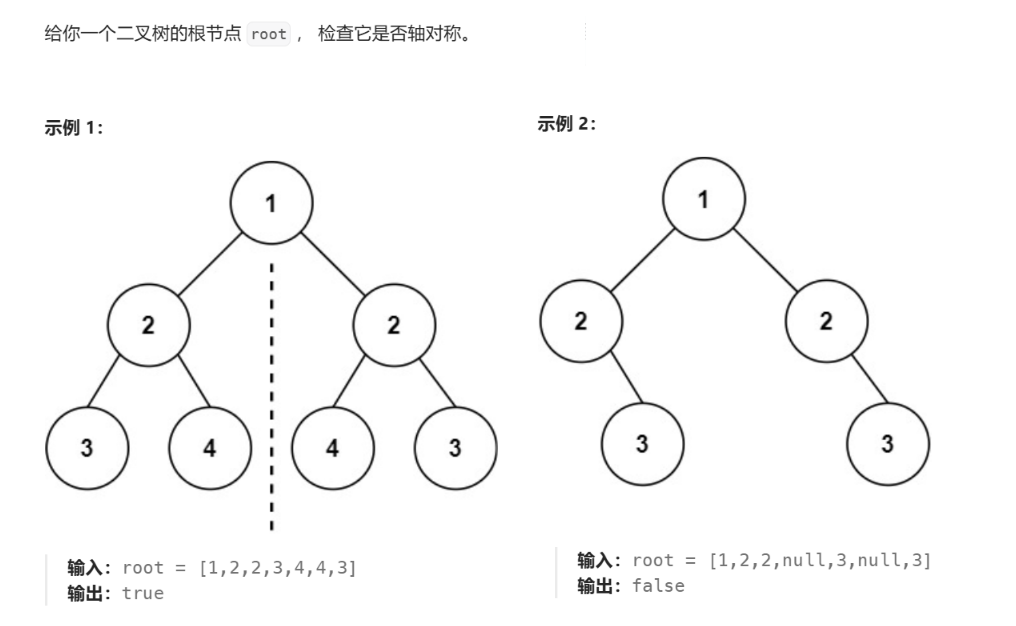
对称二叉树

101. 对称二叉树 - 力扣（LeetCode）

思路解透

需要判断 root 左树和右树是否对称

• p 的左树和 q 的右树是否对称
• p 的右树和 q 的左树是否对称

1. 结构
   1. 一个为空，一个不为空
   2. 两个都为空
   3. 两个都不为空
2. 值：建立在两个引用都不为空的情况下，判断 val

---

代码解析

public boolean isSymmetric(TreeNode root) {  
    if (root == null) return true;  
	  
    return isSymmetricChild(root.left, root.right);  
}  
  
public boolean isSymmetricChild(TreeNode leftTree, TreeNode rightTree) {  
    //1. 检查结构是否相同  
    //1.1 一个为空一个不为空  
    if (leftTree != null && rightTree == null || leftTree == null && rightTree != null) {  
        return false;  
    }    
    
    //1.2 处理两个都为空和两个都不空的情况  
    if (leftTree == null && rightTree == null) {  
        return true;  
    }    
    
    //1.3 两个都不为空，判断他们的值一不一样  
    if (leftTree.val != rightTree.val) {  
        return false;  
    }    
    
    //此时两个节点都不为空，且值一样  
    //2. 开始判断是否对称，需要满足  
    // 左子树的左 和 右子树的右对称 通同时 左子树的右 和 右子树的左对称  
    return isSymmetricChild(leftTree.left, rightTree.right) && isSymmetricChild(leftTree.right, rightTree.left);  
}