1 双亲表示法(方便查找双亲)
使用层次遍历的方法将一个树中的所有结点存储到一维数组中
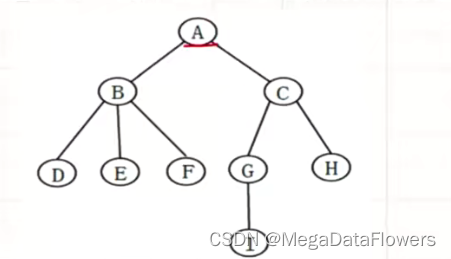
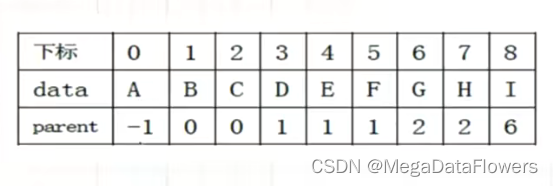
2 孩子表示法(方便查找孩子)
顺序+链式存储结构:
1 使用数组来存储所有结点
2 为每一个结点来设置一个单链表
3 单链表链接的是其所有孩子结点的下标
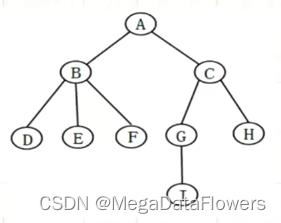
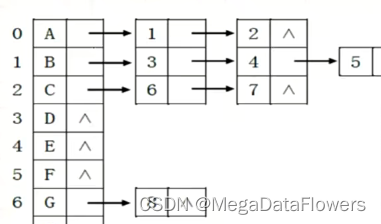
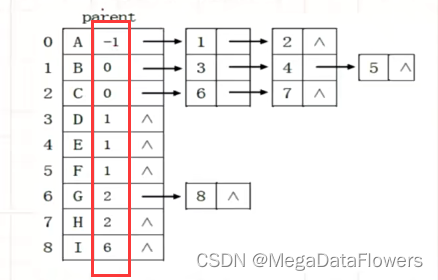
3 双亲孩子结合表示法
在孩子表示法的数组中增加一个parent区域
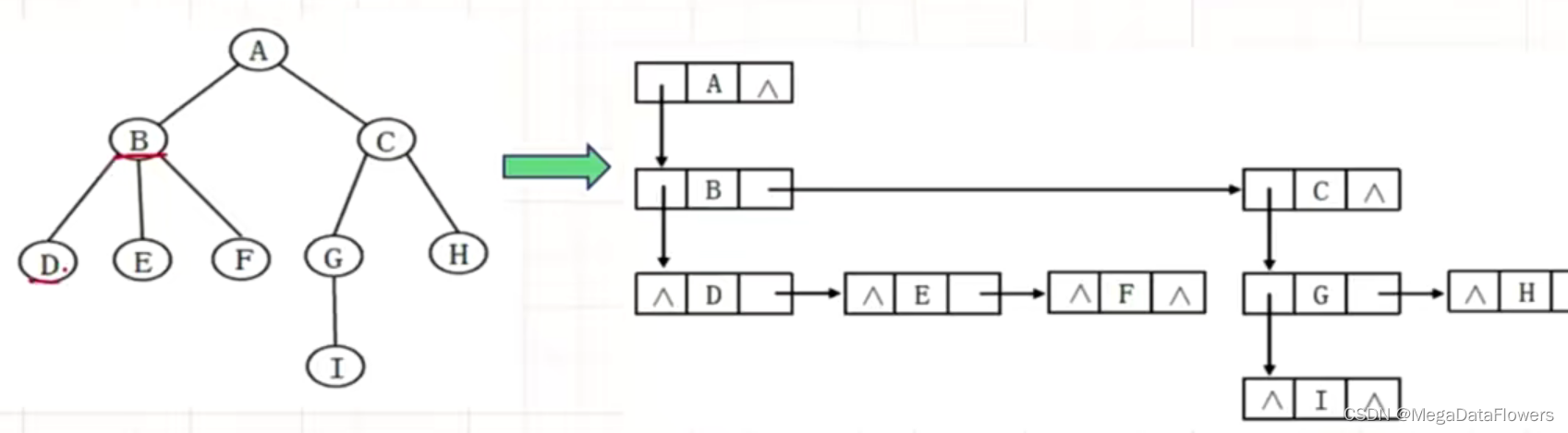
4 孩子兄弟表示法(左孩子右兄弟表示法)
**使用二叉链表作为树的存储结构**
firstChild指向结点最左侧的第一个孩子
nextSibling指向结点右侧的紧挨着的第一个兄弟

5 树到二叉树的转换
5.1 将树转化为二叉树
(将树转化为二叉树其右子树一定为空)
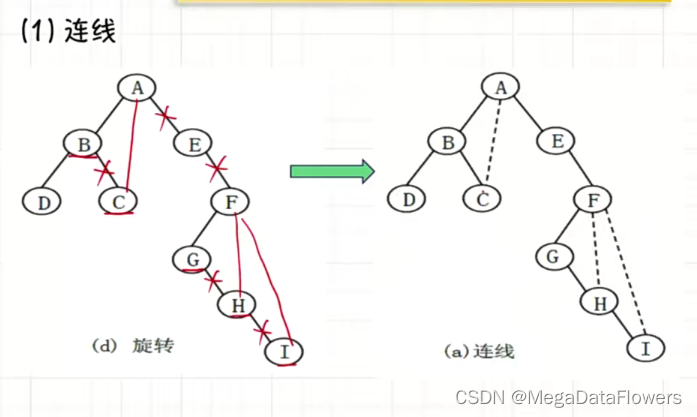
5.1.1连线
在所有的兄弟结点之间加上一条连线
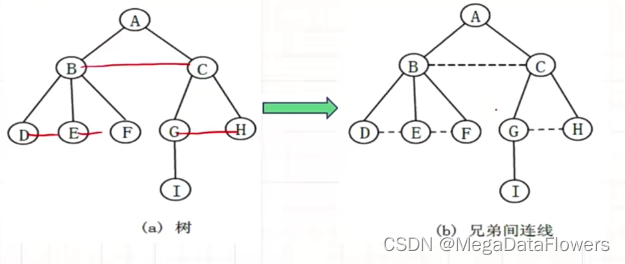
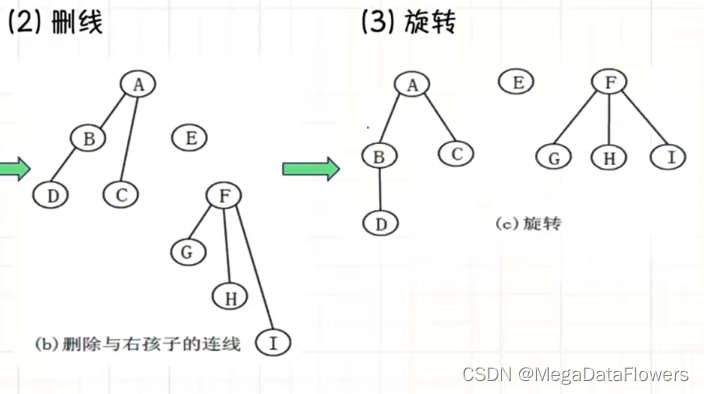
5.1.2删线
对于每个结点,除了保留与其最左孩子的连线外,删掉该结点与其它孩子之间的连线
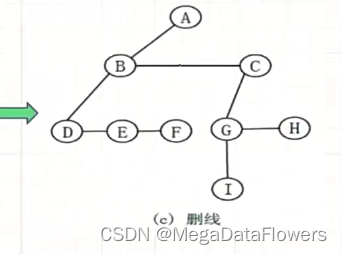
5.1.3旋转
将按照以上方法形成的二叉树,沿着顺时针方向旋转45°
就可以得到一颗二叉树
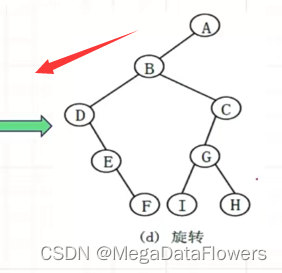
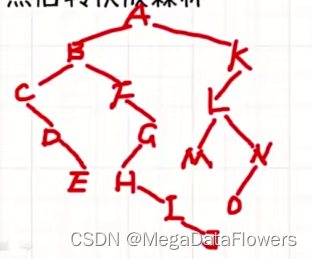
6 森林到二叉树的转换
6.1 将森林转化为二叉树
6.1.1连线
在所有的兄弟结点之间加上一条连线
(包括森林中所有树的根节点)
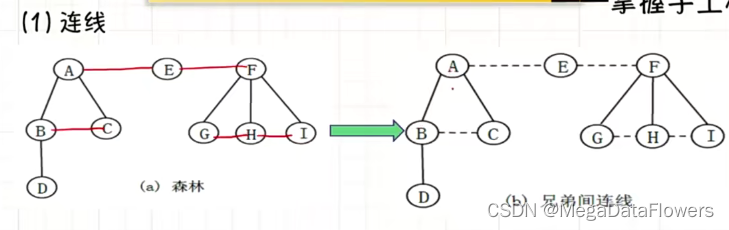
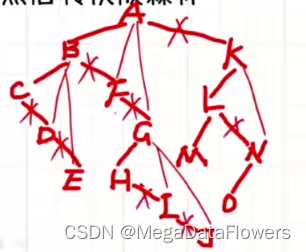
6.1.2删线
对于每个结点,除了保留与其最左孩子的连线外,删掉该结点与其它孩子之间的连线
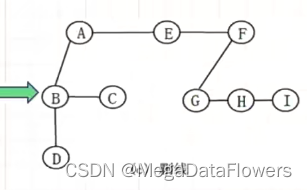
6.1.3旋转
将按照以上方法形成的二叉树,沿着顺时针方向旋转45°
就可以得到一颗二叉树
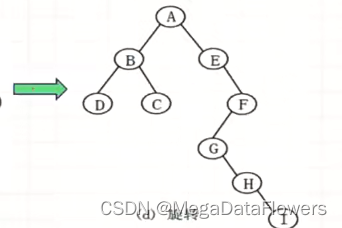

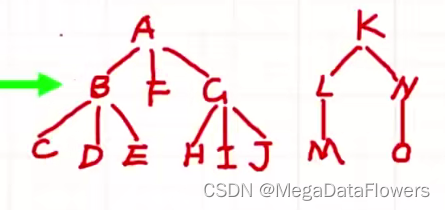
7 二叉树到森林或树的转换
是森林或树到二叉树的转换的逆过程
注意:
1 连线:如果某结点的左孩子有右子树,将该结点**与其左孩子的右子树的右链上各个结点都增加连线**
2 删线:删除二叉树中所有双亲结点与其右孩子结点的连线
8 树和森林的遍历
8.1 树和森林的深度优先遍历

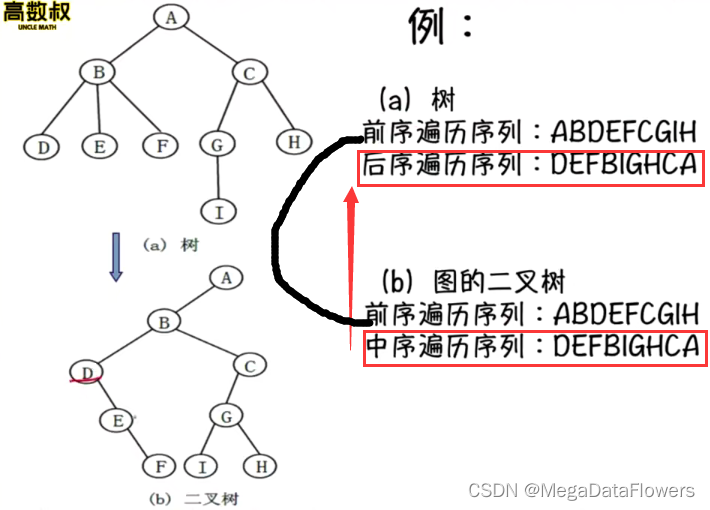
注意:
1 树的前序遍历和对应二叉树的前序遍历一样
2 树的中序(后序)遍历和对应二叉树的中序遍历一样
8.1.1 前序遍历
//实现树和森林的前序遍历
void func_qxbl(Node* t){
while(t!=NULL)
{
printf("%d\n",t->data);//访问当前结点数据
func_qxbl(t->firstChild);//前序遍历t的各个子树
t = t->nextSibling;//遍历其他的树
}
}
8.1.2 中序(也叫后序)遍历
//实现树和森林的中序(后续)遍历
void func_zhxbl(Node* t){
while(t!=NULL)
{
func_zhxbl(t->firstChild);//遍历t的各个子树
printf("%d\n",t->data);//访问当前结点数据
t = t->nextSibling;//遍历其他的树
}
}
8.1.3 总结
因为:
1 树的前序遍历和对应二叉树的前序遍历一样
2 树的中序(后序)遍历和对应二叉树的中序遍历一样
3 那么树的前序遍历代码可以写成对应二叉树的前序遍历代码
4 树的中序(后序)遍历代码可以写成对应二叉树的中序遍历代码
利用二叉树的前序遍历实现树、森林的前序遍历
void func_qxbl(Node* t){
if(t!=NULL)
{
printf("%d\n",t->data);//访问当前结点数据
func_qxbl(t->firstChild);//前序遍历第一棵子树
func_qxbl(t->nextSibling);//前序遍历其他子树
}
}
利用二叉树的中序遍历实现树、森林的中序(后序)遍历
void func_zhxbl(Node* t){
if(t!=NULL)
{
func_zhxbl(t->firstChild);//遍历第一棵子树
printf("%d\n",t->data);//访问当前结点数据
func_zhxbl(t->nextSibling);//遍历其他子树
}
}
8.2 树和森林的广度优先遍历
8.2.1 层次遍历(从上到下、从左到右)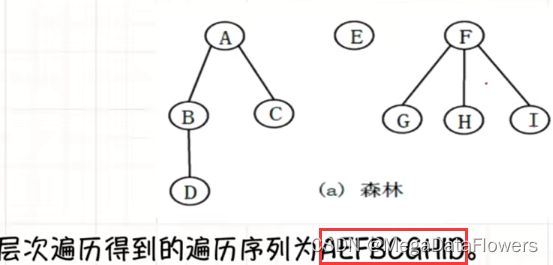
9 求树的高度
注意:
1 树和森林采用左孩子右兄弟表示法(二叉树)
使用递归前序遍历树
int height(){
if(t == NULL)
return 0;
else{
int lh = height(t->firstChild);
int rh = height(t->nextSibling);
return 1+lh>rh?lh+1:rh;
// 1+lh是t这棵树的高度
// rh是兄弟森林的高度
}
}
10 求树的结点总数
使用递归前序遍历树

int size(Node* t){
if(t == NULL)
return 0;
else
return 1+size(t->firstChild)+size(t->nextSibling);
}
11 求树的叶子结点总数
使用递归前序遍历树

int leaf(Node* t)
{
if(t == NULL)
return 0;
else{
if(t->firstChild == NULL)//当前结点是叶子结点
return 1+leaf(t->nextSibling);
else
return leaf(t->firstChild)+leaf(t->nextSibling);
}
}
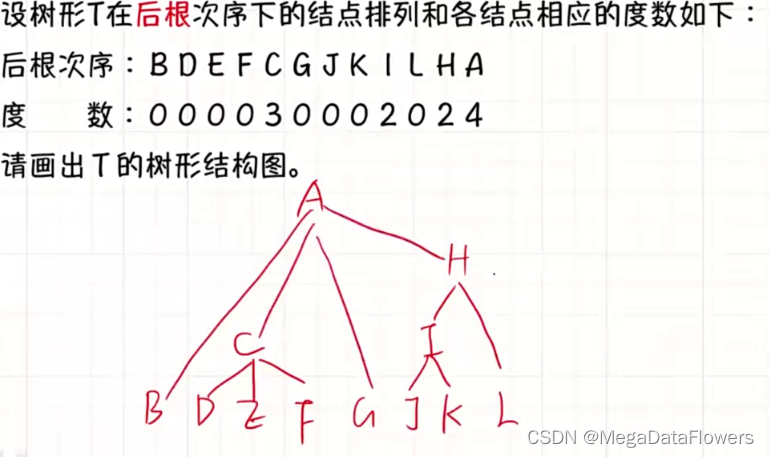
12 典型题目解析

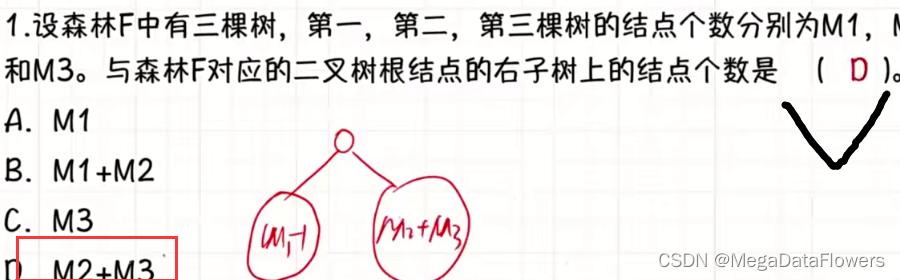
解析:
1 根据二叉树画出森林
2 判断对应关系

结论:
1 u和v可能具有的关系是:父子关系、兄弟关系

解析:
1 根据二叉树的性质:n0 = n2+1 可得
2 对于度为4的树而言:n0 = 3*n4+2*n3+1*n2+1
3 n0 = 60+20+1+1 = 82个
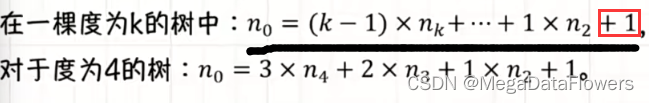
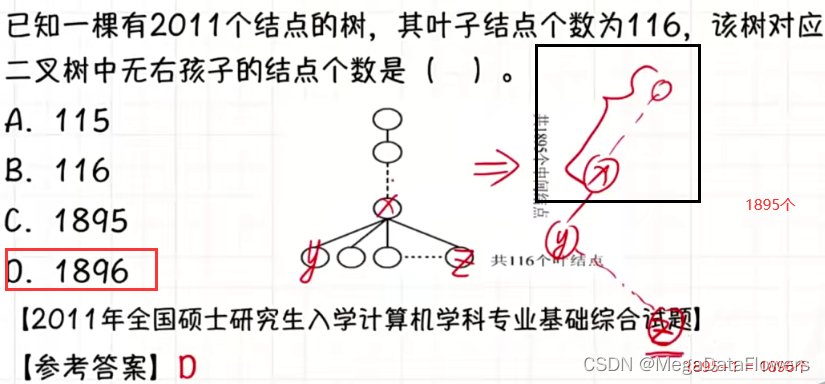

解析:
1 树和森林使用的是孩子兄弟表示法
2 如果左孩子指针为空,就不会有其他孩子了
3 其就是叶子结点
4 所以说**森林中叶子结点的个数**对应**二叉树中左孩子指针为空的结点个数**

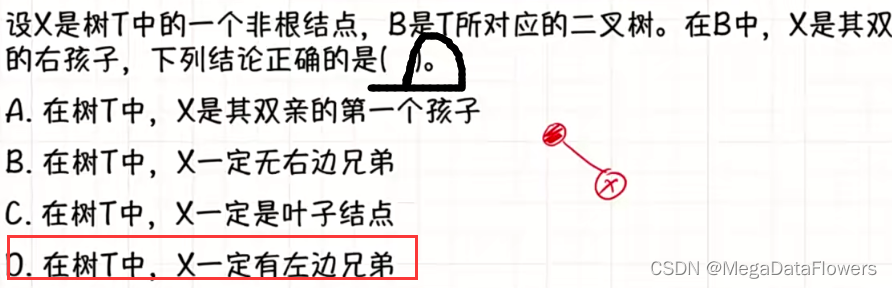
解析:
1 15条边对应16个结点
2 剩余的9个结点构成9个树
3 1+9 = 10
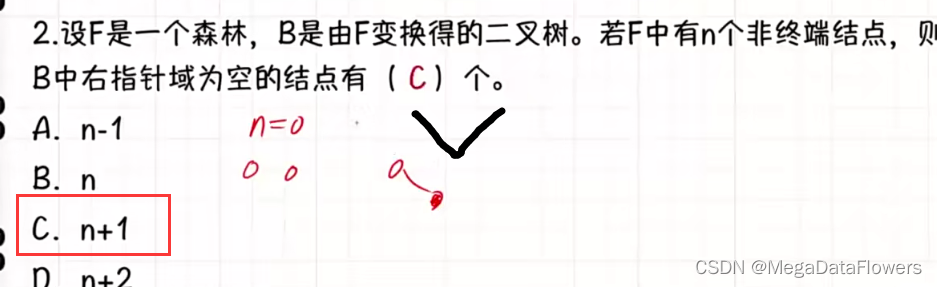



13 易错题