文章目录
- 1. 背景介绍
- 2. Loss计算公式
- 3. 使用场景
- 使用场景扩展
- 4. 代码样例
- 5. 总结
1. 背景介绍
在深度学习的世界里,损失函数犹如一把尺子,衡量着模型预测与实际结果之间的差距。均方误差损失(Mean Squared Error Loss,简称MSE Loss)作为回归问题中的常见损失函数,以其简单直观的特点,广泛应用于各种预测任务。本文将带您深入了解MSE Loss的背景、计算方法、使用场景以及如何在实际代码中应用它。
在机器学习中,损失函数是衡量模型性能的关键指标,它反映了模型预测值与真实值之间的差异。对于回归问题,我们的目标是最小化预测值与实际值之间的误差,而MSE Loss正是为此设计的。它通过计算预测值与真实值差的平方的平均值,为我们提供了一个量化误差的方法。

2. Loss计算公式
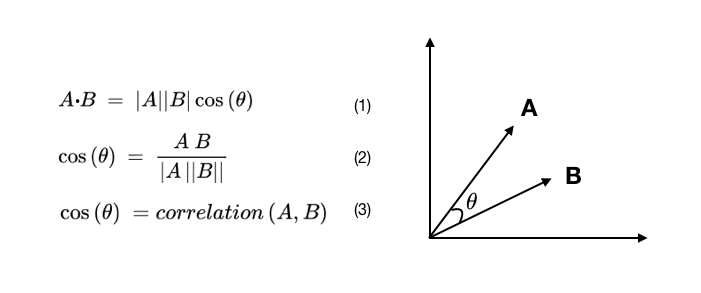
MSE Loss的计算公式如下:
MSE Loss
=
1
n
∑
i
=
1
n
(
y
i
−
y
^
i
)
2
\text{MSE Loss} = \frac{1}{n} \sum_{i=1}^{n}(y_i - \hat{y}_i)^2
MSE Loss=n1∑i=1n(yi−y^i)2
其中:
- n n n 是样本数量。
- y i y_i yi 是第 i i i个样本的真实值。
- y ^ i \hat{y}_i y^i是第 i i i个样本的预测值。
3. 使用场景
使用场景扩展
均方误差损失(MSE Loss)作为一种直观且计算效率高的损失函数,在深度学习及传统统计学领域中有着广泛的应用。以下是对MSE Loss使用场景的进一步扩展:
- 线性回归(Linear Regression)
- 在线性回归任务中,MSE Loss通过最小化预测值与实际值之间平方差的平均,引导模型学习到数据的最佳拟合线。这种应用场景非常广泛,包括但不限于房价预测、气温变化、销售额分析等,任何需要预测连续数值的场景都可能受益于MSE Loss。
- 时间序列预测(Time Series Forecasting)
- 时间序列预测是MSE Loss的另一个重要应用领域。在金融领域,它可以用来预测股票市场的趋势;在气象学中,它可以用于预测天气变化;在供应链管理中,它还可以帮助预测产品的需求波动。MSE Loss能够量化预测序列与实际观测序列之间的误差,为模型提供有效的反馈。
- 参数估计(Parameter Estimation)
- 在统计学中,MSE Loss是估计模型参数时常用的准则之一。例如,在最小二乘法中,通过最小化MSE Loss,可以找到最佳拟合参数,确保模型预测与实际观测之间的差异最小。这在构建线性模型、多项式回归或其他形式的参数化模型时尤为重要。
- 机器学习模型的正则化(Regularization in Machine Learning)
- MSE Loss不仅用于直接的预测误差度量,还可以作为正则化项的一部分,帮助控制模型的复杂度,防止过拟合。例如,在岭回归(Ridge Regression)和套索回归(Lasso Regression)中,MSE Loss与正则化项结合使用,以达到模型优化的目的。
- 计算机视觉(Computer Vision)
- 在计算机视觉领域,MSE Loss可以用于像素级的预测任务,如图像重建、去噪、图像超分辨率等。尽管在这些任务中MSE Loss可能不是首选损失函数,但在某些情况下,它仍然提供了一种简单有效的误差度量方式。
- 强化学习(Reinforcement Learning)
- 在强化学习中,MSE Loss有时被用作价值函数或策略的损失函数,特别是在连续动作空间的设置中。通过最小化MSE Loss,可以帮助智能体学习如何根据环境状态做出决策。
- 信号处理(Signal Processing)
- 在信号处理领域,MSE Loss用于评估信号重建的质量,如在滤波、去噪和信号估计等任务中。它提供了一种量化信号失真程度的方法。
- 推荐系统(Recommender Systems)
- 在推荐系统中,MSE Loss可以用于评估预测评分与实际评分之间的差异,帮助模型学习更准确的用户偏好。
MSE Loss因其简单性、直观性和易于优化的特性,在多个领域内都有着不可或缺的作用。然而,它对异常值敏感,这可能在某些情况下导致问题。因此,在使用MSE Loss时,需要根据具体问题和数据特性综合考虑,有时还需要与其他损失函数结合使用,以达到更好的效果。
4. 代码样例
以下是使用Python和PyTorch库实现MSE Loss的示例代码:
import torch
import torch.nn as nn
# 假设我们有一些预测值和真实值
predictions = torch.tensor([2.5, 3.0, 4.0], requires_grad=True)
targets = torch.tensor([3.0, 3.5, 2.0])
# 定义MSE Loss
criterion = nn.MSELoss()
# 计算损失
loss = criterion(predictions, targets)
# 打印损失值
print("Loss:", loss.item())
# 反向传播,计算梯度
loss.backward()
# 打印梯度
print("Gradients:", predictions.grad)
5. 总结
均方误差损失(MSE Loss)以其直观的计算方式和广泛的适用性,在深度学习回归任务中占据了重要地位。然而,MSE Loss也有一些局限性,比如对异常值敏感,这可能在某些情况下导致模型性能受影响。因此,在实际应用中,我们可能需要根据具体问题选择或设计更合适的损失函数。无论如何,MSE Loss都是深度学习从业者必须掌握的基本工具之一。