目录
Are Consultants Worth It?
Crash Course in Graphical Models
Chains
Are Consultants Worth It?
为了展示有向无环图(DAG)的力量,让我们考虑一个更有趣但处理因素并未随机化的情况。假设你是某公司的经理,正在考虑是否聘请顶级咨询顾问。你知道聘请他们代价高昂,但同时你了解他们拥有在业内顶尖公司工作的专业知识。使问题复杂化的是,你不确定是顶级咨询顾问提升了公司的业务表现,还是只有非常盈利的公司才能负担得起这些顾问,因此他们的存在与强劲的业务表现相关联。如果有人能随机安排咨询顾问的参与,那解答这个问题就简单多了。但当然,你没有这样的便利,所以你必须另寻他法。正如你现在可能已经意识到的,这是一个将因果关系从关联中剥离出来的问题。为了理解这一点,你可以将你对因果机制的信念编码在一个图中: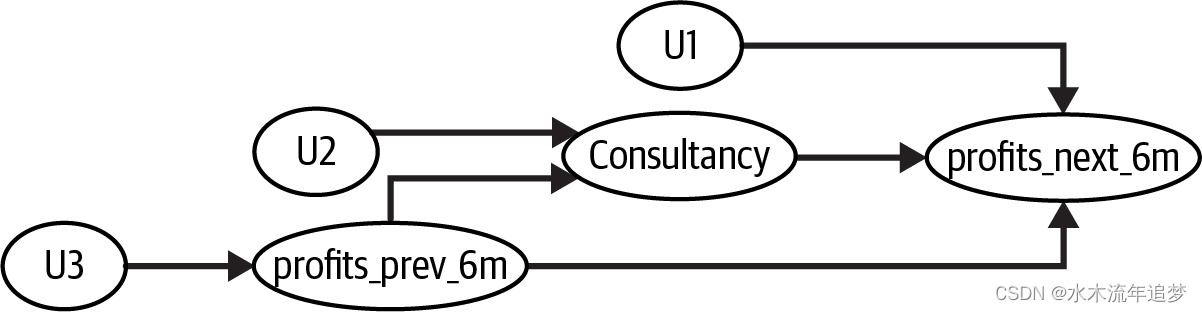
注意到我在这些变量中都加入了U节点,以表示还有其他我们无法衡量的因素在起作用。因为图通常代表随机变量,可以预期所有变量都会受到某种随机成分的影响,这就是U所代表的意义。然而,它们对接下来我要讲述的因果故事不会增加任何内容,所以我可能干脆省略它们:

在这里,我表明公司的过往表现决定了公司是否会聘请顶级咨询顾问。如果公司业绩良好,它可以负担得起昂贵的服务费用;如果公司业绩不佳,则无法承担。因此,过往表现(此处以过往利润衡量)决定了公司聘请咨询顾问的可能性。需要记住的是,这种关系不一定具有确定性。我只是说,业绩良好的公司更有可能聘请顶级咨询顾问。
不仅如此,过去6个月业绩良好的公司很可能在未来6个月也会表现出色。当然,这种情况并不总是发生,但平均而言确实如此,这就是为什么图中还有一条从过往表现到未来表现的边。最后,我还加入了一条从咨询顾问到公司未来表现的边。你的目标是了解这条连接的强度。这是你关心的因果关系。咨询顾问真的能提升公司业绩吗?
回答这个问题并不直接,因为咨询顾问与未来表现之间的关联有两个来源。一个是因果性的,另一个则不是。为了理解并区分这两种关联,首先你需要快速了解一下关联在因果图中的流动方式。
Crash Course in Graphical Models
学校会提供整个学期的课程来教授图形模型。毫无疑问,如果你想深入研究图形模型,这对你的因果推断理解将会大有裨益。但是最重要的是你需要理解图形模型所蕴含的独立性和条件独立性假设。如你将看到的,关联在图形模型中的流动就如同水流过溪流一般。根据你如何处理图中的变量,你可以阻止这种流动或使其得以实现。为了理解这一点,让我们考察一些常见的图形结构和例子。它们将非常直观,但却是理解图形模型中关联、独立性和条件独立性流动的所有必要基石。
Chains
首先,看看这个非常简单的图。它被称为链式结构。在这里,T导致M的发生,而M又导致Y的发生。有时,中间节点可以被称为中介变量,因为它介导了T和Y之间的关系:
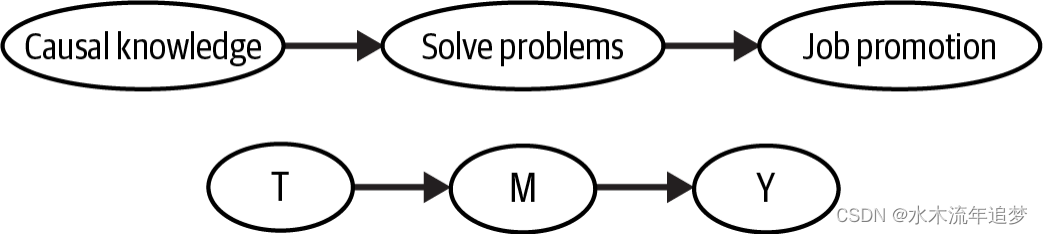
在这个第一个图中,尽管因果关系只沿着箭头的方向流动,但关联却可以双向流动。为了给出一个更具体的例子,假设了解因果推断能提高你的解决问题技能,而解决问题的能力增强会增加你获得晋升的机会。因此,因果知识导致你的解决问题技能提升,反过来又导致你得到职位晋升。可以说,职位晋升依赖于因果知识。因果专长越强,你得到晋升的机会越大。同时,晋升机会越大,你拥有因果知识的可能性也越高。否则,很难获得晋升。换句话说,职位晋升与因果推断专长相关联,就像因果推断专长与职位晋升相关联一样,尽管只有一个方向是因果的。
当两个变量相互关联时,可以说它们是相互依赖的或非独立的:
现在,让我们固定中间变量。在我们的例子中,你可以通过只看具有相同M(解决问题技能)的人来做到这一点。正式地说,你可以说你是在M条件下进行的。在这种情况下,依赖关系被阻断。因此,给定M时,T和Y是独立的。你可以用数学语言这样表示:
为了表示我们正在对一个节点进行条件化,我会将其涂黑: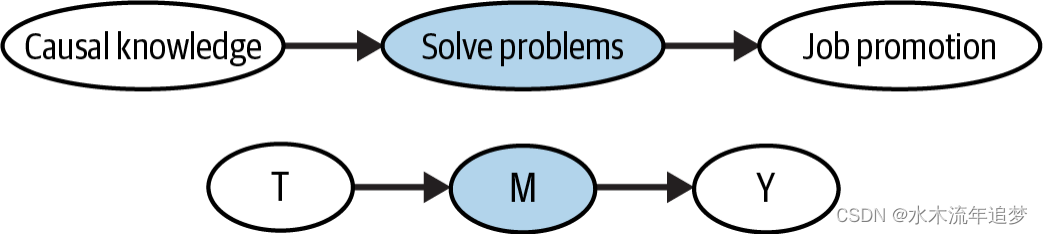
在我们的例子中,考虑对人们的解决问题技能进行条件化。如果你看一群具有相同解决问题技能的人,知道他们中谁擅长因果推断并不能提供更多关于他们获得职位晋升机会的信息。用数学语言表示就是:
反之亦然;一旦我知道你解决问题的能力有多强,了解你的职位晋升状态并不能给我更多关于你了解因果推断的可能性的信息。
一般来说,如果你有一个像前面图中那样的链式结构,从T到Y的路径中流动的关联会在你对中间变量M进行条件化时被阻断。或者可以表示为: 但
![[数据结构] AVL树 模拟实现AVL树](https://i-blog.csdnimg.cn/direct/2d658cb51c264b8fb5571c3fe5950691.png)