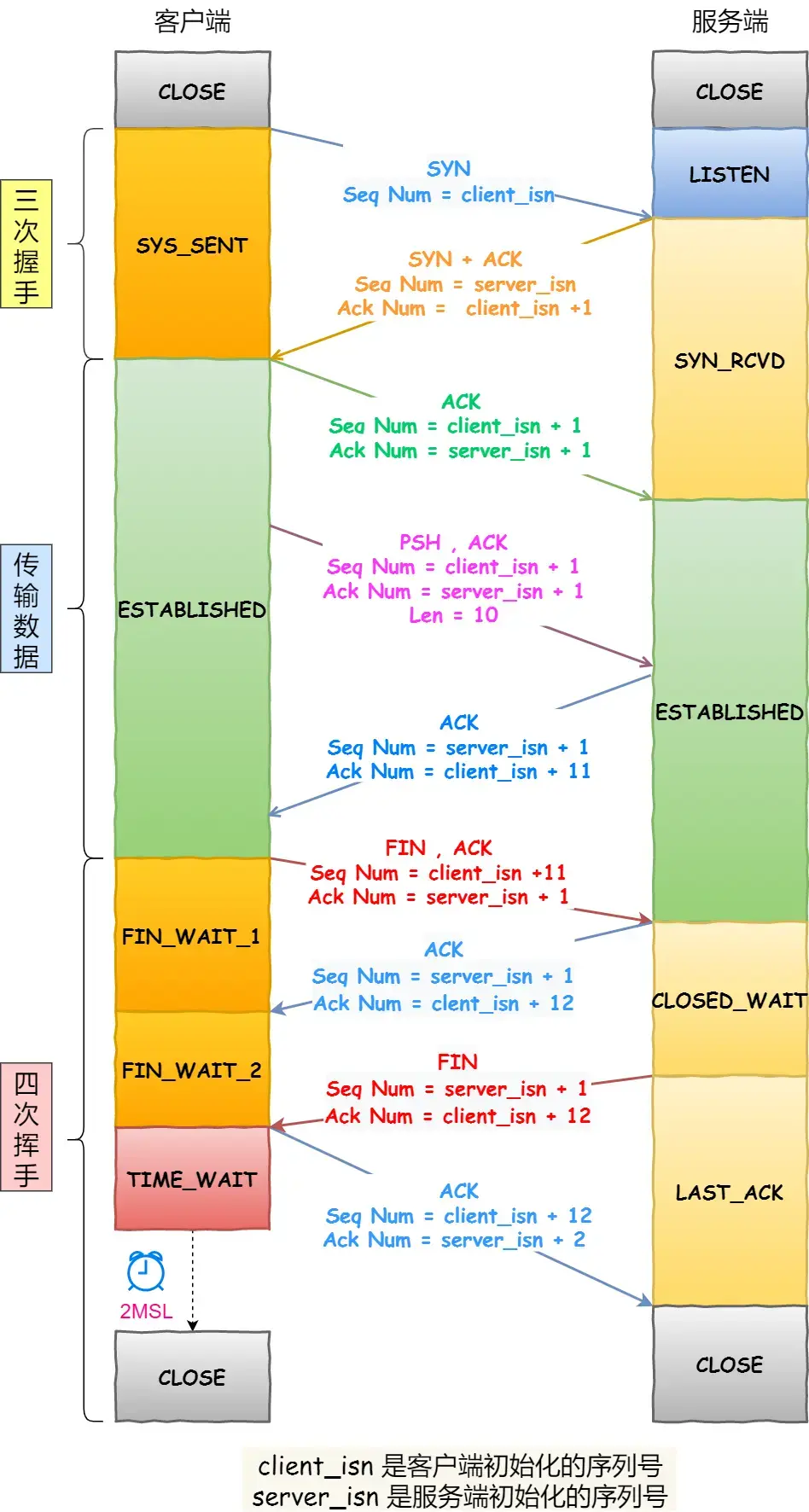
二叉树的题目根据不同的题目特点需要用不同的递归算法或者层序遍历实现。
递归三要素
- 根据题目要求:确定递归函数的参数和返回值;
- 根据题目要求:确定递归函数的终止返回条件;
- 根据题目要求:确定单层的递归逻辑。
层序遍历

#include<iostream>
#include<vector>
#include<queue>
using namespace std;
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> res;
vector<int> path;
queue<TreeNode *> q;
if(root)
q.push(root);
while(!q.empty())
{
int sz=q.size();
path.clear();
for(int i=0;i<sz;i++)
{
auto top=q.front();
q.pop();
path.push_back(top->val);
if(top->left)
q.push(top->left);
if(top->right)
q.push(top->right);
}
res.push_back(path);
}
return res;
}
int main(){
TreeNode* node1=new TreeNode(3);
TreeNode* node2=new TreeNode(9);
TreeNode* node3=new TreeNode(20);
TreeNode* node4=new TreeNode(15);
TreeNode* node5=new TreeNode(7);
node1->left=node2;
node1->right=node3;
node3->left=node4;
node3->right=node5;
auto ans=levelOrder(node1);
for(int i=0;i<ans.size();i++)
{
for(int j=0;j<ans[i].size();j++)
{
if(j==ans[i].size()-1)
cout<<ans[i][j];
else
cout<<ans[i][j]<<",";
}
cout<<endl;
}
return 0;
}


二叉树的层序遍历II
给你二叉树的根节点 root ,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
只需将层序遍历的结果reverse即可。
二叉树的左视图
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从左侧所能看到的节点值。

vector<int> leftWideView(TreeNode* root)
{
vector<int> res;
queue<TreeNode*> q;
if(root)
q.push(root);
while(!q.empty()){
int sz=q.size();
for(int i=0;i<sz;i++)
{
auto top=q.front();
q.pop();
if(i==0)
{
res.push_back(top->val);
}
if(top->left) q.push(top->left);
if(top->right) q.push(top->right);
}
}
return res;
}
int main(){
TreeNode* node1=new TreeNode(3);
TreeNode* node2=new TreeNode(9);
TreeNode* node3=new TreeNode(20);
TreeNode* node4=new TreeNode(15);
TreeNode* node5=new TreeNode(7);
node1->left=node2;
node1->right=node3;
node3->left=node4;
node3->right=node5;
auto res=leftWideView(node1);
for(int i=0;i<res.size();i++)
{
if(i==res.size()-1)
{
cout<<res[i];
}
else{
cout<<res[i]<<',';
}
}
cout<<endl;
return 0;
}

二叉树的右视图
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。

class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
queue<TreeNode*> q;
if(root)
{
q.push(root);
}
vector<int> res;
while(!q.empty())
{
int sz=q.size();
for(int i=0;i<sz;i++)
{
auto top=q.front();
q.pop();
if(i==sz-1)
res.push_back(top->val);
if(top->left) q.push(top->left);
if(top->right) q.push(top->right);
}
}
return res;
}
};二叉树的层平均值
注意sum要是double类型。
给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。
class Solution {
public:
vector<double> averageOfLevels(TreeNode* root) {
vector<double> res;
queue<TreeNode*> q;
if(root)
q.push(root);
while(!q.empty())
{
int sz=q.size();
double sum=0;
for(int i=0;i<sz;i++)
{
auto top=q.front();
q.pop();
sum+=top->val;
if(top->left) q.push(top->left);
if(top->right) q.push(top->right);
}
res.push_back(sum/sz);
}
return res;
}
};在每个🌲中找最大值
class Solution {
public:
vector<int> largestValues(TreeNode* root) {
vector<int> res;
queue<TreeNode*> q;
if (root)
q.push(root);
while (!q.empty()) {
int sz = q.size();
int tmp=INT_MIN;
for (int i = 0; i < sz; i++) {
auto top = q.front();
q.pop();
tmp=max(tmp,top->val);
if (top->left)
q.push(top->left);
if (top->right)
q.push(top->right);
}
res.push_back(tmp);
}
return res;
}
};二叉树的最大深度
- 二叉树深度:从根节点到该节点的最短路径长度,越往下越大
- 二叉树高度: 从该结点到叶子节点的最短路径长度,越往下越小
- 根节点的高度就是二叉树的最大深度
class Solution {
public:
int maxDepth(TreeNode* root) {
int res = 0;
queue<TreeNode*> q;
if (root)
q.push(root);
while (!q.empty()) {
int sz = q.size();
for (int i = 0; i < sz; i++) {
auto top = q.front();
q.pop();
if(top->left) q.push(top->left);
if(top->right) q.push(top->right);
}
res++;
}
return res;
}
};二叉树的最小深度
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
class Solution {
public:
int minDepth(TreeNode* root) {
int res=1;
queue<TreeNode*> q;
if(!root) return 0;
if(root) q.push(root);
while(!q.empty())
{
int sz=q.size();
for(int i=0;i<sz;i++)
{
auto top=q.front();
q.pop();
if(!top->left&&!top->right)
{
return res;
}
if(top->left) q.push(top->left);
if(top->right) q.push(top->right);
}
res++;
}
return res;
}
};完全二叉树节点的个数
class Solution {
public:
int countNodes(TreeNode* root) {
int res=0;
queue<TreeNode*> q;
if(!root) return 0;
if(root) q.push(root);
while(!q.empty())
{
int sz=q.size();
for(int i=0;i<sz;i++)
{
auto top=q.front();
q.pop();
if(top->left) q.push(top->left);
if(top->right) q.push(top->right);
}
res+=sz;
}
return res;
}
};翻转二叉树
翻转二叉树其实就是将根节点 的左右子树互换,因此前序和后序遍历都可以。
but层序遍历依然可以。
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
queue<TreeNode*> q;
if(root) q.push(root);
while(!q.empty())
{
int sz=q.size();
for(int i=0;i<sz;i++)
{
auto front=q.front();
q.pop();
swap(front->left,front->right);
if(front->left) q.push(front->left);
if(front->right) q.push(front->right);
}
}
return root;
}
};找树左下角的值
该二叉树的 最底层 最左边 节点的值。即最后一层的第一个节点。

class Solution {
public:
int findBottomLeftValue(TreeNode* root) {
int res=0;
queue<TreeNode*> q;
if(root) q.push(root);
while(!q.empty())
{
int sz=q.size();
for(int i=0;i<sz;i++)
{
auto front=q.front();
q.pop();
// 无需判断,只要依次记录每一层的第一个。最后一个就是最后一层的第一个。
if(i==0) res=front->val;
if(front->left) q.push(front->left);
if(front->right) q.push(front->right);
}
}
return res;
}
};
N叉树的层序遍历
递归-迭代
平衡二叉树
如何判断以当前传入节点为根节点的二叉树是否是平衡二叉树呢?其左子树高度和其右子树高度的差值<2。所以是后续遍历,且当以遍历的子树为-1时,说明整棵树就已经不剩平很二叉树了。
class Solution {
public:
int getHeight(TreeNode* root){
if(!root) return 0;
int leftH=getHeight(root->left);
if(leftH==-1) return -1;
int rightH=getHeight(root->right);
if(rightH==-1) return -1;
if(abs(leftH-rightH)>1)
return -1;
else
return max(leftH,rightH)+1;
}
bool isBalanced(TreeNode* root) {
return getHeight(root)==-1?false:true;
}
};二叉树的所有路径
返回所有从根节点到叶子节点的路径。
题目要求从根节点到叶子的路径,所以需要前序遍历,这样才方便让父节点指向孩子节点,找到对应的路径。
class Solution {
public:
vector<string> res;
vector<int> path;
void backtrack(TreeNode* root)
{
path.push_back(root->val);// 先序遍历
if(!root->left&&!root->right)//到叶子节点时,记录每一个结果
{
string sPath;
for(int i=0;i<path.size();i++)
{
if(i!=path.size()-1)
{
sPath+=to_string(path[i]);
sPath+="->";
}
else
{
sPath+=to_string(path[path.size()-1]);
}
}
res.push_back(sPath);
return;
}
if(root->left)
{
backtrack(root->left);
path.pop_back();
}
if(root->right)
{
backtrack(root->right);
path.pop_back();
}
}
vector<string> binaryTreePaths(TreeNode* root) {
backtrack(root);
return res;
}
};左叶子之和
左叶子的定义:节点A的左孩子不为空,且左孩子的左右孩子都为空(说明是叶子节点),那么A节点的左孩子为左叶子节点 。

递归的遍历顺序为后序遍历(左右中),是因为要通过递归函数的返回值来累加求取左叶子数值之和。
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
if(!root) return 0;
if(!root&&!root) return 0;// 不符合左叶子定义
int leftV=sumOfLeftLeaves(root->left);
if(root->left&&!root->left->left&&!root->left->right)
leftV=root->left->val;
int rightV=sumOfLeftLeaves(root->right);
return leftV+rightV;
}
};