链式栈
链式存储的栈
实现方式:可以使用单向链表完成
对单向链表进行头插(入栈)、头删(出栈),此时链表的头部就是链栈的栈顶,链表的尾部,就是链栈的栈底
队列
概念
队列:操作受限的线性表,插入和删除只能在异端操作
队列的特点:先进先出(FIFO),后进后出(LILO
队头:可以进行删除的一段
队尾:可以进行插入的一段
队列的种类:顺序队列,链式队列
顺序队列
顺序存储的队列(保证存储的数据逻辑上相邻,物理内存上也相连,还要保证符合队列的特点)
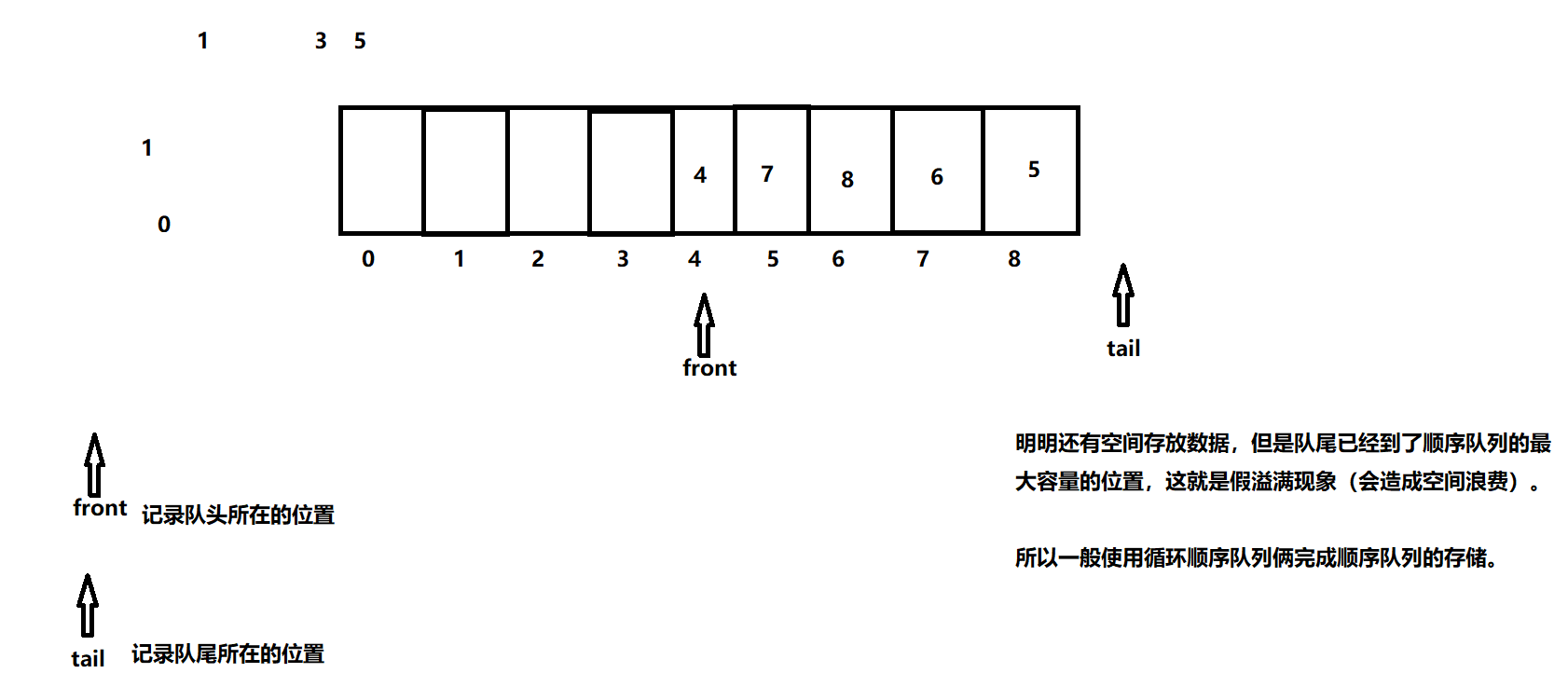
顺序队列的组成
需要一片连续的空间存放数据(数组,堆区的一片连续的空间)
需要一个变量记录队头的位置
需要一个变量记录队尾的位置(最后一个元素的下一个元素的位置)
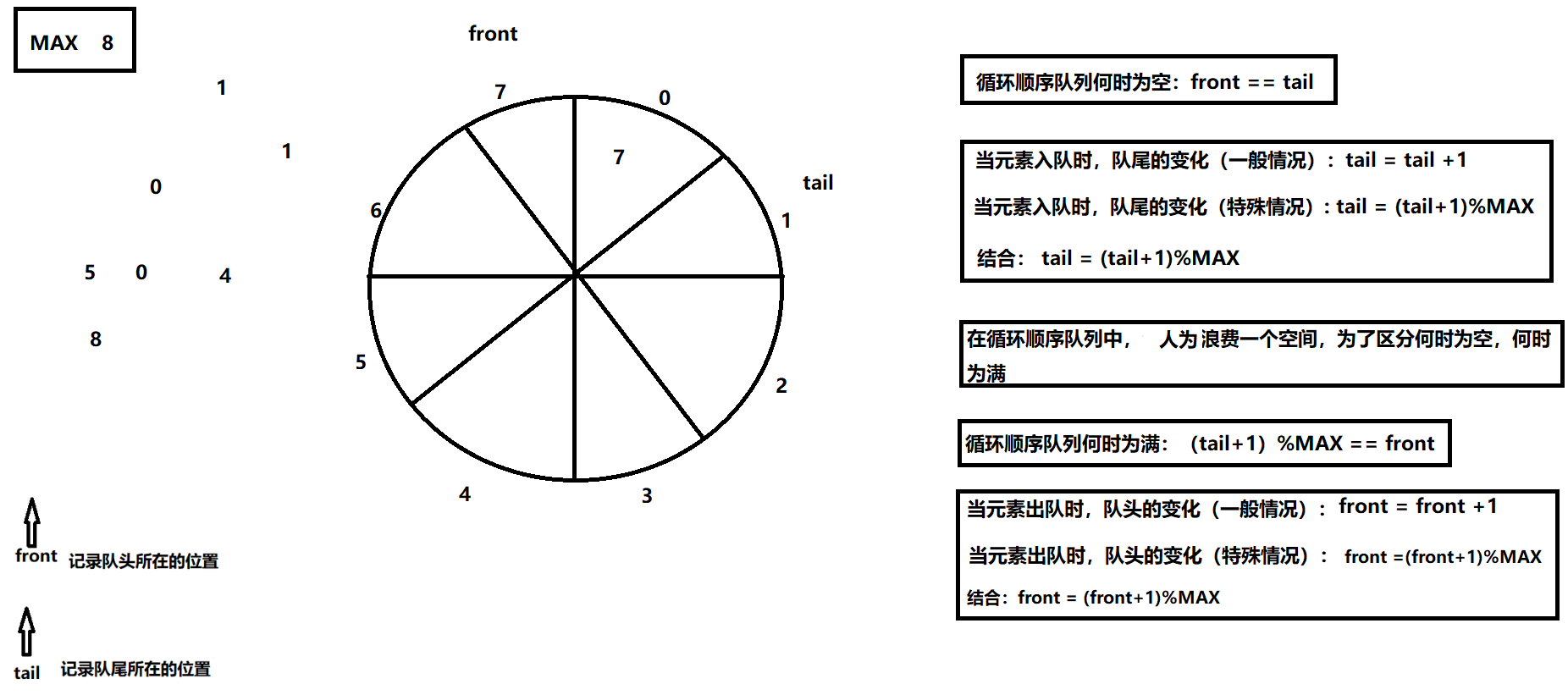
假溢满现象
还有位置存放数据,但是队尾已经到了顺序队列的最大容量的位置
所以一般采用循环队列来完成顺序队列的存储
循环顺序队列
循环顺序队列的组成
需要一片连续的空间存放数据(数组,堆区的一片连续的空间)
需要一个变量记录队头的位置
需要一个变量记录队尾的位置(最后一个元素的下一个元素的位置)
循环顺序队列的结构体原型
//宏定义 循环顺序队列的最大容量
#define MAX 30
//类型重定义,表示要存储数据的类型
typedef int DataType;
//定义循环顺序队列的结构体类型
typedef struct sequence
{
DataType data[MAX]; //用数组存放数据,实现逻辑相连,物理内存也相连
int front; //记录队头所在的位置
int tail; //记录队尾所在的位置
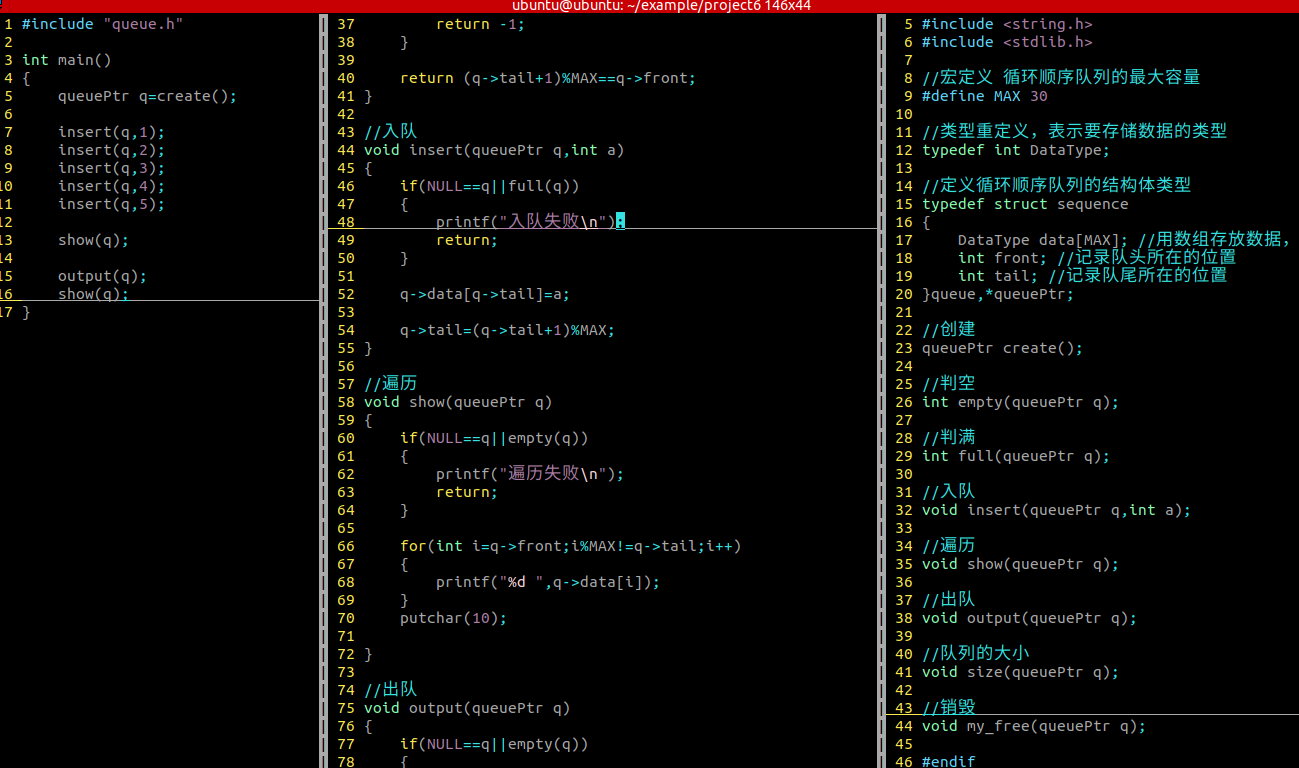
}queue,*queuePtr;循环顺序队列的相关操作(功能函数的封装)
创建
函数返回值:顺序栈的指针
参数列表:无
判断申请空间是否合法
判空
参数列表:顺序队列
判断申请空间是否合法
判满
参数列表:顺序队列
判断申请空间是否合法

入队
参数列表:顺序队列,入队的值
判断申请空间是否合法
需要判满
遍历
参数列表:顺序队列
判断申请空间是否合法
需要判空
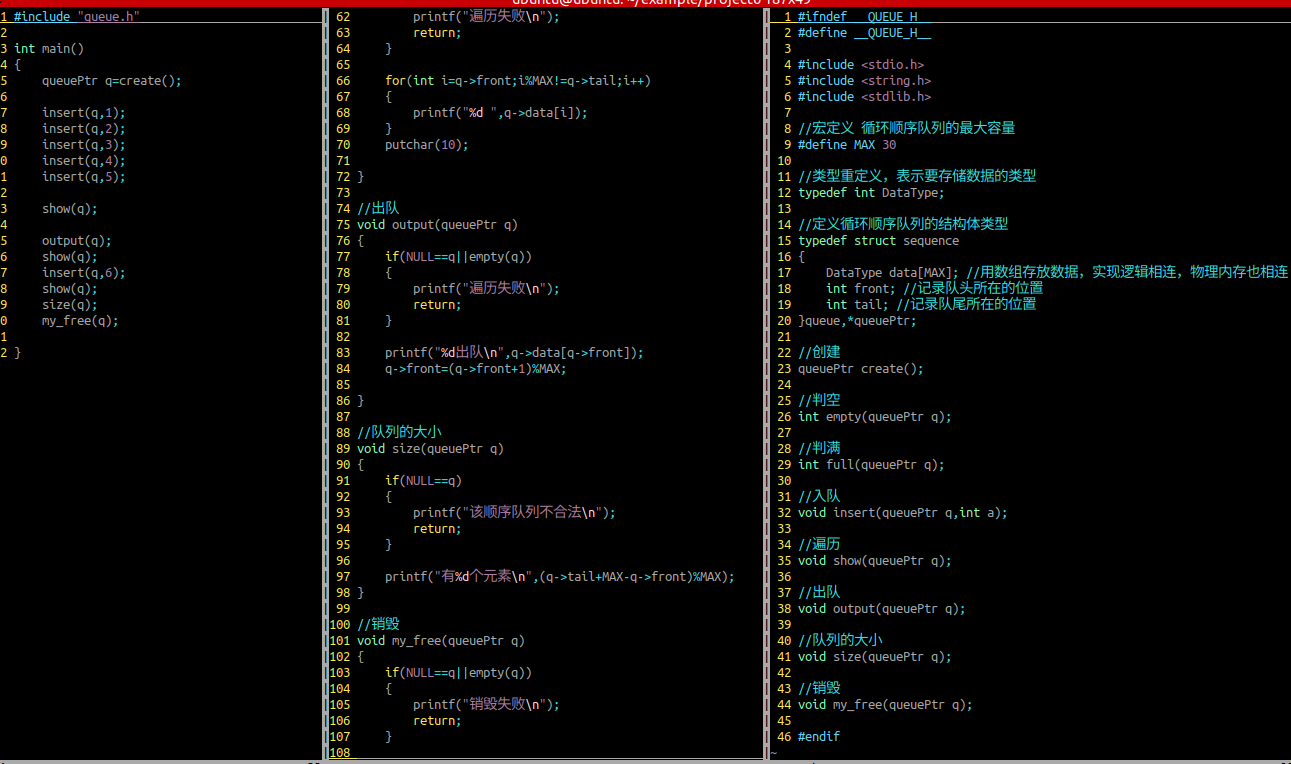
出队
参数列表:顺序队列
判断申请空间是否合法
需要判空
顺序队列的大小
参数列表:顺序队列
判断申请空间是否合法
销毁
参数列表:顺序队列
判断申请空间是否合法
链式队列
链式存储的队列(保证存储的数据逻辑上相连,物理内存上随机存储,保证满足队列的特点)
链式队列的组成
需要一片连续的空间存放数据(数组,堆区的一片连续的空间)
需要一个变量记录队头的位置
需要一个变量记录队尾的位置(最后一个元素的下一个元素的位置)
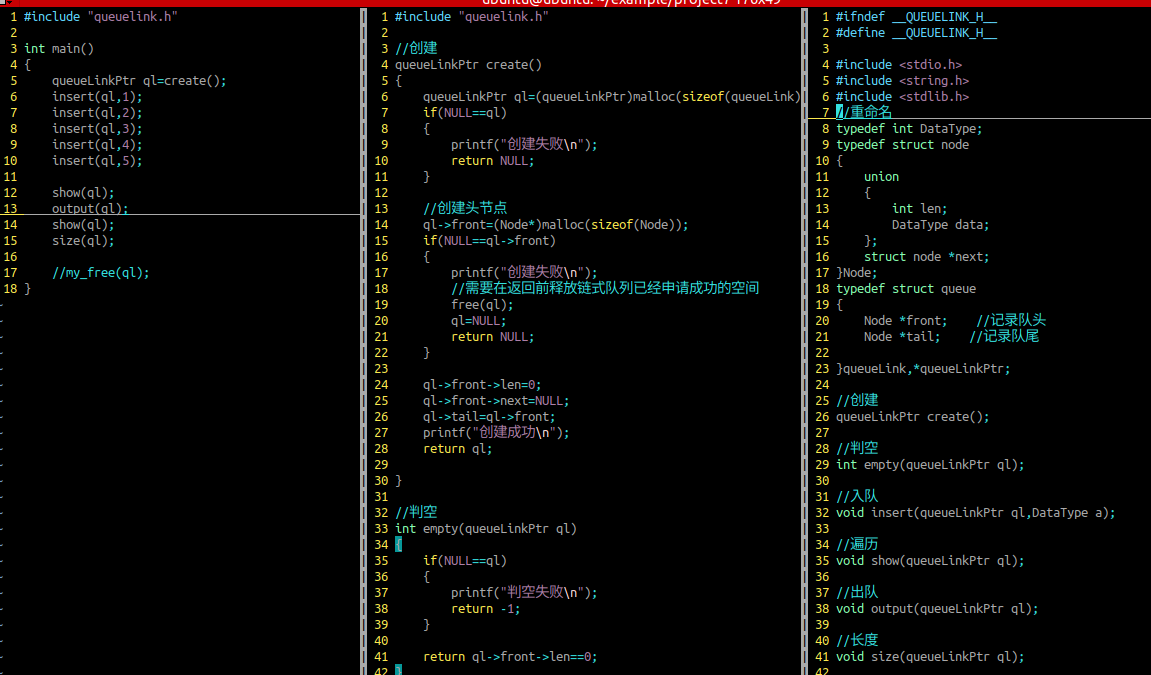
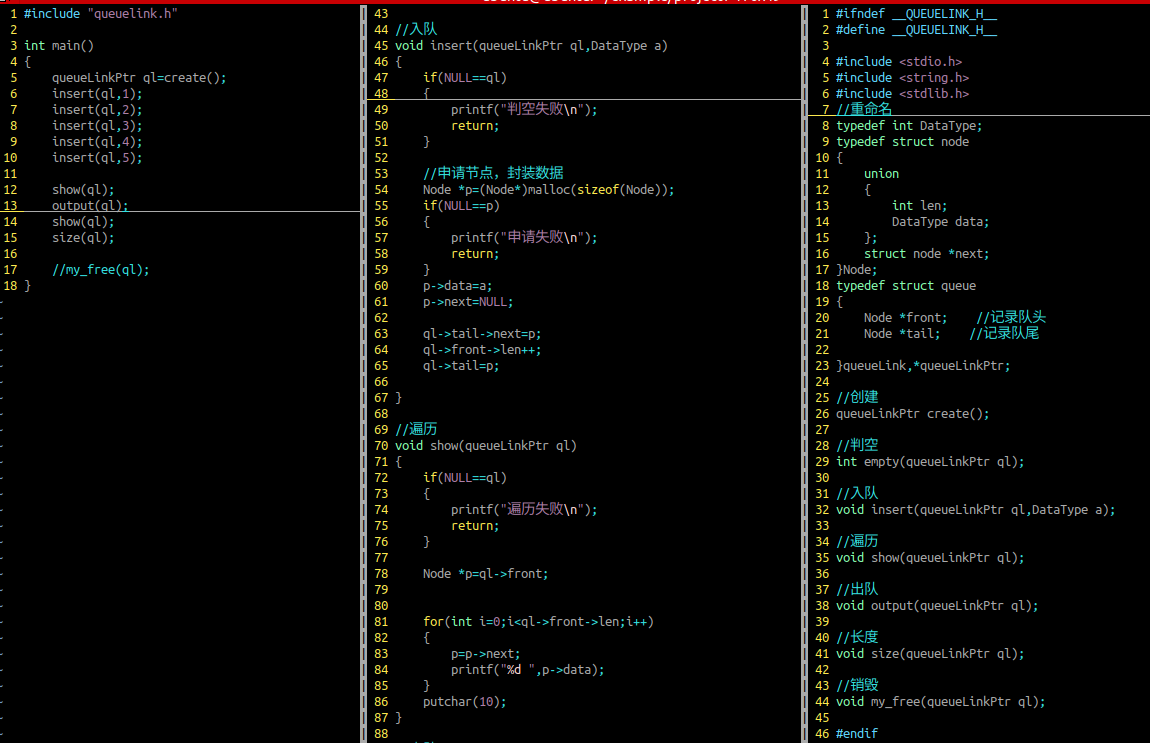
链式队列的节点的结构体原型
//重命名
typedef int DataType;
typedef struct node
{
union
{
int len;
DataType data;
};
struct node *next;
}Node;
typedef struct queue
{
Node *front; //记录队头
Node *tail; //记录队尾
}queueLink,*queueLinkPtr;链式队列的相关操作(功能函数的封装)
创建
参数列表:无
判断申请空间是否合法
判空
参数列表:顺序队列
判断申请空间是否合法
入队(尾插)
参数列表:顺序队列,入队的数据
判断申请空间是否合法
遍历
参数列表:顺序队列
判断申请空间是否合法
需要判空
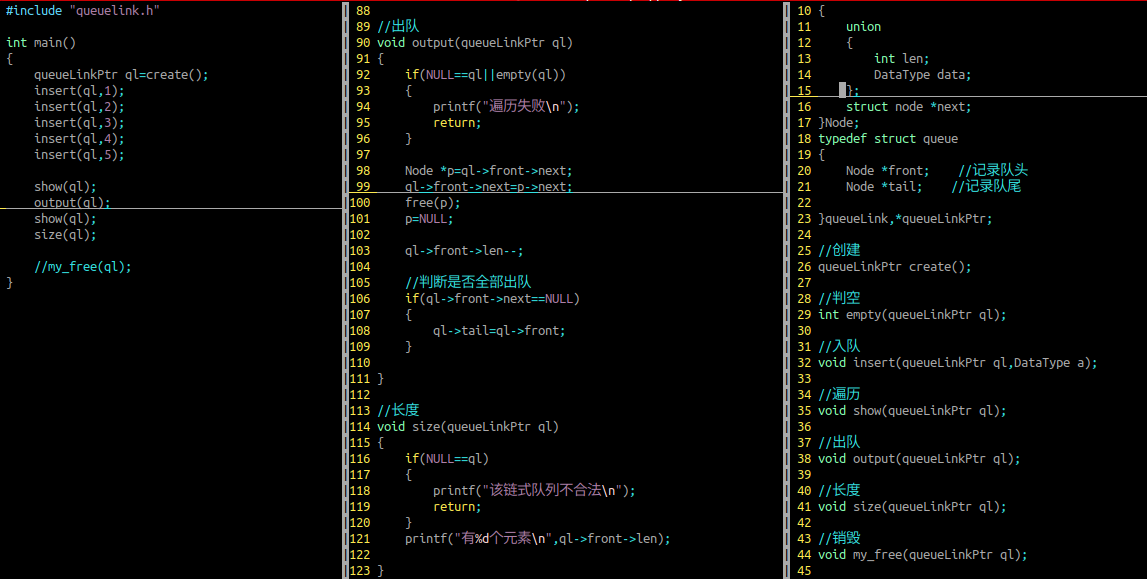
出队(头删)
参数列表:顺序队列
判断申请空间是否合法
需要判空
队列的大小
参数列表:顺序队列
判断申请空间是否合法
需要判空
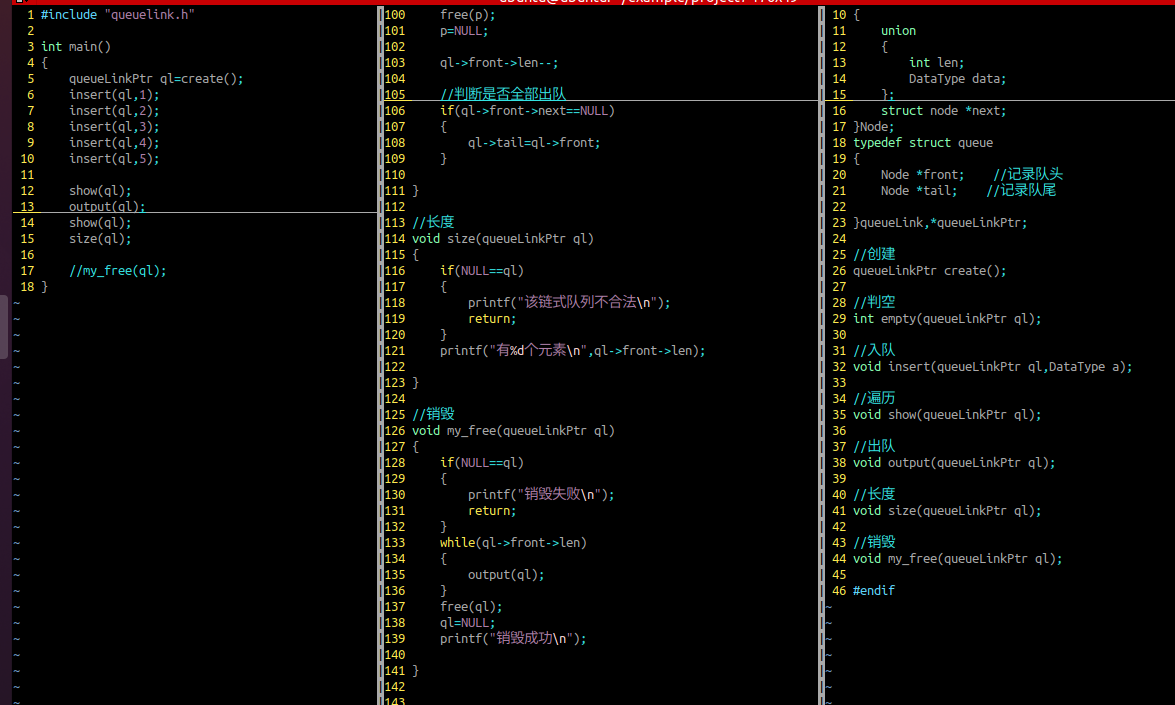
销毁
参数列表:顺序队列
判断申请空间是否合法
需要判空
树形结构:数据元素存在一对多的关系
二叉树
每个节点最多拥有两个子节点,并且有严格的左右子树区分的树形结构
二叉树的相关概念
左子树:以当前节点的左孩子节点为根节点的子树,称为左子树。
右子树:以当前节点的右孩子节点为根节点的子树,称为右子树。
左斜树:每个节点只有左孩子节点,没有右孩子节点的树,称为左斜树。
右斜树:每个节点只有右孩子节点,没有左孩子节点的树,称为右斜树。
满二叉树:在不增加层次的基础上,不能在往树上增加节点。
完全二叉树:在满二叉树的基础上,从左往右依次增加节点的树,称为完全二叉树。
二叉树的相关概念
1、在第i层上,最多有2^(i-1)个节点
2、在第K层上,最多总共拥有 2^K-1 节点
3、在一个树上,度为0的节点(叶子节点)总比度为2的节点个数多一个。
总节点个数 = 总度数 +1;
// n0 度0 n1 度1 n2 度2
n0+n1+n2 = 1*n1 + 2*n2 + 1
n0 + n1 + n2 = n1 + 2n2 +1
n0 = n2 +1二叉树的存储
满二叉树或者完全二叉树可以采用顺序存储,普通二叉树一般采用链式存储