机器学习课程学习周报六

摘要

本周的学习内容主要围绕循环神经网络（RNN）及其变体展开，包括简单循环神经网络、Elman网络、Jordan网络、双向循环神经网络（Bi-RNN）和长短期记忆网络（LSTM）。我详细讨论了每种网络的结构和工作原理，特别是LSTM的门机制及其在处理梯度消失的优势。通过具体的例子和数学推导，我深入理解了这些网络在实际应用中的操作过程和效果。

Abstract

This week, I focus on recurrent neural networks (RNNS) and their variants, including simple recurrent neural networks, Elman networks, Jordan networks, Bi-directional recurrent neural networks (Bi-RNNs), and Long Short-Term memory networks (LSTM). I discuss the structure and workings of each network in detail, especially the gate mechanism of LSTM and its advantages in dealing with vanishing gradients. Through specific examples and mathematical derivation, I deeply understand the operation process and effect of these networks in practical applications.

一、机器学习部分

1.1 循环神经网络概述

循环神经网络（Recurrent Neural Network, RNN）是带有记忆的神经网络，每一个隐藏层中的神经元产生输出的时候，该输出会被存到记忆元（memory cell），在下一次输入时，这些神经元不仅会考虑新的输入也会考虑记忆元中的值，从而影响神经网络的输出。

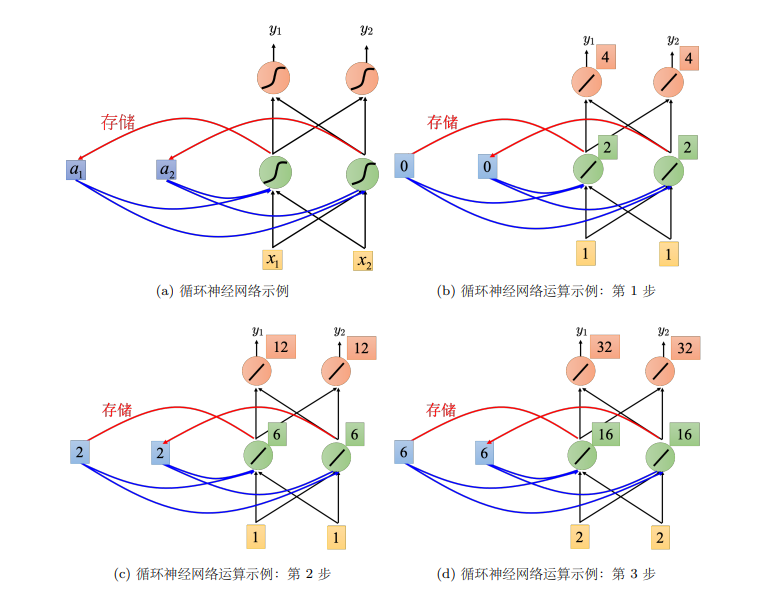
以上图为例，首先假设循环神经网络中所有的权重都是1，所有的神经元没有任何的偏置。输入序列是：${\left[1,1\right]}^{\mathrm{T}}$，${\left[1,1\right]}^{\mathrm{T}}$，${\left[2,2\right]}^{\mathrm{T}}$。在第1步中，绿色的隐藏层接入了输入的${\left[1,1\right]}^{\mathrm{T}}$，还接入了记忆元的${\left[0,0\right]}^{\mathrm{T}}$，绿色影藏层的输入就是2。接下来，循环神经网络会将绿色神经元的输出存在记忆元中，所以记忆元中的值被更新为2。在第2步中，同样要考虑输入的${\left[1,1\right]}^{\mathrm{T}}$和已更新的记忆元，因此绿色隐藏层的输出是6。以此类推，第3步中绿色隐藏层的输出是16。

1.2 循环神经网络架构

1.2.1 深层循环神经网络

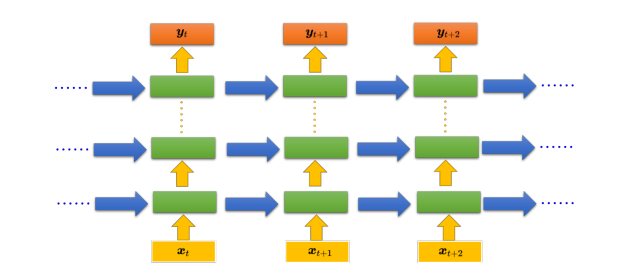
循环神经网络的架构是可以任意设计的，之前提到的 RNN 只有一个隐藏层，但 RNN 也 可以是深层的。比如把$x_t$丢进去之后，它可以通过一个隐藏层，再通过第二个隐藏层，以此类推 (通过很多的隐藏层) 才得到最后的输出。每一个隐藏层的输出都会被存在记忆元里面， 在下一个时间点的时候，每一个隐藏层会把前一个时间点存的值再读出来，以此类推最后得到输出，这个过程会一直持续下去。

1.2.2 Elman网络和Jordan网络

循环神经网络会有不同的变形，刚才介绍的是简单循环网络（Simple Recurrent Network, SRN），即把隐藏层的值存起来，在下一个时间点再读出来，这种网络也叫Elman网络。另外还有一种Jordan网络，它存的是整个网络输出的值，它把输出值在下一个时间点再读进来，把输出存到记忆元里。Elman网络没有目标，很难控制说它能学到什么隐藏层信息（学到什么就放到记忆元里），但是 Jordan网络是有目标，比较很清楚记忆元存储的东西。

1.2.3 双向循环神经网络

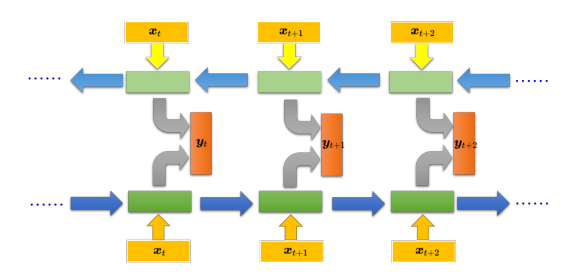
循环神经网络还可以是双向的。假设句子里的每一个单词用$x_t$表示，从句首一直读到句尾是先读$x_t$，再读$x_{t+1}$、$x_{t+2}$。但是也可以改变读取方向，如上图所示，先读$x_{t+2}$，再读$x_{t+1}$，最后读$x_t$。即我们可以同时训练一个正向 的循环神经网络，又可以训练一个逆向的循环神经网络，然后把这两个循环神经网络的隐藏层拿出来，分别接给一个输出层得到$y_t$、$y_{t+1}$、$y_{t+2}$，这种网络叫做双向循环神经网络（Bidirectional Recurrent Neural Network，Bi-RNN）。这种网络的神经元看的范围比较广，双向循环神经网络在产生$y_{t+1}$时，同时看$x_1$到$x_{t+1}$的输入和句尾到$x_{t+1}$的输入，因此网络等于看了整个句子后，才决定了每一个输出。

还有一种循环神经网络是长短期记忆网络，比较重要，单独开一节进行介绍。

1.3 长短期记忆网络

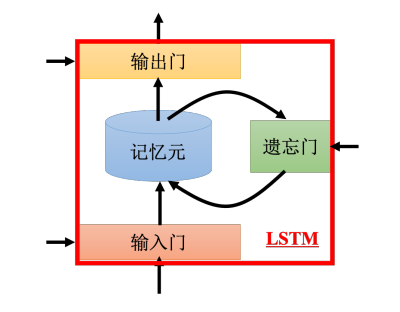
最常用的循环神经网络是长短期记忆网络（Long Short-Term Memory network，LSTM），长时间的短期记忆。LSTM有三个门（gate），当外界某个神经元的输入想要 被写到记忆元里面的时候，必须通过一个输入门（input gate），输入门要被打开的时候，才能把值写到记忆元里面。输出的地方也有一个输出门（output gate），输出门会决定外界其他的神经元能否从这个记忆元里面把值读出来。第三个门称为遗忘门（forget gate），遗忘门决定什么时候记忆元要把过去记得的东西忘掉。这三个门的打开关闭都是网络自己学到的。整个LSTM可以看成有 4 个输入、1个输出。在这4个输入中，一个是想要被存在记忆元的值，但不一定能存进去，还有操控输入门的信号、操控输出门的信号、操控遗忘门的信号，有这四个输入但它只会得到一个输出。

下面推导LSTM的输出：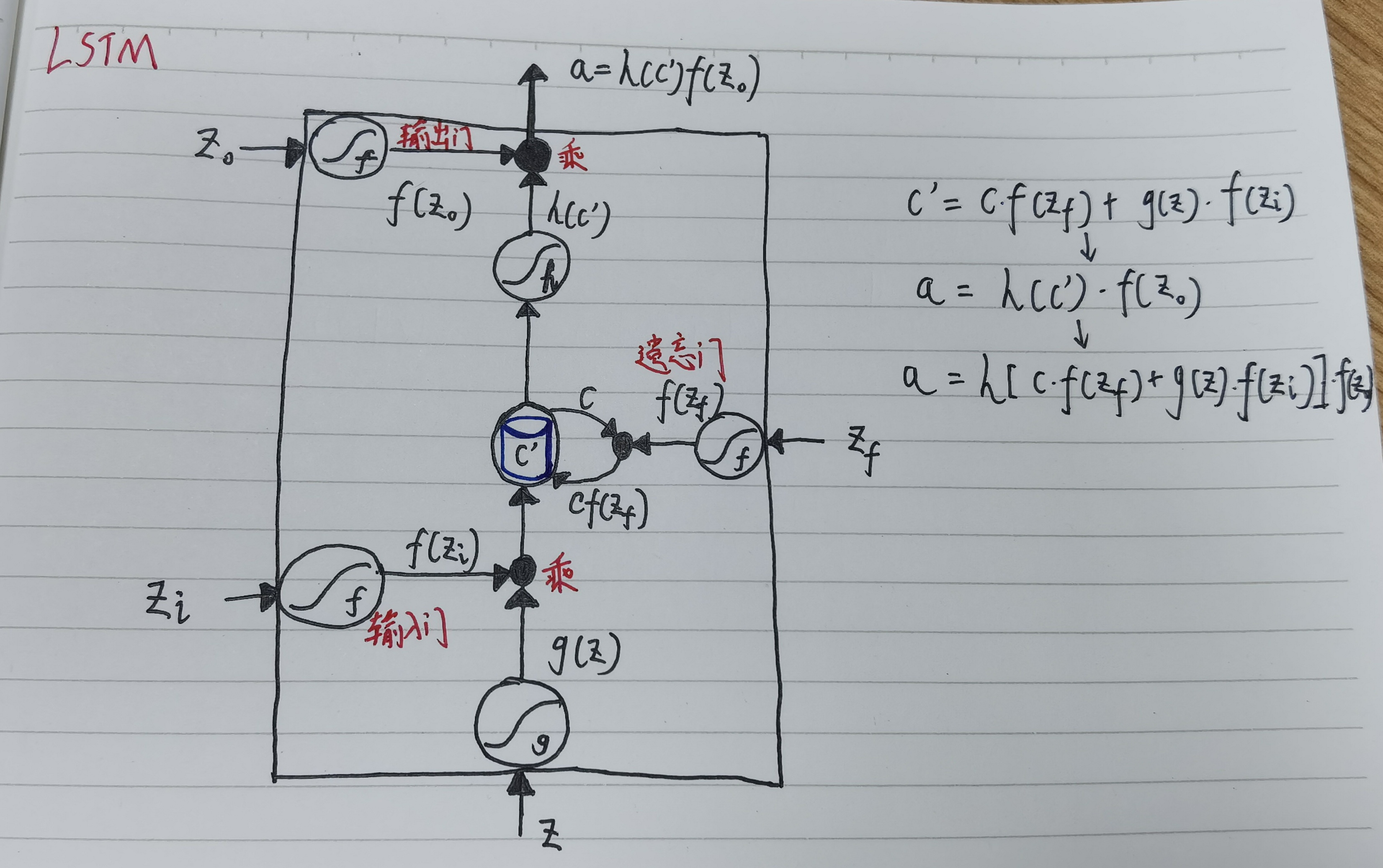

而实际中LSTM每个输入是这样组成的：先输入一个三维向量乘以线性变换（linear transform）。所得到的结果$x_1$，$x_2$，$x_3$乘以权重再加上偏置。底下这个外界传入的单元，$x_1$乘以1，其他的向量乘以 0，所以就直接把$x_1$当做输入。在输入门时，$x_2$乘以 100，偏置乘以 −10。假设$x_2$是没有值的话，通常输入门是关闭的（偏置等于 −10）。 因为−10通过sigmoid函数之后会接近0，所以就代表是关闭的，若$x_2$的值大于 1 的话，结果会是一个正值，代表输入门会被打开。遗忘门通常会被打开的，因为其偏置等于 10，它平 常会一直记得东西，只有当$x_2$的值为一个很大的负值时，才会把遗忘门关起来。输出门平常是被关闭的，因为偏置是一个很大的负值，若$x_3$ 有一个很大的正值的话，压过偏置就会把输出打开。

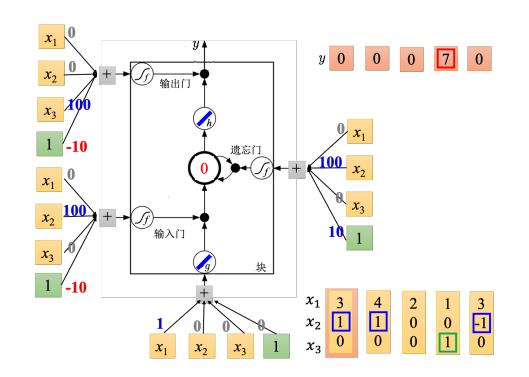
如下图中，输入的第一个向量是${\left[3,1,0\right]}^{\mathrm{T}}$，输入这边是$3\ast 1=3$，这边输入值为 3。输入门这边$\left(1\ast 100-10\approx 1\right)$是被打开 (输入门约等于1)，所以$\left(g\left(z\right)\ast f\left(z_i\right)=3\right)$。遗忘门$\left(1\ast 100+10\approx 1\right)$是被打开的 (遗忘门约等于1)，$0\ast 1+3=3=c\prime =g\left(z\right)f\left(z_i\right)+cf\left(z_f\right)$，所以存到记忆元里面的为 3。输出门 (-10) 是被关起来的，所以 3 无关通过，所以输出值为 0。

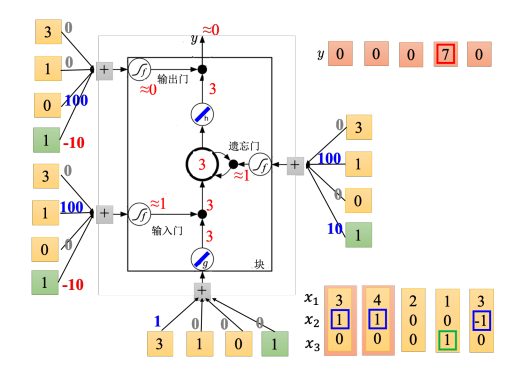
如下图，输入的第二个向量是${\left[4,1,0\right]}^{\mathrm{T}}$，传入输入的值为 4，输入门会被打开，遗忘门也会被打开，所以记忆元里面存的值等于 7（$3+4=7$），输出门仍然会被关闭的，所以 7 没有 办法被输出，所以整个记忆元的输出为 0。

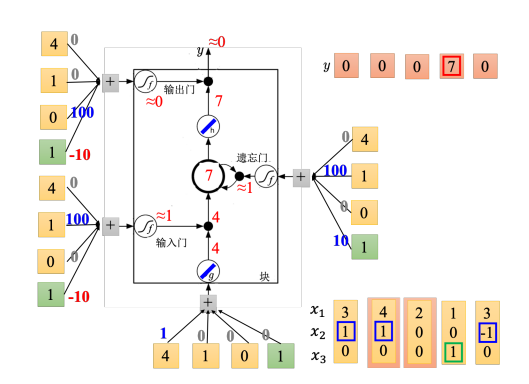
如下图，输入的第三个向量是${\left[2,0,0\right]}^{\mathrm{T}}$，传入输入的值为 2，输入门关闭，输入被输入门给挡住了，遗忘门打开。原来记忆元里面的值还是 7，输出门仍然为 0，所以没有办法输出，所以整个输出还是 0。

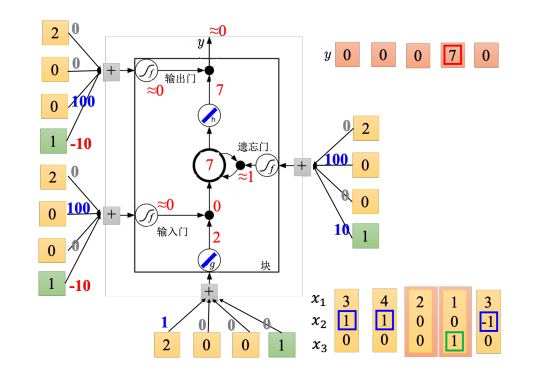
如下图，输入的第四个向量是${\left[1,0,1\right]}^{\mathrm{T}}$，传入输入的值为1，输入门是关闭的，遗忘门是打开的，记忆元里面存的值不变，输出门被打开，整个输出为 7，记忆元里面存的 7 会被读取出来。

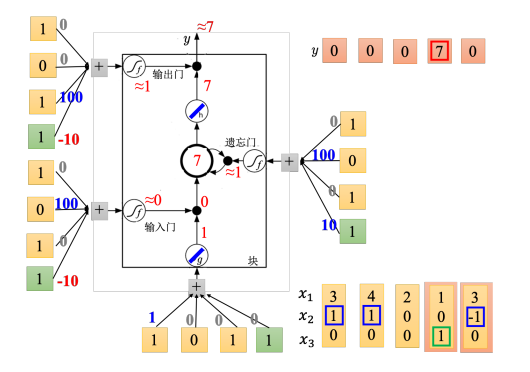
如下图，最后输入${\left[3,-1,0\right]}^{\mathrm{T}}$，传入输入的值为 3，输入门关闭，遗忘门关闭，记忆元里面的值会被洗掉变为0，输出门关闭，所以整个输出为0。

1.4 LSTM原理

在以往学习过的神经网络中，会有很多的神经元，我们会把输入乘以不同的权重当做不同神经元的输入，每一个神经元都是一个函数，现在我们把一个LSTM就当做一个神经元。

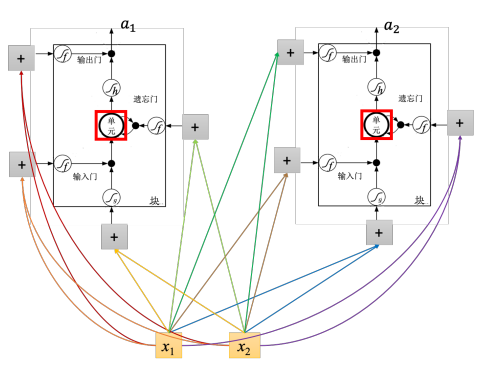
为了简化，假设隐藏层只有两个神经元，输入$x_1$,$x_2$会乘以不同的权重当做LSTM不同的输入。输入$x_1$,$x_2$会乘以不同的权重会去操控输出门，乘以不同的权重操控输入门，乘以不同的权重当做底下的输入，乘以不同的权重当做遗忘门。在原来的神经网络里是一个输入一个输出。在 LSTM 里面它需要四个输入，它才能产生一个输出。假设用的神经元的数量跟 LSTM 是一样的，则 LSTM 需要的参数量是一般神经网络的四倍。

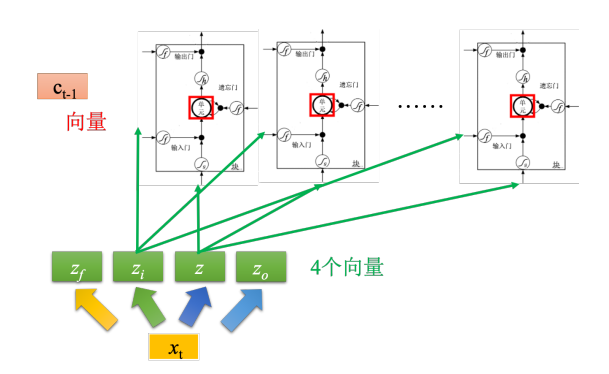
假设有一整排的 LSTM，这些 LSTM 里面的记忆元都存了一个值，把 所有的值接起来就变成了向量，写为$c_{t-1}$（一个值就代表一个维度）。现在在时间点$t$，输入向量 $x_t$，这个向量首先会乘上一个矩阵（线性变换）变成一个向量$z$，向量$z$的维度就代表了操控每一个 LSTM 的输入。$z$这个维度正好就是 LSTM 记忆元的数量。$z$的第一维就丢给第一个单元，第二维会丢给第二个单元，直到最后一维丢给最后一个单元。这个$x_t$会乘上另外的一个变换得到$z_i$，然后这个$z_i$的维度也跟单元的数量一 样，$z_i$的每一个维度都会去操控输入门。遗忘门跟输出门也都是一样，不再赘述。所以我们把$x_t$乘以四个不同的变换得到四个不同的向量，四个向量的维度跟单元的数量一样，这四个向量合起来就会去操控这些记忆元运作，因此所有LSTM单元是可以一起被运算的。

门控循环单元（Gated Recurrent Unit，GRU）是 LSTM 稍微简化的版本，它只有两个门。虽然少了一个门，但其性能跟 LSTM 差不多，少了 1/3 的参数，也是比较不容易过拟合。

1.5 RNN的学习方式

RNN的损失函数可以定义为交叉熵，对于训练也是用梯度下降来做。循环神经网络里面，为了要计算方便，提出了反向传播的进阶版，即随时间反向传播（BackPropagation Through Time，BPTT）。BPTT 跟反向传播其实是很类似的，只是循环神经网络它是在时间序列上运作，所以 BPTT 它要考虑时间上的信息。

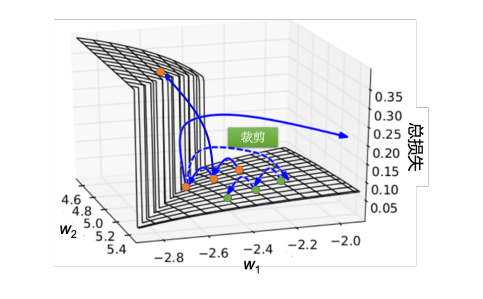
RNN 的误差表面的变化是非常陡峭的。误差表面有一些地方非常平坦，一些地方非常陡峭。纵轴是总损失，x 和 y 轴代表是两个参数。假设我们从橙色的点当做初始点，用梯度下降开始调整参数，更新参数， 可能会跳过一个悬崖，这时候损失会突然爆长，损失会非常上下剧烈的震荡。有时候可能我们一脚踩到这个悬崖上，在悬崖上的梯度很大，之前的梯度会很小，可能把学习率调的比较大。很大的梯度乘上很大的学习率结果参数就更新很多，整个参数就飞出去了。裁剪（clipping）可以解决该问题，当梯度大于某一个阈值的时候，不要让它超过那个阈值，比如当梯度大于15时，让梯度等于 15 结束。因为梯度不会太大，所以我们要做裁剪的时候，就算是踩着这个悬崖上，也不飞出来，会飞到一个比较近的地方，这样还可以继续做RNN的训练。

1.6 RNN中的梯度消失和梯度爆炸

梯度消失（Vanishing Gradient）来源于Sigmoid激活函数，Sigmoid函数的输出范围在（0,1）之间，具有平滑的、连续的性质。然而，Sigmoid函数的导数具有一个特性，即在输入很大或很小的情况下，其导数会趋近于零。这意味着在深度神经网络中，当梯度通过多个层反向传播时，多次使用Sigmoid函数作为激活函数会导致梯度逐渐变小，最终消失到接近零的程度，从而造成梯度消失问题。

在RNN中如果我们把激活函数换成ReLU，训练的效果仍然不佳，所以激活函数不是关键点。这里举一个RNN的简单例子，来说明梯度的问题。假设只有有一个神经元，这个神经元是线性的。输入没有偏置，输入的权重是 1，输出的权重也是 1， 转移的权重是 w。也就是说从记忆元接到神经元的输入的权重是 w。假设 w 是要学习的参数，我们想要知道它的梯度，所以改变 w 的值，观察其对对神经元的输出有多大的影响。如下图所示，误差表面很崎岖，梯度是时大时小的， 在非常小的区域内，梯度有很多的变化。

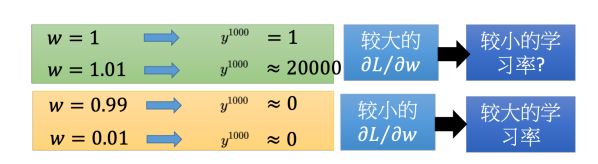
从这个例子可以看出 只要w一有变化，就会影响很大，梯度会很大或很小。所以 RNN 不好训练的原因不是来自激活函数而是来自于它有时间序列，同样的权重在不同的时间点被反复地使用。

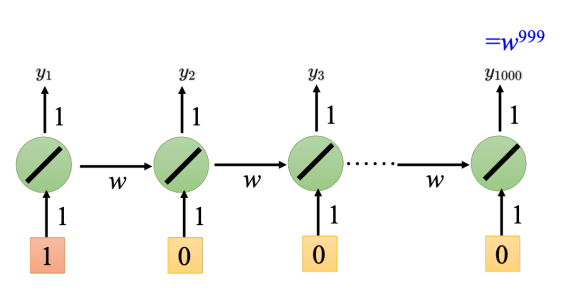
使用LSTM可以避免梯度过小，从而解决梯度消失（Vanishing Gradient）的问题，而不能解决梯度爆炸 （gradient exploding）的问题。

RNN 跟 LSTM 中记忆元的操作其实是不一样的，在 RNN 里面，在每一个时间点，神经元的输入都要放到记忆元里面，记忆元里面的值都是会被覆盖掉。但是在 LSTM 里面不 一样，它是把原来记忆元里面的值乘上一个值再把输入的值加起来放到记忆元里面，所以它的记忆和输入是相加的。LSTM 和 RNN 不同的是，如果权重可以影响到记忆元里面的值，一旦发生影响会永远都存在。而 RNN 在每个时间点的值都会被格式化掉，所以只要这个影响被格式化掉它就消失了。但是在 LSTM 里面，除非遗忘门要把记忆元的值替换掉。不然记忆元一旦有改变，只会把新的东西加进来，不会把原来的值洗掉，所以它不会有梯度消失的问题。

因此使用LSTM时，避免了梯度过小，大部分地方变化的很剧烈，在面对梯度爆炸问题时，可以把学习率设置的小一点，保证在学习率很小的情况下进行训练。

总结

在学习完RNN和Self-attention机制后，梳理清楚了它们之间的来龙去脉，在在下一周将进入Transformer的学习。