给你一棵二叉树的根节点，返回该树的 直径 。

二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。

两节点之间路径的 长度 由它们之间边数表示。

示例 1：

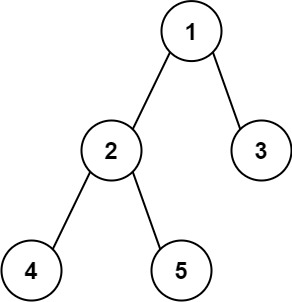
输入：root = [1,2,3,4,5]
输出：3
解释：3 ，取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。

示例 2：

输入：root = [1,2]
输出：1

提示：

• 树中节点数目在范围 [1, 104] 内
• -100 <= Node.val <= 100

知识点：

二叉树上的任一“路径”上一定有一个结点是所有其他结点的祖先结点（因为“路径”是由一个个父子关系连接而成的），那么换个表述方法，对于任一结点，以此结点为根的diameter就可以表示为左子树高度 + 右子树高度，而二叉树的diameter（直径）就是所有结点为根的diameter中最大的那个。 

思路：使用递归的方法，分别将每一个节点视为根节点，此时通过该节点的直径为左子树高度+右子树高度

在下图中，判断完节点2后要回溯到节点1继续判断，此时节点1的左子树高度为节点2的左子树高度和右子树高度中的最大值，再加1，即l(1)=max[ l(2) ,r(2)]+1,其中l(2)表示节点2的左子树高度

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
//将每一个节点分别看作根节点，两边最大高度相加得到的最大值即为直径
int find(TreeNode* root,int &max,int level){
    if(root==NULL)return 0;
    int l=find(root->left,max,level+1);
    int r=find(root->right,max,level+1);
    int d=r+l+1;

    if(d>max)max=d;
    return l>r? l+1:r+1;//最大直径+1
}
    int diameterOfBinaryTree(TreeNode* root) {
       int max=0;
       int level=0;
       int a=find(root,max,level);
       return max-1;

    }
};