有借鉴网上的部分
第一题
导入库,读取数据并且展示前五行(基本操作)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#读取数据
path = "./ex2data1.txt"
data = pd.read_csv(path,header=None,names=["exam1","exam2","accepted"])
print(data.head()) 可视化数据
可视化数据
将数据集绘制成散点图,这里采用了子图绘制的方式,返回的fig和ax对象分别代表了整个图形和其中的一个子图。x,y分别为每个样本的exam1和exam2,通过accepted区分蓝色和红色。
fig,ax=plt.subplots()
ax.scatter(data[data["accepted"]==0]["exam1"],data[data["accepted"]==0]["exam2"],c="r",marker="x")
ax.scatter(data[data["accepted"]==1]["exam1"],data[data["accepted"]==1]["exam2"],c="b",marker="o")
ax.set_xlabel('exam1')
ax.set_ylabel('exam2')
plt.show()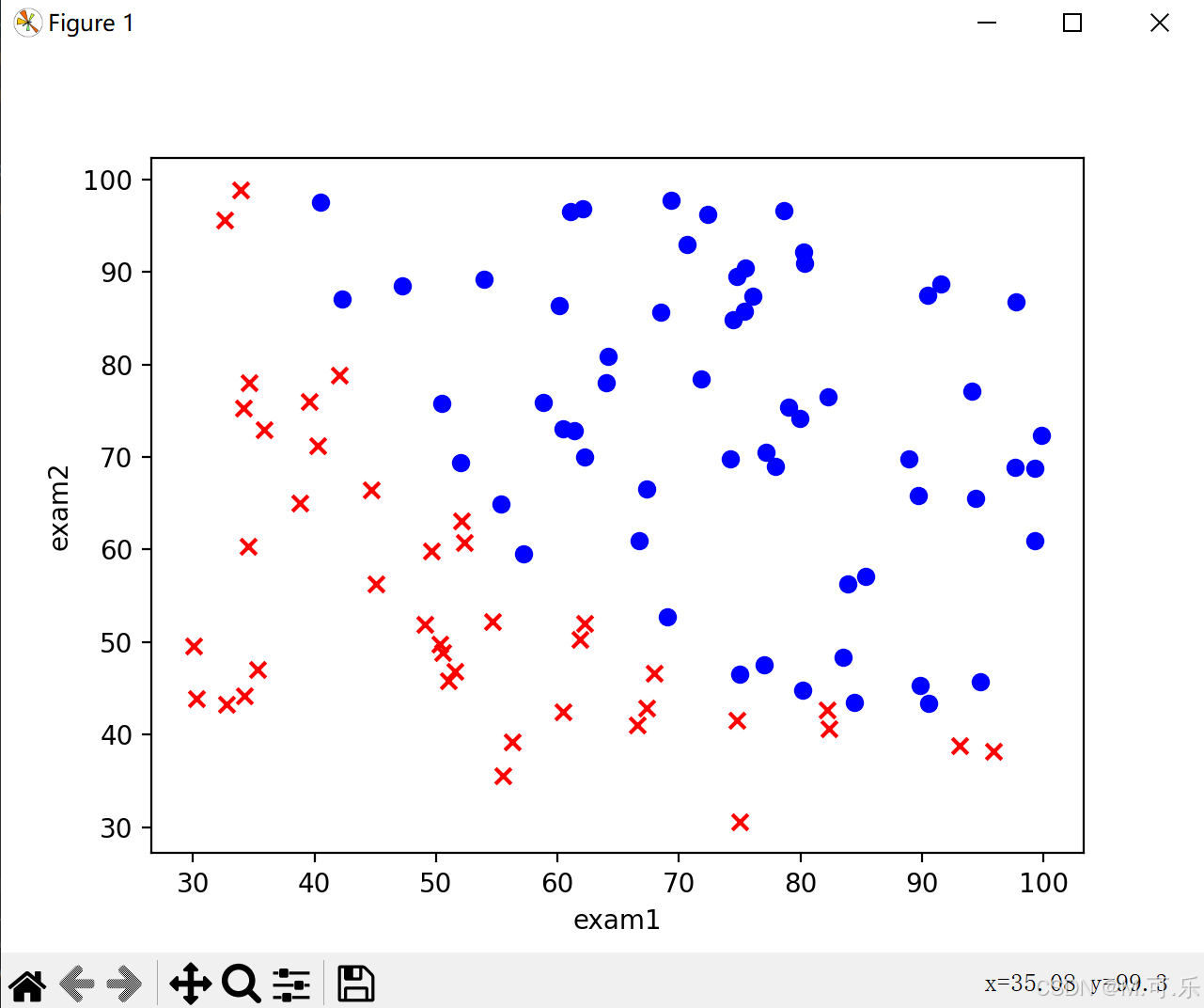
读取x,y
先添加一列为1,x为特征值,y为真实值
data.insert(0,"x0",1)
cols = data.shape[1]
x = data.iloc[:,0:cols-1]
y = data.iloc[:,cols-1:cols]
x = x.values
y = y.values.reshape(len(y), 1)
theta = np.zeros((3,1))构造损失函数
损失函数公式为
其中,
def cost_func(x,y,theta):
z = x@theta
A = 1/(1+np.exp(-z))
cost = -np.sum(y*np.log(A)+(1-y)*np.log(1-A))/len(x)
return cost构造梯度下降函数
def gradient_descent(x,y,theta,alpha,times):
m = len(x)
for i in range(times):
z = x@theta
A = 1/(1+np.exp(-z))
theta = theta - (alpha / m) * (x.T@(A-y))
cost = cost_func(x,y,theta)
pass
return theta初始化
alpha = 0.004
times = 200000
theta = gradient_descent(x,y,theta,alpha,times)决策界限
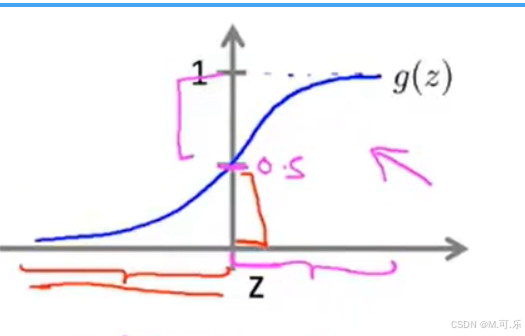
根据sigmoid函数(如图所示),当为边界线,也就是
。
所以,并且
为我们新添加的一列1,可以推出
所以
然后,绘制出图像,散点图和决策边界
conf1 = -theta[0,0]/theta[2,0]
conf2 = -theta[1,0]/theta[2,0]
x = np.linspace(20, 100, 100)
y = conf1+conf2*x
fig,ax=plt.subplots()
ax.scatter(data[data["accepted"]==0]["exam1"],data[data["accepted"]==0]["exam2"],c="r",marker="x")
ax.scatter(data[data["accepted"]==1]["exam1"],data[data["accepted"]==1]["exam2"],c="b",marker="o")
ax.plot(x,y,c="g")
ax.set_xlabel('exam1')
ax.set_ylabel('exam2')
plt.show() 第二题
第二题
导入库,读取数据并且展示前五行(基本操作)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#读取数据
path = "./ex2data2.txt"
data = pd.read_csv(path,header = None,names = ["exam1","exam2","accepted"])
print(data.head())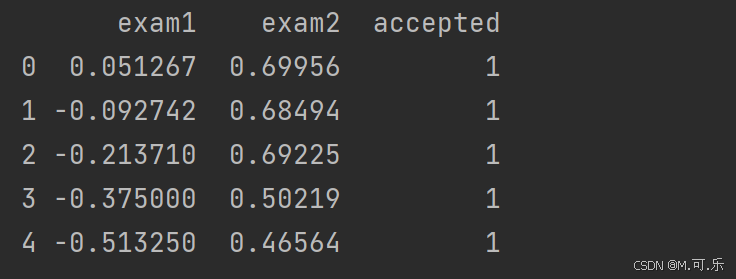
可视化数据
将数据集绘制成散点图,这里采用了子图绘制的方式,返回的fig和ax对象分别代表了整个图形和其中的一个子图。x,y分别为每个样本的exam1和exam2,通过accepted区分蓝色和红色。
fig,ax=plt.subplots()
ax.scatter(data[data["accepted"]==0]["exam1"],data[data["accepted"]==0]["exam2"],c="r",marker="x")
ax.scatter(data[data["accepted"]==1]["exam1"],data[data["accepted"]==1]["exam2"],c="b",marker="o")
ax.set_xlabel('exam1')
ax.set_ylabel('exam2')
plt.show()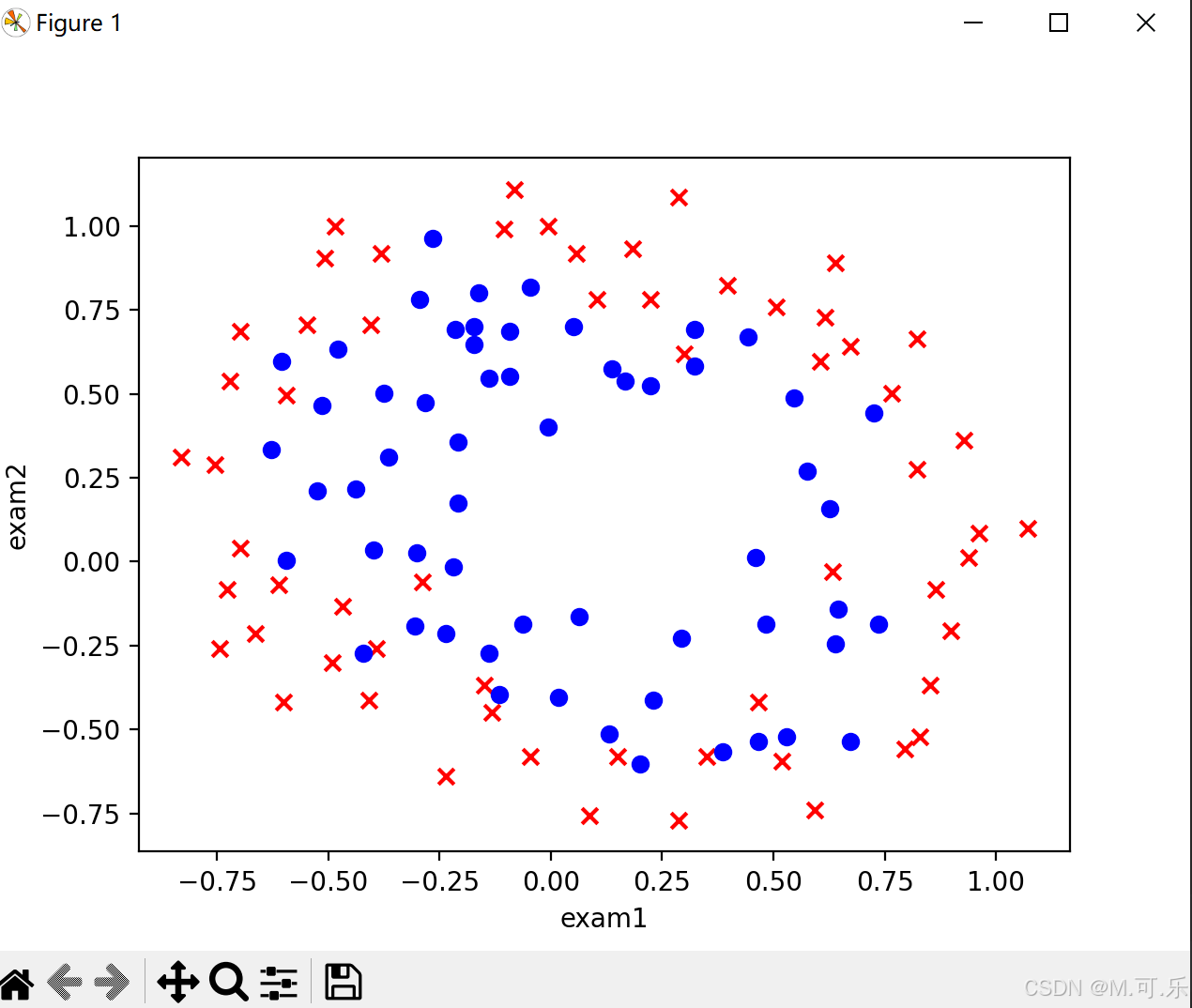
特征映射
通过上面绘制的散点图,我么可以看出来,该题目是线性不可分的,所以我们要增加项的次数,采用的是特征映射的方式
def feature_mapping(x1,x2,times):
data = {}
for i in range(times+1):
for j in range(i+1):
data["F{}{}".format(i-j,j)] = np.power(x1,i-j)*np.power(x2,j)
return pd.DataFrame(data)
x1 = data["exam1"]
x2 = data["exam2"]
data_finite = feature_mapping(x1,x2,6)读取x,y
因为在特征映射时,可以根据公式看出第一列已经为0
cols = data.shape[1]
x = data_finite.values
y = data.iloc[:,cols-1:cols]
y = y.values
theta = np.zeros((28,1))构造代价函数
跟第一题不同的是,这里要加入正则化,为了防止过拟合现象
def cost_func(x,y,theta,lamda):
z = x@theta
A = 1/(1+np.exp(-z))
m = len(x)
cost = np.sum(-y*np.log(A)-(1-y)*np.log(1-A))/m
reg = np.sum(np.power(theta[1:],2))*(lamda/2*m)
return cost+reg构造梯度下降函数
def gradient_descent(x, y, theta, alpha, iters, lamda):
for i in range(iters):
reg = theta[1:] * (lamda / len(x))
reg = np.insert(reg, 0, values=0, axis=0)
z = x @ theta
A = 1 / (1 + np.exp(-z))
# X.T:X的转置
theta = theta - (x.T @ (A - y)) * alpha / len(x) - reg*alpha
cost = cost_func(x, y, theta, lamda)
return theta初始化
alpha = 0.001
times = 200000
lamda = 0.01
theta = gradient_descent(x,y,theta,alpha,times,lamda)决策界限
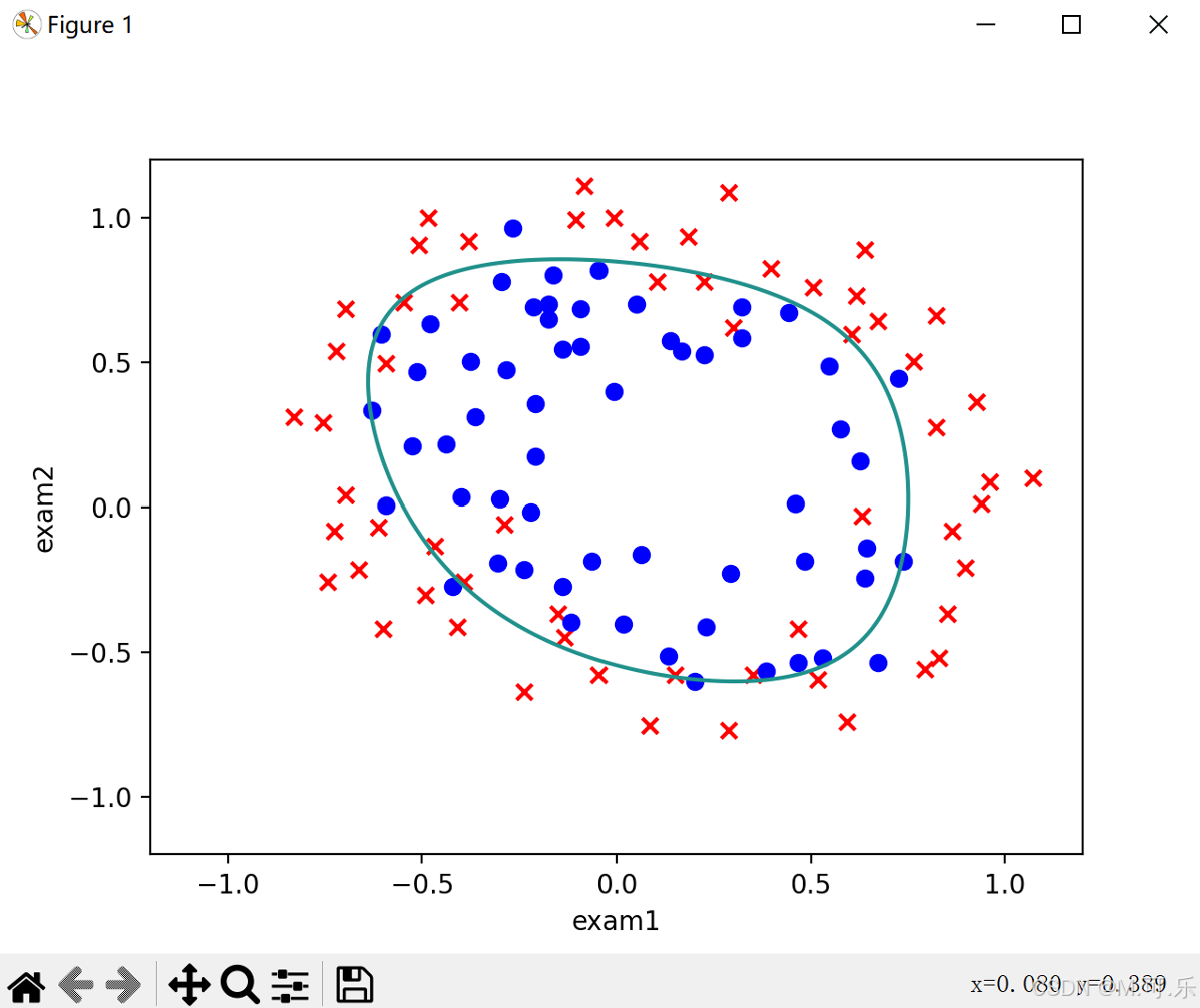
这里我么需要画出决策界限(非线性)
首先,我们先调用meshgrid函数,得到网格中的坐标对应的x,y值。
x = np.linspace(-1.2, 1.2, 200)
X,Y = np.meshgrid(x,x)
z = feature_mapping(X.ravel(), Y.ravel(), 6).values
Z = z @ theta
Z = Z.reshape(X.shape)
fig, ax = plt.subplots()
ax.scatter(data[data['accepted'] == 0]['exam1'], data[data['accepted'] == 0]['exam2'], c='r', marker='x')
ax.scatter(data[data['accepted'] == 1]['exam1'], data[data['accepted'] == 1]['exam2'], c='b', marker='o')
ax.set_xlabel('exam1')
ax.set_ylabel('exam2')
plt.contour(X, Y, Z, 0)
plt.show()