给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

示例 1：

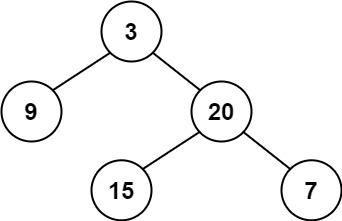
输入：root = [3,9,20,null,null,15,7]

输出：true

示例 2：

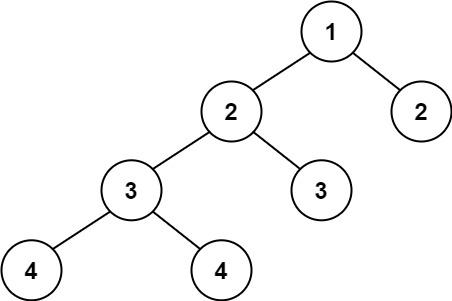
输入：root = [1,2,2,3,3,null,null,4,4]

输出：false

示例 3：

输入：root = []

输出：true

提示：

• 树中的节点数在范围 [0, 5000] 内

• -104 <= Node.val <= 104

110. 平衡二叉树 - 力扣（Leetcode）

思路：

回顾一下，什么是高度平衡二叉树？二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
那么我们遍历一下二叉树的每个节点，只有当所有节点均满足左右两个子树的高度差的绝对值不超过 1 时，才能满足题目要求。
定义函数 height 用于获取以当前节点为根的二叉树的高度 ，若是左子树不为平衡二叉树或者右子树不为平衡二叉树或者左子树与右子树的差大于 1，则说明该二叉树不是平衡二叉树，返回 -1，否则正常返回二叉树的高度值 = 左子树与右子树最大高度 + 1

c++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isBalanced(TreeNode* root) {
        return height(root) >= 0;
    }

    // 返回当前节点的最大高度，若是不为平衡二叉树，则返回 -1
    int height(TreeNode* root) {
        if(root == nullptr) {
            return 0;
        }

        int leftHeight = height(root->left);
        int rightHeight = height(root->right);
        
        // 若是左子树不为平衡二叉树或者右子树不为平衡二叉树或者左子树与右子树的差大于 1，则说明该二叉树不是平衡二叉树，返回 -1
        if(leftHeight == -1 || rightHeight == -1 || abs(leftHeight - rightHeight) > 1) {
            return -1;
        }

        return max(leftHeight, rightHeight) + 1;
    }
};