最近有个需求，需要对一个S曲线的散点图做线性拟合，百度上线性拟合和曲线拟合公式很多，没什么问题，但需求里面有一个预期就是自动找出直线部分，前面因为其它事情耽搁，一直没有实现，心里多少有点梗。

1.线性拟合算法

这个是百度上找到的，个人认为还可以

void calculate(double *x,double *y,uint32_t size,float *slop,float *Intercept)
{
    float fXY = 0, fXX = 0, fXA = 0, fYA = 0, fYY = 0;
    //得到平均值
    for(int i = 0;i < size;i++)
    {
        fXA += x[i]/size;
        fYA += y[i]/size;
    }
    //得到拟合所必需的数据
    for(int i = 0;i < size;i++)
    {
        fXY  += (x[i] - fXA)*(y[i] - fYA);
        fXX += (x[i] - fXA)*(x[i] - fXA);
        fYY += (y[i] - fYA)*(y[i] - fYA);
    }
    *slop = fXY / fXX;
    *Intercept = fYA - ((*slop) * fXA);
}

这是我测试的结果：y=1.40467x-975.062

这是第三方软件的测试结果：F(x) = 1.4046744537015599*x+-975.0620148430177

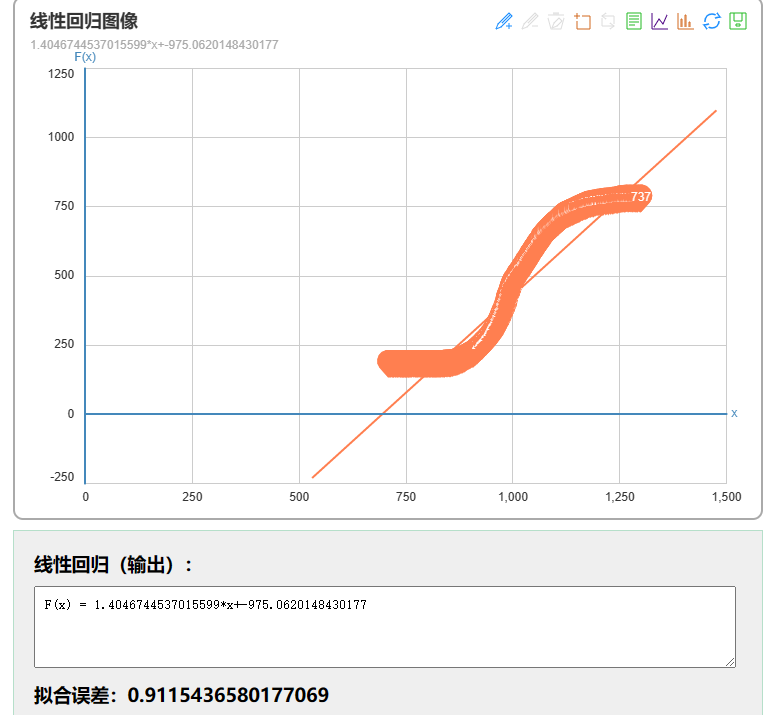
结果是一致的

2.找直线思路-先分段找斜率

这个是挺头疼的，网上文章也有一些，但大多数是一些理论性的，反正找了一段时间，没看到合适的

目前思路是这样的

对整个数据，分段拟合直线，再对斜率做方差，找出斜率变化最大的位置和最小的位置，取中间点作为曲线的拐点

S曲线上来看，斜率变化是有规律的，从小到大再变小，放到方差结果来看，猜测也是一样的结果

理想状态下的结果应该是下图的结果

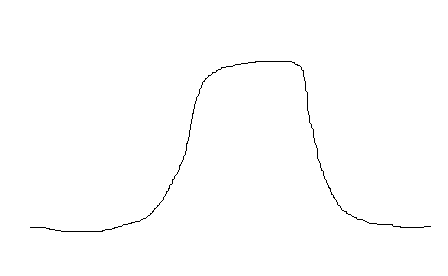
对方差结果绘图查看一下

1.从第一个数据开始，拿固定数据量，做线性拟合，比如第一次拿1~10个数据，第二次拿2~11个数据，以此类推，一直取到（size/2）-range个数据，size是总的数据量，range是每次拿的数据个数

2.从size/2开始，以同样方式，收集斜率

3.理想状态下，上图会被分成左右两半

斜率不能直接用，因为实际状态下，数据是散点图，如果range不够大，实际拟合的结果和下面类似

如果范围较宽，结果应该是这样的

黑色部分是按一定range拟合的曲线，虽然整体状态下是一个S曲线的趋势，但不管哪种，还是比较乱的，实际计算结果如下

从中间分开，每5个数据，拟合一个直线，将所有斜率打印出来

slop_f: 0 slop_b: 3.85714
slop_f: 0 slop_b: 3.21429
slop_f: 0 slop_b: 2.5
slop_f: 0 slop_b: 3
slop_f: 0 slop_b: 3.15385
slop_f: 0 slop_b: 3.30769
slop_f: 0 slop_b: 3.25
slop_f: 0 slop_b: 2.69231
slop_f: 0 slop_b: 2.38462
slop_f: 0.2 slop_b: 2.25
slop_f: 0.3 slop_b: 2.375
slop_f: 0.3 slop_b: 2.66667
slop_f: 0.2 slop_b: 3.41667
slop_f: 0.189189 slop_b: 3.33333
slop_f: 0.244186 slop_b: 3.27273
slop_f: 0.244186 slop_b: 2.31395
slop_f: 0.189189 slop_b: 2.06604
slop_f: 0 slop_b: 1.97368
slop_f: 0.2 slop_b: 1.82609
slop_f: 0.3 slop_b: 3.83333
slop_f: 0.22973 slop_b: 2.35714
slop_f: 0.139535 slop_b: 1.92308
slop_f: 0.121212 slop_b: 2.08824
slop_f: 0.23913 slop_b: 2.7
slop_f: 0.346154 slop_b: 2.43396
slop_f: 0.176471 slop_b: 2.60377
slop_f: 0.176471 slop_b: 2.78947
slop_f: 0.615385 slop_b: 3.04348
slop_f: 0.769231 slop_b: 3.11765
slop_f: 0.794118 slop_b: 2.45455
slop_f: 0.5 slop_b: 2.03488
slop_f: 0.608108 slop_b: 1.86486
slop_f: 0.672414 slop_b: 2
slop_f: 0.576923 slop_b: 2
slop_f: 0.424658 slop_b: 2.5625
slop_f: 0.263158 slop_b: 3.5
slop_f: 0.333333 slop_b: 4.5
slop_f: 0.517544 slop_b: 4.66667
slop_f: 0.833333 slop_b: 2.54167
slop_f: 0.804348 slop_b: 2.375
slop_f: 0.673913 slop_b: 2.58696
slop_f: 0.590909 slop_b: 2.32609
slop_f: 0.604651 slop_b: 3.92857
slop_f: 0.810811 slop_b: 4.16667
slop_f: 1 slop_b: 2.29167
slop_f: 1 slop_b: 2.41667
slop_f: 1 slop_b: 2.25
slop_f: 1 slop_b: 2.25
slop_f: 1.35294 slop_b: 4.5
slop_f: 1.54545 slop_b: 2.6875
slop_f: 1.80556 slop_b: 2.14706
slop_f: 1.91667 slop_b: 1.9
slop_f: 1.77273 slop_b: 2.08824
slop_f: 2.17647 slop_b: 2.69231
slop_f: 1.62162 slop_b: 1.95652
slop_f: 1.36047 slop_b: 2.13043
slop_f: 1.40351 slop_b: 2.09259
slop_f: 1.35616 slop_b: 2.11364
slop_f: 1.5 slop_b: 2.14706
slop_f: 1.41096 slop_b: 1.5
slop_f: 1.41096 slop_b: 1.55882
slop_f: 1.61538 slop_b: 1.92308
slop_f: 1.93103 slop_b: 2.92857
slop_f: 2.25 slop_b: 2.5
slop_f: 2.5 slop_b: 2.2963
slop_f: 2.63953 slop_b: 2.29688
slop_f: 1.81343 slop_b: 1.95
slop_f: 1.69403 slop_b: 2.4375
slop_f: 1.51942 slop_b: 2.2037
slop_f: 1.47573 slop_b: 2.20455
slop_f: 1.85075 slop_b: 2.11765
slop_f: 1.92453 slop_b: 2.29412
slop_f: 2.6 slop_b: 3.19231
slop_f: 2.8 slop_b: 3.92857
slop_f: 2.37838 slop_b: 4.35714
slop_f: 2.13953 slop_b: 3.78571
slop_f: 2.13953 slop_b: 2.5
slop_f: 2.37838 slop_b: 2.33333
slop_f: 2.6 slop_b: 2.41667
slop_f: 2.5 slop_b: 2.5
slop_f: 2.79412 slop_b: 4
slop_f: 3.30769 slop_b: 2.75
slop_f: 3.28261 slop_b: 2.75
slop_f: 3.07576 slop_b: 2.69231
slop_f: 3.07576 slop_b: 3.28571
slop_f: 3.28261 slop_b: 2.64286
slop_f: 2.63043 slop_b: 2.5
slop_f: 2.43939 slop_b: 2.71429
slop_f: 2.33721 slop_b: 2.85714
slop_f: 2.15 slop_b: 4
slop_f: 2.31395 slop_b: 2.5
slop_f: 2.33333 slop_b: 2
slop_f: 2.73913 slop_b: 2
slop_f: 2.60811 slop_b: 2.125
slop_f: 2.42857 slop_b: 3.75
slop_f: 2.38298 slop_b: 2.25
slop_f: 2.53191 slop_b: 2.16667
slop_f: 2.77273 slop_b: 2
slop_f: 2.04386 slop_b: 1.5
slop_f: 1.76027 slop_b: 1.5625
slop_f: 1.61538 slop_b: 1.75
slop_f: 1.7069 slop_b: 1.96154
slop_f: 2.14865 slop_b: 2.11538
slop_f: 2.3 slop_b: 2.25
slop_f: 2.55882 slop_b: 1.92308
slop_f: 2.92308 slop_b: 1.76923
slop_f: 3.35714 slop_b: 2.05882
slop_f: 5.16667 slop_b: 2
slop_f: 3.16667 slop_b: 2.29412
slop_f: 2.75 slop_b: 3
slop_f: 2.78261 slop_b: 2
slop_f: 2.61765 slop_b: 1.4375
slop_f: 5.5 slop_b: 1.5
slop_f: 3.5 slop_b: 1.875
slop_f: 3.66667 slop_b: 2.5
slop_f: 3 slop_b: 2.16667
slop_f: 2.85714 slop_b: 1.5
slop_f: 2 slop_b: 1.35714
slop_f: 1.81481 slop_b: 1.35714
slop_f: 1.84375 slop_b: 1.21429
slop_f: 1.86486 slop_b: 1.21429
slop_f: 2.79412 slop_b: 1.07692
slop_f: 3.6875 slop_b: 1.17647
slop_f: 4.5 slop_b: 1
slop_f: 4.5 slop_b: 0.8
slop_f: 2.78571 slop_b: 0.5
slop_f: 2.92857 slop_b: 0.2
slop_f: 3.35714 slop_b: 0
slop_f: 2.61538 slop_b: 0
slop_f: 2.75 slop_b: 0
slop_f: 2.38462 slop_b: 0
slop_f: 3.30769 slop_b: 0
slop_f: 2.85294 slop_b: 0.151163
slop_f: 2.3 slop_b: 0.22093
slop_f: 2.5 slop_b: 0.243243
slop_f: 1.84091 slop_b: 0.4
slop_f: 2.02778 slop_b: 0.3
slop_f: 2 slop_b: 0.3
slop_f: 1.625 slop_b: 0.2
slop_f: 2.5 slop_b: 0.189189
slop_f: 1.78571 slop_b: 0.244186
slop_f: 2.07143 slop_b: 0.201754
slop_f: 1.5 slop_b: 0.140351
slop_f: 1.57407 slop_b: 0
slop_f: 1.76087 slop_b: 0
slop_f: 1.85294 slop_b: 0
slop_f: 2.45833 slop_b: 0.111111

肉眼来看，和预期是一样的，前半段，斜率在上升，后半段，斜率在下降

斜率总体趋势能看出来，但不太好处理，这里考虑从方差入手，理想状态下，S曲线可以看作这样的

3.找直线思路-斜率计算方差，看变化程度

前半段方差绘制成曲线

后半段方差绘制成曲线

这段测试数据完整的方差曲线应该是这样的

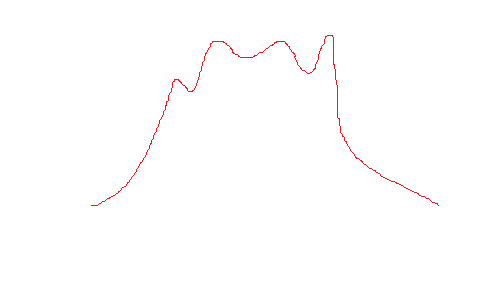
再看一下实际数据，两头平缓，方差上的值应该比较小，中间比较抖，因为数据并不是一个完全直线，所以在高处，是有点波动的

方差和曲线的对应关系应该是这样的

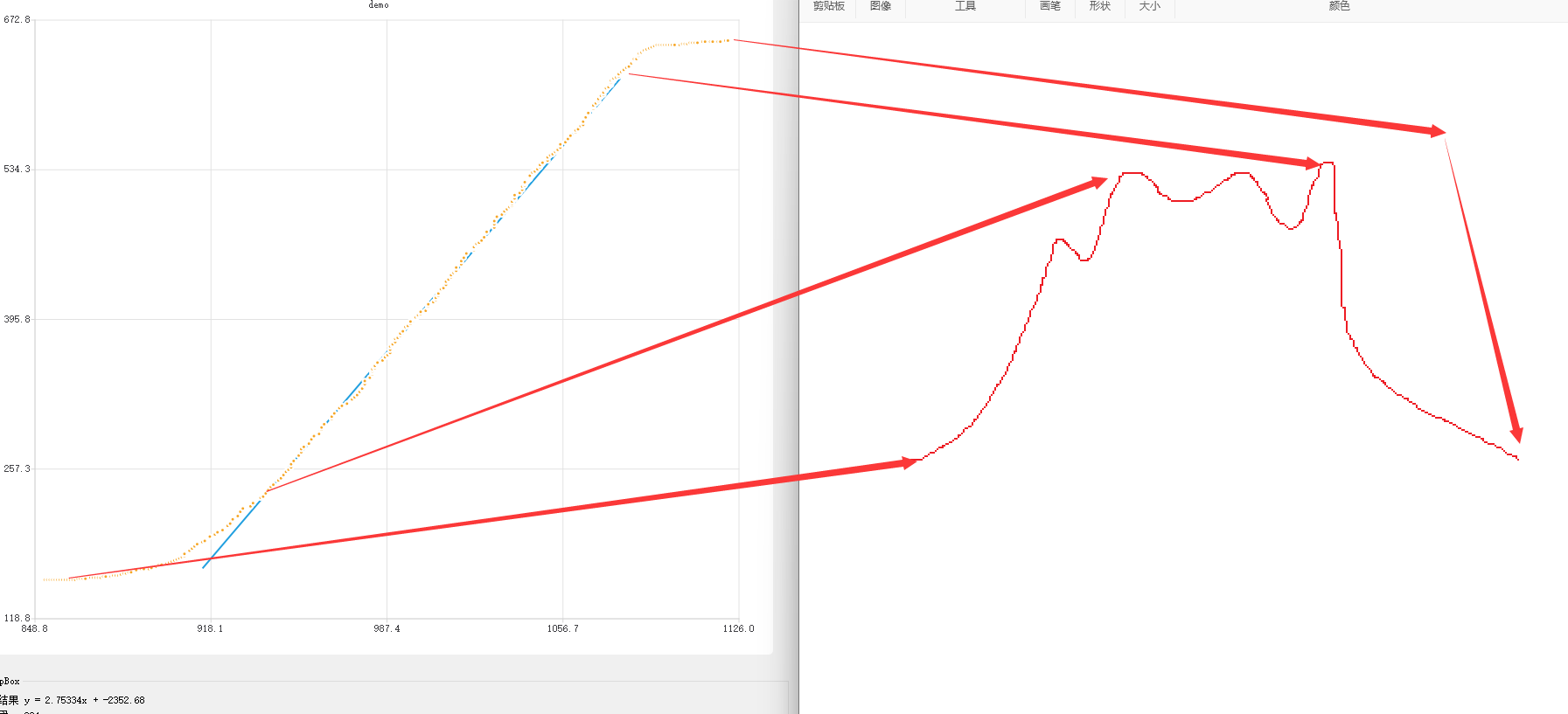
4.找直线思路-找出真实拐点

这里想了蛮久，怎么去找最真实的拐点，后面想通了，其实直接用方差的最大值减去方差的最小值，再除以2就是方差曲线的拐点，这个点也对应S曲线的拐点，误差肯定有，但对数据而言，误差应该是不会很大的

前半段拐点计算

double min_p = 0,max_p = 0;
double min_v = 0,max_v = 0;
double start_val = variance_f[0] > variance_f[1]?variance_f[0] - variance_f[1]:variance_f[1] - variance_f[0];
min_v = start_val;
max_v = start_val;
for(uint32_t i=0;i<variance_f.size()-1;i++)
{
    if(min_v > variance_f[i] || min_v == 0)
    {
    min_v = variance_f[i];
    min_p = i;
    }
    if(max_v < variance_f[i])
    {
        max_v = variance_f[i];
        max_p = i;
    }
}
//计算拟合位置
if(max_p > min_p)
    start = (max_p - min_p)/2 + min_p;
else
    start = (min_p - max_p)/2 + max_p;

后半段拐点计算

min_p = 0,max_p = 0;
    min_v = 0,max_v = 0;
    start_val = variance_b[0] > variance_b[1]?variance_b[0] - variance_b[1]:variance_b[1] - variance_b[0];
    min_v = start_val;
    max_v = start_val;
    for(uint32_t i=0;i<variance_b.size()-1;i++)
    {
        if(min_v > variance_b[i] || min_v == 0)
        {
            min_v = variance_b[i];
            min_p = i;
        }

        if(max_v < variance_b[i])
        {
            max_v = variance_b[i];
            max_p = i;
        }
    }
    if(max_p > min_p)
        end = size - (max_p - min_p)/2;
    else
        end = size - (min_p - max_p)/2;

5.影响因素

这里有一个关键的参数，就是每隔多少个数据，拟合曲线，数据量会决定光滑程度

比如每隔5个数拟合，后半段方差状态是这样的

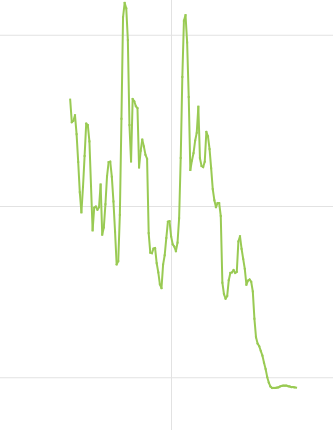
每隔20个数据，效果是这样的

这个貌似只能根据实际情况调整，没有固定的值

不过就最终结果而言，这个测试数据的影响好像差距不是很大

如以5个数据做拟合的话，结果如下

每隔20个数据的结果如下

直线方程f分别是y=2.75334x-2352.68和y=2.71389x-2311.79

6.测试异常情况

上面的曲线数据还比较近似S曲线，尝试对波动更大的情况做测试，这是取样范围是20的时候拟合出来的直线

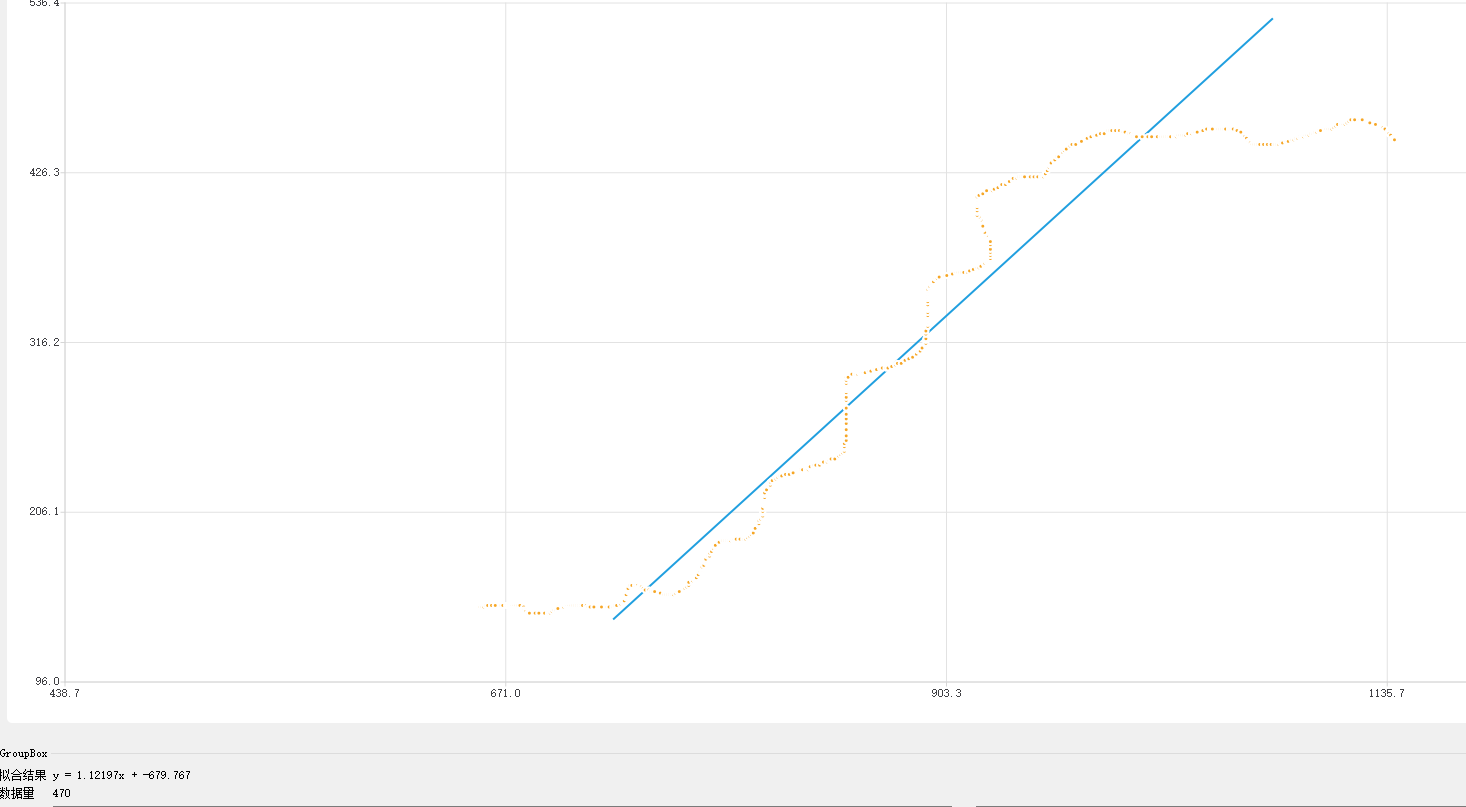
方差状态

如果取样范围是5，偏差会比较大

前后两段方差状态有点变态

再看看其它情况下的拟合结果

这是直线部分不稳定的情况，现在拟合的范围是5

这是拐点前后不稳定的情况

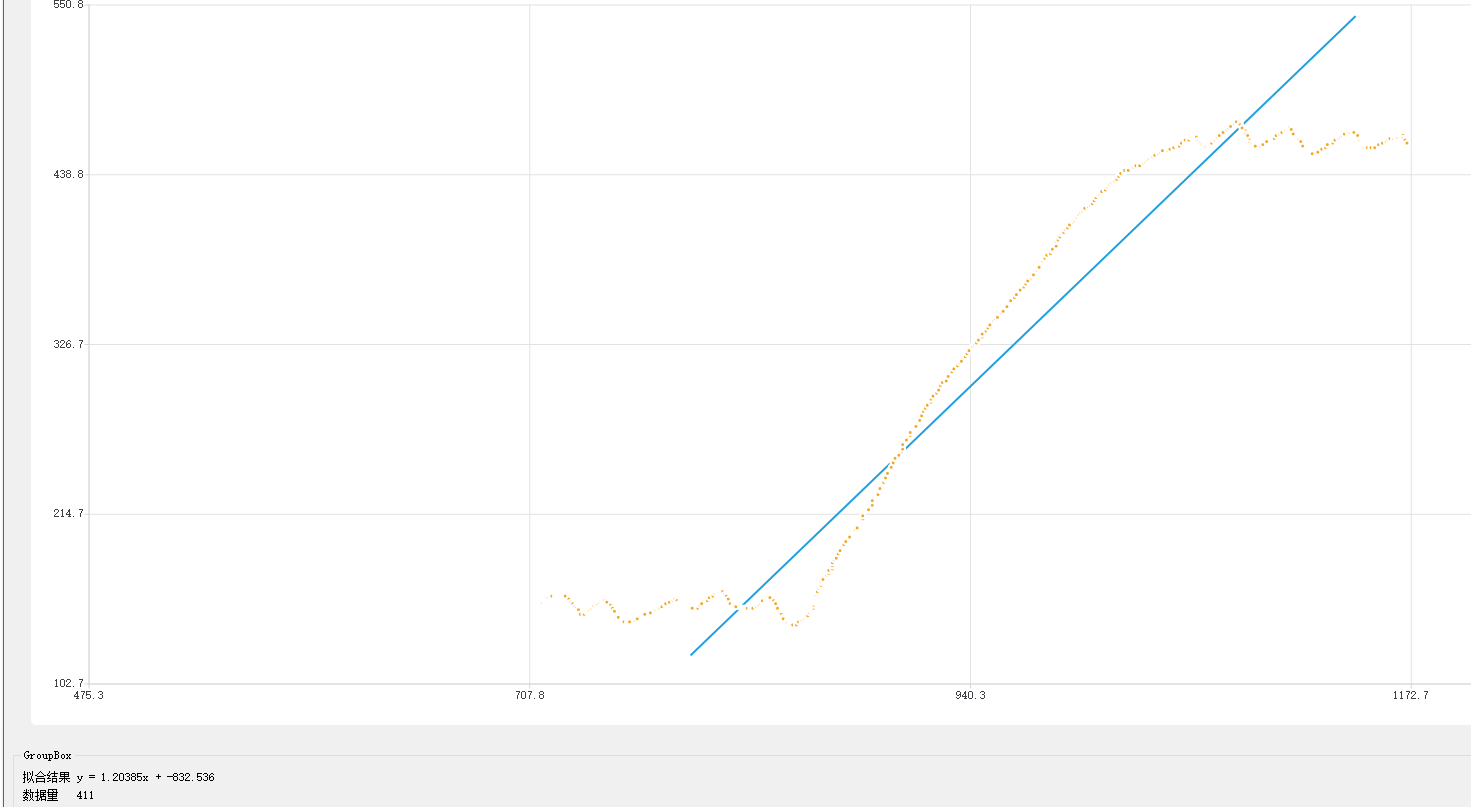
可以看出，影响程度来看，中间数据变动对拟合结果影响相对较小，两头不稳定影响程度是比较大的

查看这个时候的方差状态

当出现数据两头数据不稳定时，需要对更大范围的数据做拟合，来抑制影响