[LeetCode周赛复盘] 第 317 场周赛20221030
- 一、本周周赛总结
- 二、 [Easy] 6220. 可被三整除的偶数的平均值
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 三、[Medium] 6221. 最流行的视频创作者
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 四、[Medium] 6222. 美丽整数的最小增量
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 五、[Hard] 6223. 移除子树后的二叉树高度
- 1. 题目描述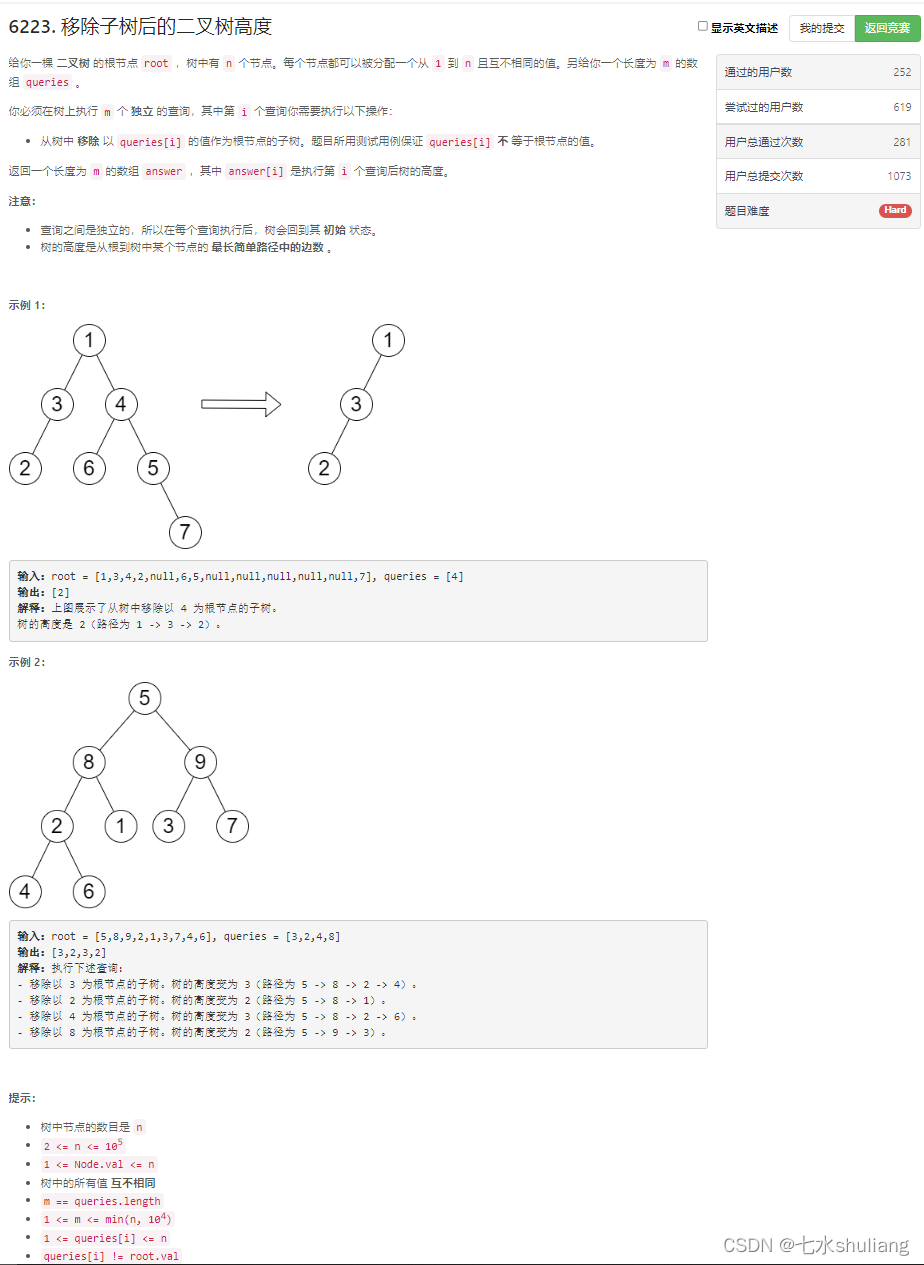
- 2. 思路分析
- 3. 代码实现
- 六、参考链接
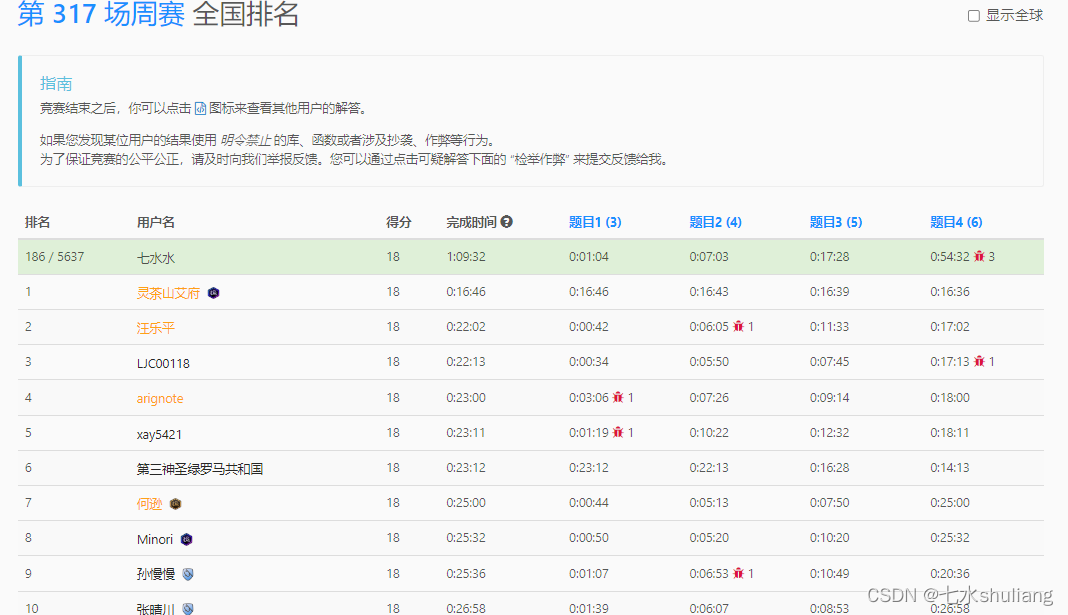
一、本周周赛总结
- 4题都挺难的。
- T4wa两次,最后没删打印导致了一次TLE。。
- T1 直接模拟。
- T2 统计和然后排序模拟。
- T3 贪心,从高位开始加模拟。
- T4 dfs然后哈希表统计。
二、 [Easy] 6220. 可被三整除的偶数的平均值
链接: 6220. 可被三整除的偶数的平均值
1. 题目描述
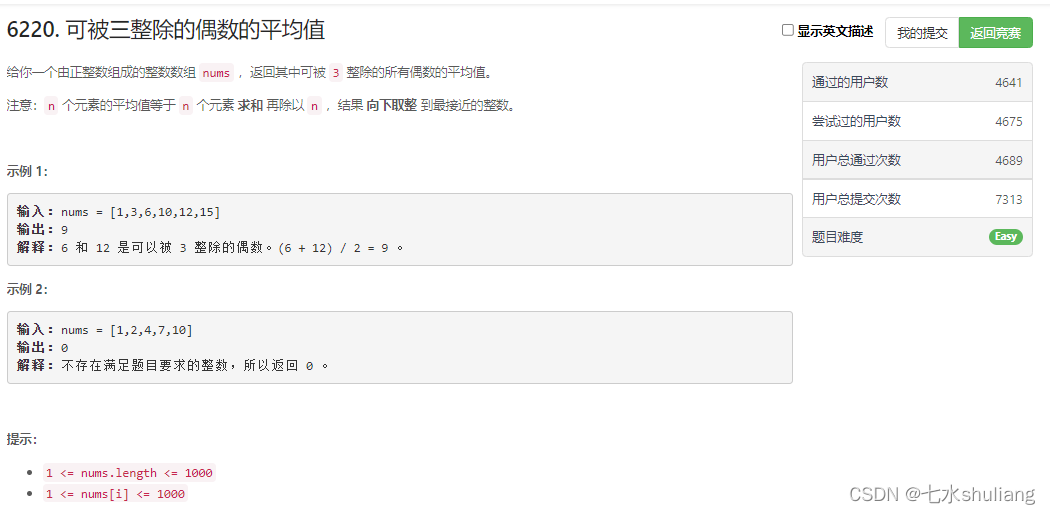
2. 思路分析
按题意模拟即可。
注意case2表示可以不存在,分母是0要特判
3. 代码实现
class Solution:
def averageValue(self, nums: List[int]) -> int:
s = 0
cnt = 0
for x in nums:
if x%6==0:
s +=x
cnt += 1
if cnt == 0:
return 0
return s//cnt
三、[Medium] 6221. 最流行的视频创作者
链接: 6221. 最流行的视频创作者
1. 题目描述
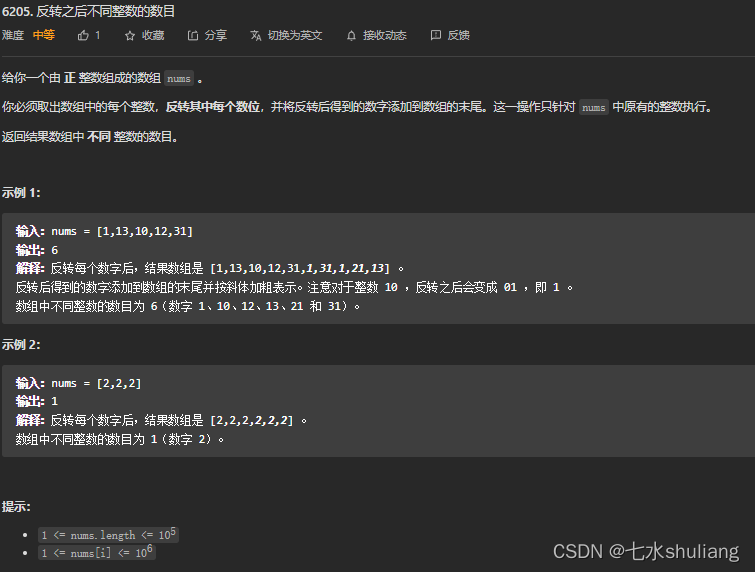
2. 思路分析
按题意模拟即可。
- s统计总播放量。
- p统计每个作者的所有视频以及播放量。
- 最后写个遍历统计最牛作者,这里就是如果遇到大的就替换ans;否则append
- 最后再处理作者,把他最大的视频找出来,我偷懒直接排序。
3. 代码实现
class Solution:
def mostPopularCreator(self, creators: List[str], ids: List[str], views: List[int]) -> List[List[str]]:
s = Counter()
p = defaultdict(list)
n = len(creators)
for c,i,v in zip(creators,ids,views):
s[c]+=v
p[c].append((-v,i))
mx = -1
ans = []
for k,v in s.items():
if v > mx:
mx = v
ans = [k]
elif v == mx:
ans.append(k)
ret = []
for c in ans:
i = sorted(p[c])[0][1]
ret.append([c,i])
return ret
四、[Medium] 6222. 美丽整数的最小增量
链接: 6222. 美丽整数的最小增量
1. 题目描述
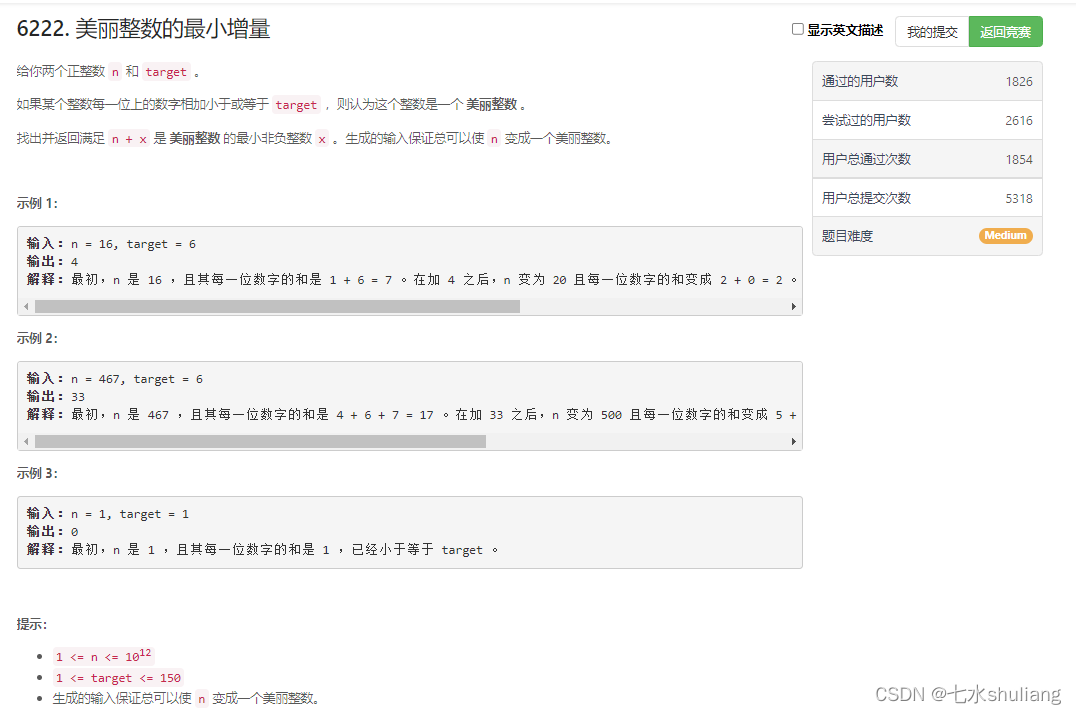
2. 思路分析
- 贪心。
- 我们发现要加上最小的数,那么首先会使低位变动,低位一定可以加上某个数变成全是0,然后进一位1.
- 因此我们从高位开始累加,直到和是最小的<=target-1的数,那么后续的低位就可以变0。
- 注意特判,如果最开始和就小于target,则答案是0。
3. 代码实现
class Solution:
def makeIntegerBeautiful(self, n: int, target: int) -> int:
s = str(n)
i = -1
p = 0
if sum(int(x) for x in s) <=target:
return 0
while i+1<len(s) and p + int(s[i+1])<= target - 1:
p += int(s[i+1])
i += 1
if i == len(s)-1:
return 0
# print(i)
r = int(s[i+1:])
ans = 10**(len(s)-i-1) - r
return ans
五、[Hard] 6223. 移除子树后的二叉树高度
链接: 6223. 移除子树后的二叉树高度
1. 题目描述
2. 思路分析
- 本题wa一次,RE一次,TLE一次。
- 第一次wa是思路错了,误以为考虑另一个孩子即可。实际应该考虑所有同层。0
- 第二次RE,因为没考虑同层只有一个孩子的情况,下标越界访问第二大了。
- 第三次TLE因为没删打印。。。。。
- 本题要求每次查询独立,还原初始状态。因此是快速查询删除某个子树后,整个树的树高。
- 我们发现,树的树高=高的那个子树=最深的节点。
- 删除一棵子树,如果这课子树在本层不是最高的,那么没影响,树高依然可以走最深那颗子树。
- 如果这棵树是本层最高的h0,那么应该走本层第二深的树h1,树总体减少的高度为h0-h1。
- 因此我们定义三个哈希表:
- dh:储存每个深度下所有子树和高度。(这里可以用小顶堆,因为只需要2个最大的元素)
- d:储存每个节点的深度,便于快速定位dh
- dd:储存每个节点的高度,便于快速计算答案。
- 通过dfs计算这三个哈希表,其中深度可以dfs传下去;高度则dfs后根遍历merge。
- 对于每一层,我们事先sort以便求最大和第二大。
- 特别的:如果本层只有一个节点,那么剪掉子树等于直接减去这一整颗子树的高度。
3. 代码实现
class Solution:
def treeQueries(self, root: Optional[TreeNode], queries: List[int]) -> List[int]:
dh = defaultdict(list) # 每个深度下,所有节点子树和他们的高度
d = {} # 每个节点的深度
dd = {} # 每个节点的高度
def dfs(root,depth):
if not root:
return 0
l = dfs(root.left,depth+1)
r = dfs(root.right,depth+1)
h = max(l,r)+1
dh[depth].append((h,root.val))
d[root.val] = depth
dd[root.val] = h
return h
h = dfs(root,0) # 树的总高
for k,v in dh.items():
v.sort(reverse=True)
ans = []
for q in queries:
vs = dh[d[q]] # 本层所有子树高
# print(vs)
if q == vs[0][1]:
# print(h,vs[0][0],dd[q])
if len(vs) == 1: # 本层只有一个节点,直接减去整颗子树的高度
ans.append(h-dd[q]-1)
else:
ans.append(h-(dd[q]-vs[1][0])-1) # 最深路径从第二高走,高度改变=最大值-第二大
else:
ans.append(h-1) # 不是最高的树高不变
return ans