1 理论基础
栈的底层实现可以是vector,deque,list 都是可以的, 主要就是数组和链表的底层实现。
我们常用的SGI STL,如果没有指定底层实现的话,默认是以deque为缺省情况下栈的底层结构。
栈不提供走访功能,也不提供迭代器(iterator)
std::stack<int, std::vector<int> > third; // 使用vector为底层容器的栈队列中先进先出的数据结构,同样不允许有遍历行为,不提供迭代器, SGI STL中队列一样是以deque为缺省情况下的底部结构。
std::queue<int, std::list<int>> third; // 定义以list为底层容器的队列2 力扣232.用栈实现队列
题目描述:
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
实现 MyQueue 类:
void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空,返回 true ;否则,返回 false
说明:
你 只能 使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
class MyQueue {
public:
stack<int> stIn;
stack<int> stOut;
/** Initialize your data structure here. */
MyQueue() {
}
void push(int x) {
stIn.push(x);
}
int pop() {
//相当于翻转栈
if (stOut.empty()) {
while (!stIn.empty()) {
stOut.push(stIn.top());
stIn.pop();
}
}
int result = stOut.top();
stOut.pop();
return result;
}
// 返回队列开头的元素
int peek() {
int res = this->pop();
stOut.push(res);
return res;
}
bool empty() {
return stIn.empty() && stOut.empty();
}
};
/**
* Your MyQueue object will be instantiated and called as such:
* MyQueue* obj = new MyQueue();
* obj->push(x);
* int param_2 = obj->pop();
* int param_3 = obj->peek();
* bool param_4 = obj->empty();
*/3 力扣225. 用队列实现栈
题目描述:
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
实现 MyStack 类:
void push(int x) 将元素 x 压入栈顶。
int pop() 移除并返回栈顶元素。
int top() 返回栈顶元素。
boolean empty() 如果栈是空的,返回 true ;否则,返回 false 。
注意:
你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
你所使用的语言也许不支持队列。 你可以使用 list (列表)或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
class MyStack {
public:
queue<int> que;
/** Initialize your data structure here. */
MyStack() {
}
/** Push element x onto stack. */
void push(int x) {
que.push(x);
}
//相当于左旋队列
int pop() {
int size = que.size();
size--;
while (size--) {
que.push(que.front());
que.pop();
}
int result = que.front();
que.pop();
return result;
}
/** Get the top element. */
int top() {
return que.back();
}
/** Returns whether the stack is empty. */
bool empty() {
return que.empty();
}
};
/**
* Your MyStack object will be instantiated and called as such:
* MyStack* obj = new MyStack();
* obj->push(x);
* int param_2 = obj->pop();
* int param_3 = obj->top();
* bool param_4 = obj->empty();
*/4 力扣20. 有效的括号
题目描述:
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。
class Solution {
public:
bool isValid(string s) {
if (s.size() % 2 != 0) return false;
stack<char>st;
char r;
for (int i = 0; i < s.size(); ++i) {
if (st.empty() && (s[i] == ')' || s[i] == ']' || s[i] == '}')) return false;
if (s[i] == '(' || s[i] == '[' || s[i] == '{') st.push(s[i]);
else if (s[i] == ')') {
if (st.top() != '(') return false;
else st.pop();
}
else if (s[i] == ']') {
if (st.top() != '[') return false;
else st.pop();
}
else if (s[i] == '}') {
if (st.top() != '{') return false;
else st.pop();
}
}
return st.empty();
}
};5 力扣150. 逆波兰表达式求值
题目描述:
给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
注意:
有效的算符为 '+'、'-'、'*' 和 '/' 。
每个操作数(运算对象)都可以是一个整数或者另一个表达式。
两个整数之间的乘法总是 向零截断 。
表达式中不含除零运算。
输入是一个根据逆波兰表示法表示的算术表达式。
答案及所有中间计算结果可以用 32 位 整数表示。
适合用栈操作运算:遇到数字则入栈;遇到算符则取出栈顶两个数字进行计算,并将结果压入栈中
class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<int> st;
for (int i = 0; i < tokens.size(); i++) {
if (tokens[i] == "+" || tokens[i] == "-" || tokens[i] == "*" || tokens[i] == "/") {
int num1 = st.top();
st.pop();
int num2 = st.top();
st.pop();
if (tokens[i] == "+") st.push(num2 + num1);
if (tokens[i] == "-") st.push(num2 - num1);
if (tokens[i] == "*") st.push(num2 * num1);
if (tokens[i] == "/") st.push(num2 / num1);
} else {
st.push(stoi(tokens[i]));
}
}
int result = st.top();
st.pop();
return result;
}
};逆波兰表达式:
逆波兰表达式是一种后缀表达式,所谓后缀就是指算符写在后面。
平常使用的算式则是一种中缀表达式,如 ( 1 + 2 ) * ( 3 + 4 ) 。
该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。
逆波兰表达式主要有以下两个优点:
去掉括号后表达式无歧义,上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
6 力扣239. 滑动窗口最大值
题目描述:
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
7 力扣347.前 K 个高频元素
题目描述:
给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
8.力扣42.接雨水
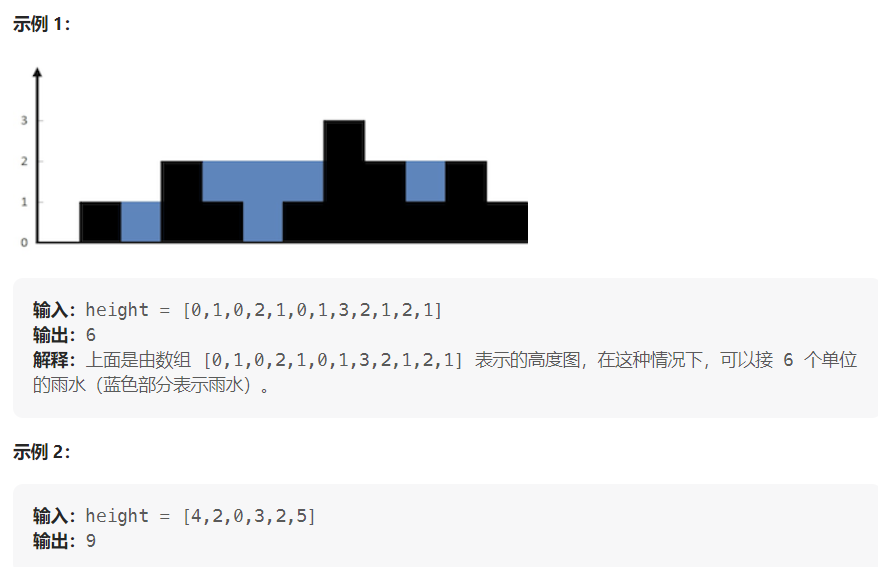
题目描述:
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
9 力扣1047. 删除字符串中的所有相邻重复项
题目描述:
给出由小写字母组成的字符串 S,重复项删除操作会选择两个相邻且相同的字母,并删除它们。
在 S 上反复执行重复项删除操作,直到无法继续删除。
在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。
class Solution {
public:
string removeDuplicates(string S) {
string result;
for(char s : S) {
if(result.empty() || result.back() != s) {
result.push_back(s);
}
else result.pop_back();
}
return result;
}
};