1. 集群分片算法

1.1 集群概述

首先对于"集群"这个概念是存在不同理解的：

• 广义的"集群"：表示由多台主机构成的分布式系统，称为"集群"
• 狭义的"集群"：指的是redis提供的一种集群模式，用来解决存储空间不足的问题（拓展存储空间）

前面我们介绍的哨兵、主从模式都是为了保障系统的可用性，但是目前为止，无论是主节点还是从节点都需要完整的保存数据的全集，但是当前是一个"大数据时代"，我们希望能够保证高效的同时，存储空间足够，因此引入了"集群模式"

1.2 分片算法

那么我们如何将数据分成多份，保存在不同的节点中呢？此时的每一份数据被称为一个"分片"（sharding）
常见的分片算法有如下三种：

1. 哈希求余算法
2. 一致性哈希算法
3. 哈希槽分区算法

1.2.1 哈希求余算法

该算法本质借鉴了哈希表这种数据结构的思想：借助哈希函数将一个key映射为一个整数，然后对数组的长度进行取余操作得到对应数组下标，即保存位置。同理，哈希求余算法也是一样，比如一共分为三个分片，标记为0，1，2。然后就将redis中的key使用一种哈希算法（比如md5）计算结果得到hash值，然后对分片总数3进行取余操作得到对应的分片下标

示例：假设hash(key) % 3 == 0 => 计算得出保存的分片编号为0，于是将数据保存在0号分片上；当需要获取数据的时候也是通过同样的key以及同样的hash算法，经过计算hash(key) % 3 ==0 得到分片位置，取出数据

值得一提的是md5算法就是常见的哈希算法，内部经过一系列的数学运算能够将一个字符串转换为整数值，其特点如下：

1. md5的计算结果是定长的，比如使用md5-16算法，无论原始字符串是怎样的，最终的计算结果都是一个16位的16进制数字
2. md5计算结果是分散的，意味着即使两个输入字符串大部分内容相同，只有少部分不同，得到的计算结果也是大相径庭的
3. md5是不可逆的（也用于加密算法），表示给定一个输入字符串可以轻易计算出结果，但是给定结果却无法还原出输入内容

哈希求余缺点：
当前哈希求余算法存在一定的缺点，比如当前为3个分片，哈希函数为hash(key) = key，再对3取余得到当前的分片结果为：0：102，105，108，1：103，106，109，2：104，107，110，但是此时需要进行扩容：重新哈希后分片结果为：0：104：108，1：105，109，2：102，106，110，3：103，107，不难发现，扩容之后大部分数据都需要进行迁移搬运。
总结：
因此当前扩容过程开销是很大的，是万万不能在生产环境上执行的，只能通过"替换"等曲线救国方式来实现扩容，成本更高、操作步骤也更为复杂了。

1.2.2 一致性哈希算法

为了降低上述的搬运开销，业界又提出了"一致性哈希算法"，从key映射到分片序号的过程就不再是简单求余了，而是改成了以下过程：
Step1：将0 - 2^32 - 1这个数据空间，映射到一个圆环上，数据按照顺时针方向增长

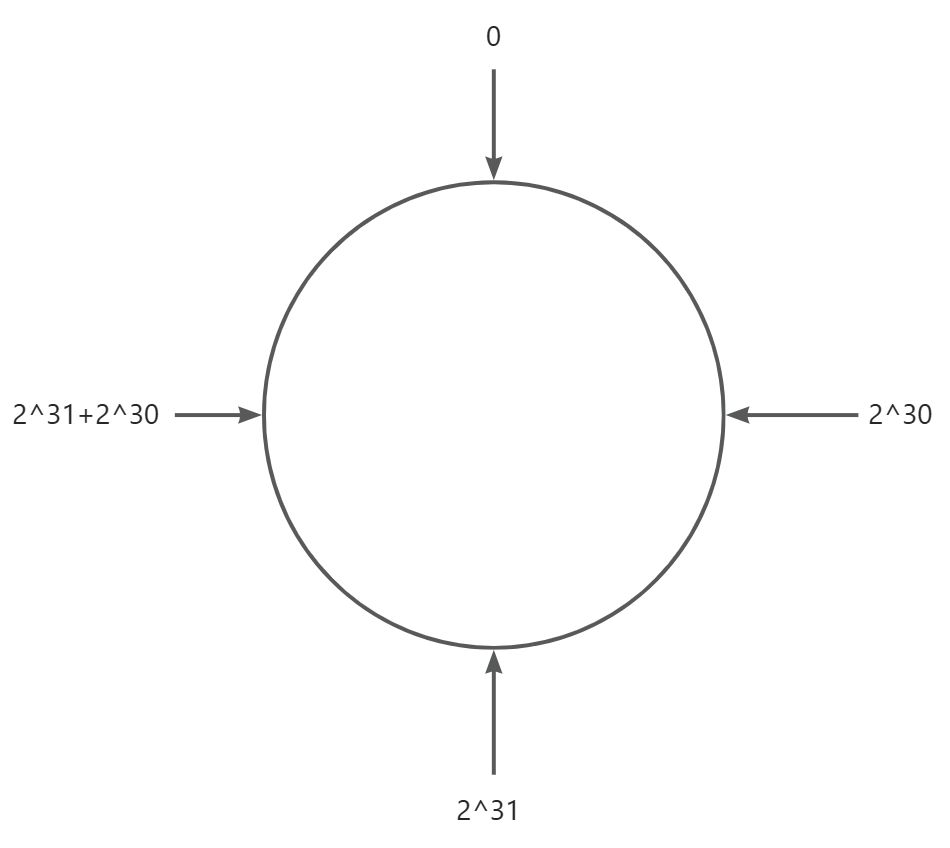
Step2：假设当前存在3个分片，就把分片指针放到对应的位置：

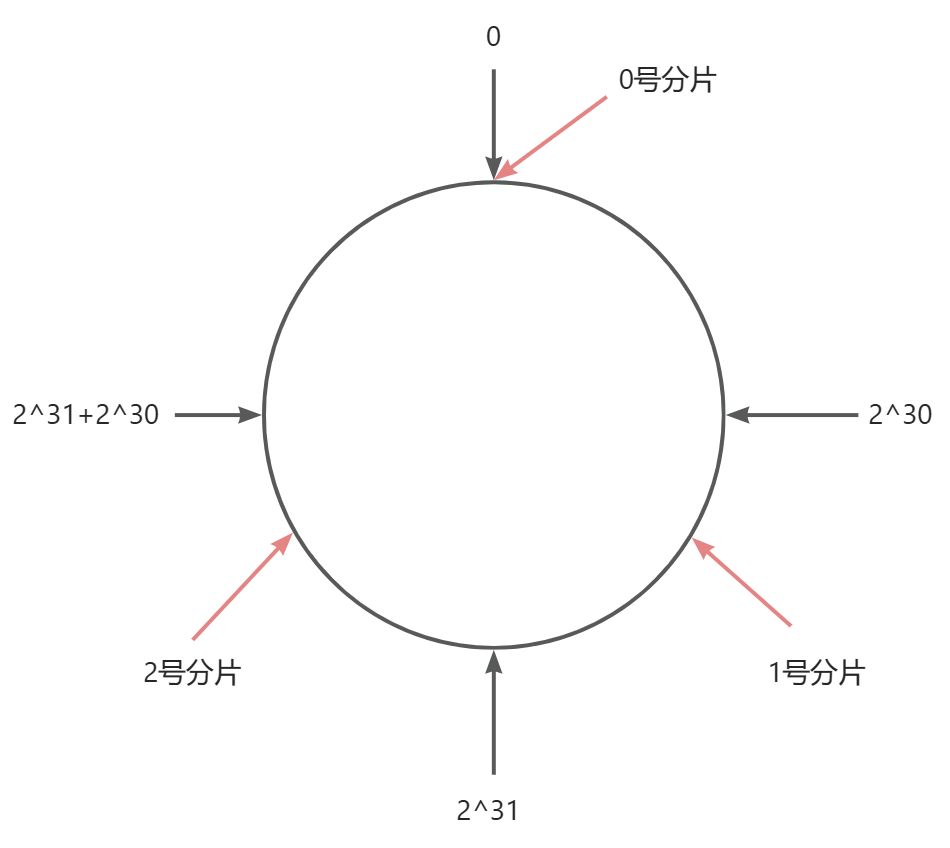
Step3：假设有一个key，计算得到hash值为H，那么应该分配到哪个分片上呢？规则很简单，就是找到对应的位置然后顺时针找到的第一个分片就是其从属的分片位置

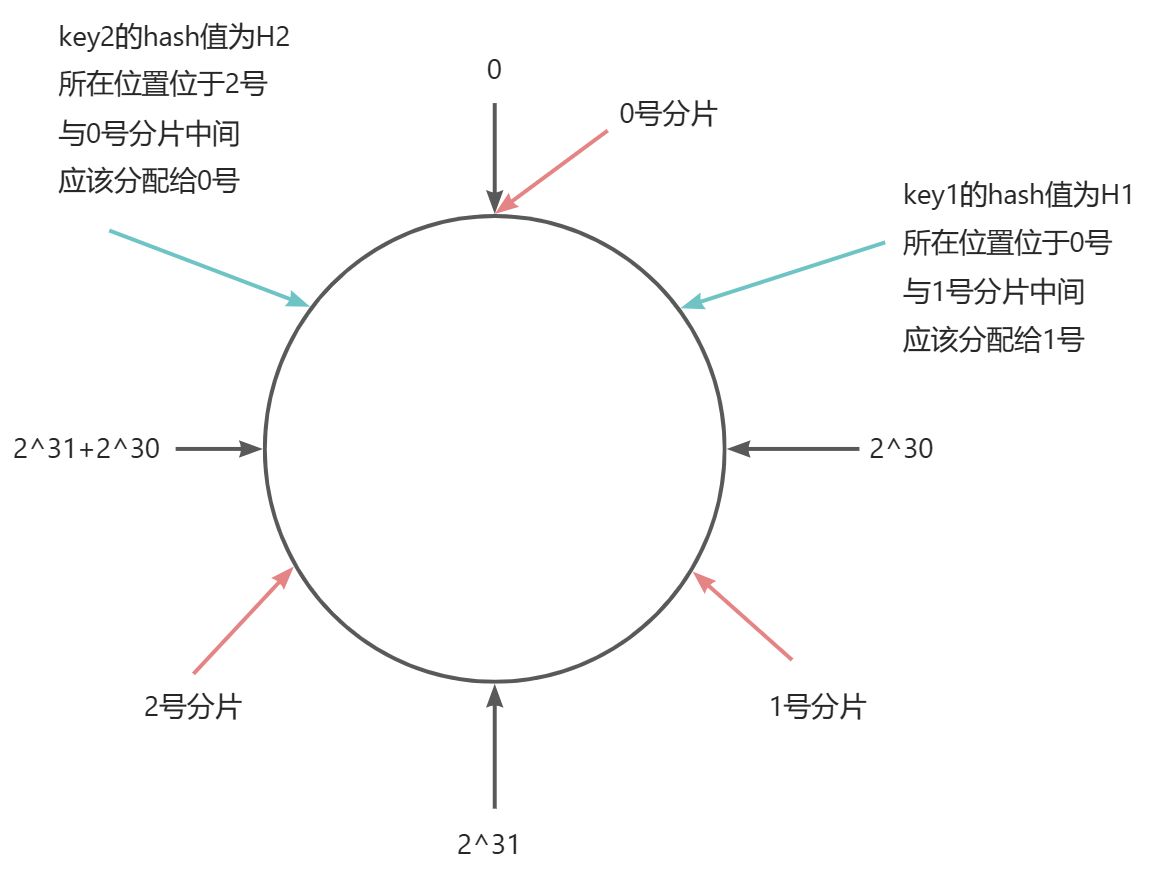
Step4：如果此时需要扩容，分片数由3 -> 4应该如何操作呢？、

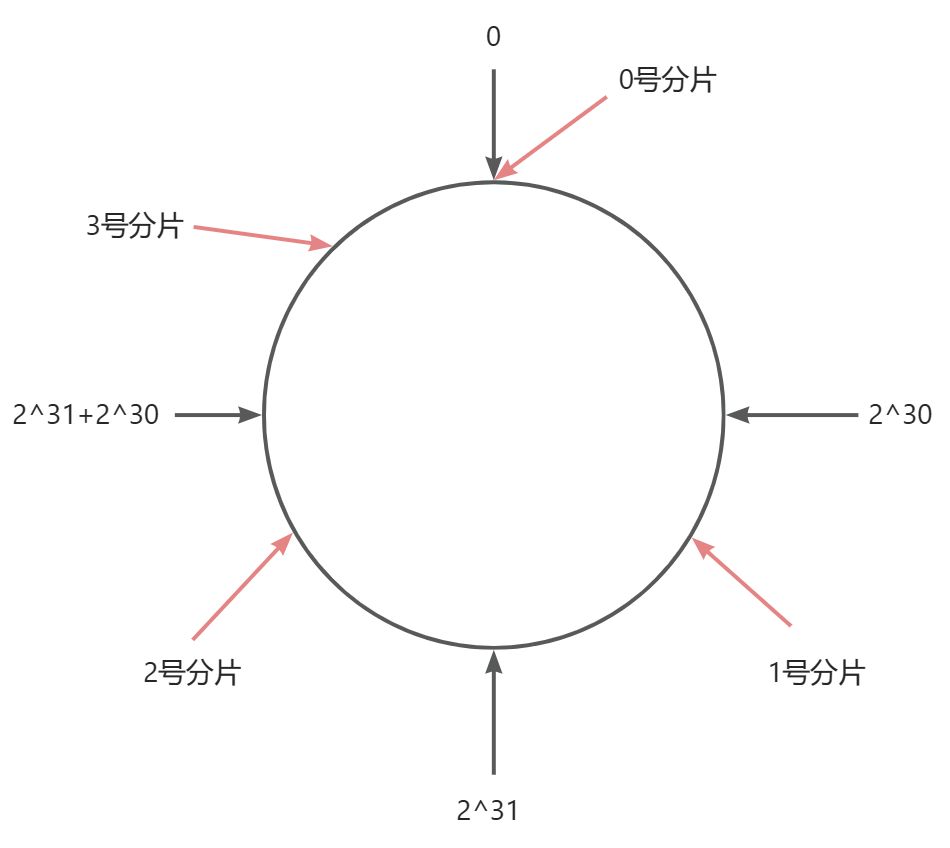
我们随机在圆盘上找一个位置插入3号分片，此时只需要将2号分片的部分数据搬运到3号分片上就完成了搬运操作，上述过程虽然仍存在一定的搬运开销，但是相比较于哈希求余算法，就要少的多了，但是一致性哈希算法也存在着一个重要缺点：
一致性哈希缺点：
那就是存在"数据倾斜"问题，当前如果平均将0-2^32-1数据空间划分为0，1，2三个分片，一旦进行扩容，就会导致每个分片的数据量不均衡

1.2.3 哈希槽分区算法

这是redis真正采取的算法，其哈希槽计算公式为hash_slot = crc16(key) % 16384
该种算法实质上是将哈希求余算法和一致性哈希算法结合了起来，下面给出了一种分配方式
假设当前有三个分片：

• 0号分片：[0, 5641]共5642个槽位号
• 1号分片：[5642，10923]共5642个槽位号
• 2号分片：[10924，16383]共5460个槽位号

虽然不是严格意义上的平均分配，但是差异非常小，可以近似看做是均匀分配了，并且每个分片还会使用位图这样的数据结构表示当前具有槽位号，16384个比特位 => 2KB存储空间

注意：这里只是其中一种分配方式，事实上分配方式是非常灵活的，每个分片持有的槽位号可以是连续的，也可以是不连续的

问题一：Redis集群是最多有16384个分片么？
如果redis集群有16384个分片，此时按照平均划分每个分片分配到一个槽位号（很难），因为我们的key是先映射到槽位号，然后再映射到分片上的，此时就很难保证各个分片的均衡性。
实际上redis的作者建议集群分片数不应该超过1000
问题二：为什么是16384个槽位号？
这个问题有人在github上询问了，作者给出的答复是：由于我们redis集群节点之间后续需要通过频繁传递心跳包检测是否存活，而心跳包中包含了某个分片含有哪些槽位号等信息，16384个槽位号可以用2KB存储，但是65535就需要8KB了，16384能保证通信可用性的同时尽可能节省网络带宽等资源

2. 集群故障恢复

集群故障：如果当前集群中有节点挂了，应该怎么办？这里需要分情况讨论：

• case1：如果挂了的是从节点，那就没事
• case2：如果挂了的是主节点，那就需要进行故障转移操作

2.1 故障判定

该步骤主要用于确定集群中哪个节点挂了，主要流程如下：

1. 节点之间通过心跳包进行通信：比如节点A给节点B发送ping包，节点B需要给节点A返回pong包（这两个数据包只有message type字段不同，其余内容相同）心跳包中包含集群的配置信息，比如节点id、节点从属于哪个分片、是主节点还是从节点、持有哪些slots的位图
2. 每个节点每秒钟都会给随机一些节点发送ping包，不是全发一遍（避免节点很多时洪泛发送心跳包）
3. 当节点A给节点B发送ping包，B不能如期回应时，A就会尝试重置和B的TCP连接，如果仍连接失败，就会把B标记为PFAIL状态（主观下线）
4. A判定B为PFAIL之后，就会通过redis内部Gossip协议与其他节点通信，确认B的状态（每个节点会维护一个主观下线列表）
5. 如果超过半数节点认为B主观下线，那么A就会把B标记为FAIL状态（客观下线），并将此消息同步给其他节点

2.2 故障迁移

该步骤主要用于保障集群可用性，假设节点B被标记为FAIL客观下线，存在两种情况：

• 如果是主节点，则将由B的从节点来触发故障转移
• 如果是从节点，则不会触发故障转移操作

故障转移流程：

1. 从节点判定自身是否有资格参与选举，如果主从之间太久没有通信，时间超过阈值，则没有资格参与选举
2. 具有资格的从节点比如C和D，就会休眠上一段时间（500ms基础时间 + [0，500]ms随机时间 + 排名 * 1000ms），其中offset同步值越大，排名靠前（越小）
3. 比如C的休眠时间到了，C就会给集群中其他节点发送请求，申请拉票（只有主节点才有资格投票）
4. 当节点C的得票数超过半数主节点之后，C就会晋升成为主节点（自己执行slaveof no one）并让D执行slaveof C
5. 同时C还会把自己晋升为主节点的事，同步给集群中其余节点，大家就会更新保存的集群结构信息