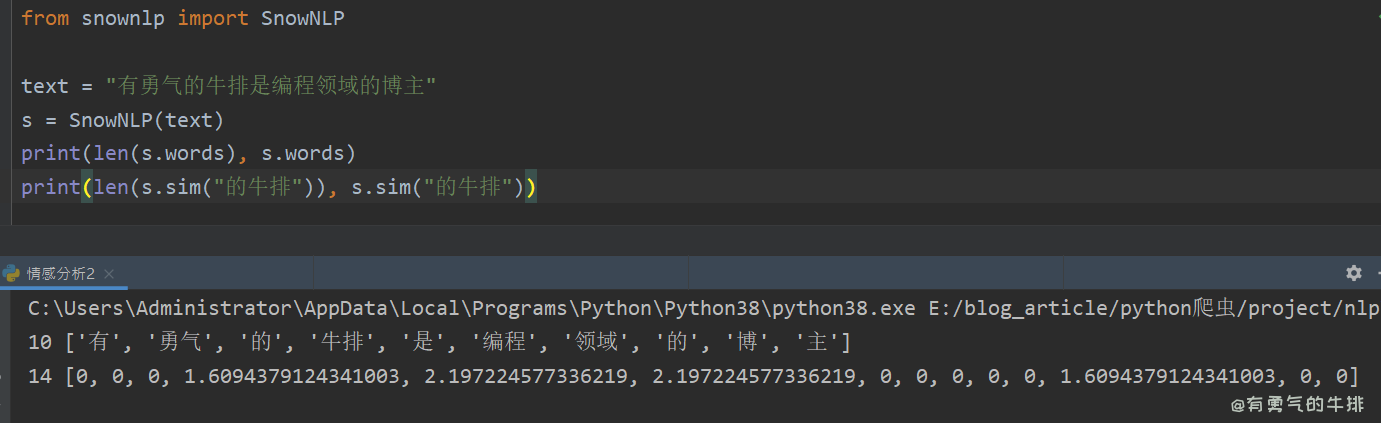
1. 前言

快慢双指针是一种常用的算法技巧，通常用于解决涉及链表或数组的问题。它的基本思想是使用两个指针，一个移动速度快（快指针），一个移动速度慢（慢指针），来解决特定的问题。这两个指针通常从序列的起始位置开始，并以不同的步伐向前移动，直到达到特定的条件为止。

• 快慢双指针是指在算法处理过程中，使用两个指针，分别从序列的起始位置出发，按照不同的步伐向前移动，直到满足某种条件。通常快指针的移动速度比慢指针快，这样可以加快算法的执行速度。

• 判断链表是否有环：快指针每次移动两步，慢指针每次移动一步，如果存在环，快指针最终会追上慢指针。

• 找到链表的中间节点：快指针每次移动两步，慢指针每次移动一步，当快指针到达链表末尾时，慢指针所在位置即为中间节点。

• 移除排序数组中的重复项：使用快慢指针，当快指针遇到不同的元素时，将其复制到慢指针位置，然后慢指针前进一步。

 2. 我对快慢指针的理解

1. 数组划分

1. cur：从左到右扫描数组，遍历数组(快指针)
2. dest：已处理的区间内，非零元素的最后一个位置
3. cur(快指针)遇到符合题意的值，把他加入这个区间。一般是先dest++然后和cur交换

如何做到维护该区间一直到结束，是解题的关键。

// 符合题意           不符合题意            未处理元素
// [0~dest]        [dest + 1 ~ cur]       [cur + 1 ~ n]

达到最终的目的就是持续这三块区域的关系

2. 判断是否成环

快指针每次移动两步，慢指针每次移动一步，如果存在环，快指针最终会追上慢指针。

3 例题分析

3.1 移动零 (数组划分)

 

public void moveZeroes(int[] nums) {
        // 符合题意(非0元素)    不符合题意(0)    未处理元素
        // [0~dest]        [dest + 1 ~ cur]       [cur + 1 ~ n]
        // 要想维护上面的关系到结束，必须让cur遇到符合题意的和dest后一个元素(不符合题意的交换)，
        //                        然后让dest++(扩大符合题意的范围)，继续维护该区间
        int n = nums.length, cur = 0, dest = -1;
        while(cur != n){
            if (nums[cur] != 0){//遇到符合题意的，交换来维持三个区间关系
                dest++;
                int temp = nums[dest];
                nums[dest] = nums[cur];
                nums[cur] = temp;
            }
            cur++;
        }
    }

3.2 去重

下面的图，就是我对上题一步步的分析：

只要一直维持这三个区域到结束，就可以解答本题。

如何维持，就成了解答本题的关键。

    /**
     * 思路分析：
     * 1. dest(慢指针)：确定没有重复元素的最后一个位置， cur(快指针)：扫描完的最后一个位置
     * 2. 通过比较快慢指针的内容确定是否重复 (因为非严格递增，相同的都是连续的)
     * 3. 遇到一个不重复元素，就是符合[0 ~ dest]区间，就和dest+1不符合该区间的交换位置
     *
     * @param arr
     * @return
     */
    public static int[] arrayDeduplication(int[] arr) {
        //默认第一个元素不重复
        int n = arr.length, dest = 0, cur = 1;
        while (cur < n) {
            if (arr[cur] != arr[dest]) {//找到一个不符合题意的
                dest++;
                int temp = arr[dest];
                arr[dest] = arr[cur];
                arr[cur] = temp;
            }
            cur++;
        }
        return Arrays.copyOf(arr,dest + 1);
    }

    public static void main(String[] args) {
        int[] arr = {1, 1, 4, 4, 5, 6, 7, 7, 8, 8, 8, 8, 8};
        int[] distinction = arrayDeduplication(arr);
        System.out.println(Arrays.toString(distinction));
        System.out.println(Arrays.toString(arr));
    }

3.3 复写零

思路分析：

因为正序会造成覆盖，比如 0 1 2  正序读0索引->会变成 0 0 1，下次读1索引就被覆盖了。 

1. 先判断要舍弃的元素。(因为要复写，数组大小不变总要舍去)
2. 从后往前复写，0写两次，其余写一次
3. 判断临界情况，防止最后一个为0且数组长度不够

剩下的内容代码有详细的注释。 

  // 正着写会被覆盖，因此倒序，倒序要确定复写舍弃的元素(复写位置)，最后处理临界：cur越界
    // 1. 通过 0 cur移动两步 和 非0 cur移动一步，确定从dest位置开始复写
    // 2. 倒序开始写，dest读取到0复写 cur写两遍  非0  cur写一遍
    // 3. 处理临界：最后一个修改成0， dest-2  cur-1
    public static void duplicateZeros(int[] arr) {
        //因为读完写，所以dest(慢指针)为0，cur为-1
        int n = arr.length, dest = 0, cur = -1;
        //1.确定dest位置
        while(dest < n){
            if (arr[dest] == 0){//写两边
                cur++;cur++;
            }else {//写一遍
                cur++;
            }
            if (cur >= n - 1) break;//写到最后或者写过(最后一个为0)，dest就不需要读了
            dest++;
        }
        //3. 处理临界
        if (cur == n){
            arr[n - 1] = 0;
            cur--;cur--;
            dest--;
        }
        //此时dest后面就是舍弃的元素
        //2. 倒序复写
        while(dest >= 0){
            if (arr[dest] == 0){//写两边
                arr[cur--] = 0;
                arr[cur--] = 0;
            }else {//写一遍
                arr[cur--] = arr[dest];
            }
            dest--;
        }
    }

 

3.4 快乐数（判断环）

 通过数字的取平方和来模拟移动，取一次移动一步，俩次移动两步，这样就可以模拟链表。和判断链表是否有环，原理一样，仅需判断链表中元素是否为1即可。

为什么是必定有环的呢？？？

原因就是鸽巢原理，所以数据范围有限的情况下，必定有环。5个人有6个糖，必定有一个人是有两个糖即以上的。

public class Test3 {
    //通过数来模拟指针移动，和判断链表是否有环，原理一样
    //仅需判断链表中元素是否为1即可
    //要么是1，要么无限循环的原因就是鸽巢原理，所以数据范围有限的情况下，必定有环
    public boolean isHappy(int n) {
        int slow = n, fast = bitSum(n);
        while(slow != fast){
            slow = bitSum(slow);
            fast = bitSum(bitSum(fast));
        }
        return slow == 1;
    }

    //求一个数各个元素的平方和，相当于移动一次
    private int bitSum(int num){
        int sum = 0;
        while(num != 0){
            int t = num % 10;
            sum += t * t;
            num /= 10;
        }
        return sum;
    }
}