文章目录
- 1. 经验误差与过拟合
- 2. 模型评估方法
- 2.1 模型评估概念
- 2.2 留出法
- 2.3 k 折交叉验证法
- 2.4 自助法
- 2.5 调参与最终模型
- 3. 性能度量
- 3.1 均方误差
- 3.2 错误率、精度
- 3.3 查准率、查全率
- 3.3 扩展
- 3.4 ROC 与 AUC
- 3.5 代价敏感错误率与代价曲线
- 4. 比较检验
- 4.1 假设检验
- 4.2 交叉验证 t 检验
- 4.3 McNemar 检验
- 4.4 Friedman检验 与 Nemenyi后续检验
- 5. 偏差与方差
前言:
本文为个人学习笔记
灰色部分且标注为思考的 为个人理解部分,可能会有错误的地方
黑色部分为文章原文笔记。
1. 经验误差与过拟合
错误率:分类错误的样本占样本总数的比例。例:m 个样本中有 a 个样本分类错误,错误率
E
=
a
m
E = \frac{a}{m}
E=ma
精度:
1
−
a
m
1 - \frac{a}{m}
1−ma
误差:实际预测输出与样本真实输出的差异
训练误差:在训练集上的误差
泛化误差:在新样本上的误差
分类错误率为 0,分类精度为 100% 会导致
过拟合,导致泛化能力下降。与之相对的是欠拟合。过拟合无法避免,只能 ‘缓解’
模型选择:对候选模型的泛化误差进行评估,选择泛化误差最小的模型,减小过拟合现象
2. 模型评估方法
2.1 模型评估概念
选择 测试集 测试学习器对新样本的差别能力,以测试集上的 测试误差 作为 泛化误差 的近似值。通常 测试样本 也是从样本真实分布中 独立同分布采样 得到,测试集应该尽可能 与训练集互斥,即测试集在训练集中尽量未出现、未在训练过程中使用过。
以下是几种模型评估做法
2.2 留出法
将数据集 D 划分为两个互斥的集合 S 和 T。S 作为训练集,T 作为测试集。即
D
=
S
⋃
T
,
S
⋂
T
=
∅
D = S \bigcup T,S \bigcap T = \varnothing
D=S⋃T,S⋂T=∅
在 S 上训练出模型后,用 T 来评估误差,作为泛化误差的估计

S 和 T 要尽可能保持数据分布的一致性。保留类别比例的采样方式称为
分层采样。例如 D 中包含 500 个正例 500 个反例,则 S 应包含 350个正例350个反例,T 中应包含 150个正例150个反例。若 S 、T 中样本类别比例差异很大,则误差估计会因为数据分布差异导致偏差。
S 和 T 中数据分布可能导致模型评估的结果有差别。单次使用留出法得到的估计结果往往不够稳定和可靠。使用留出法时,一般用若干次随机划分、重复进行实验评估后取平均值作为留出法的评估结果。例如进行 100 次随机划分,得到100个结果后取平均值
留出法还会导致一个问题:
若令训练集 S 包含大多数样本,则训练的模型可能更接近 D 训练的模型。但由于 T 较小,评估结果可能不够稳定准确;若令 T 包含更多一些的样本,则 S 训练的模型与 D 训练的模型差异会稍大一些,评估结果与 D 的结果会有更大的差别,从而降低评估真实性。这个问题没有完美解决方案,常见做法是将大约 2/3 ~ 4/5 的样本用于训练,剩余样本用于测试。
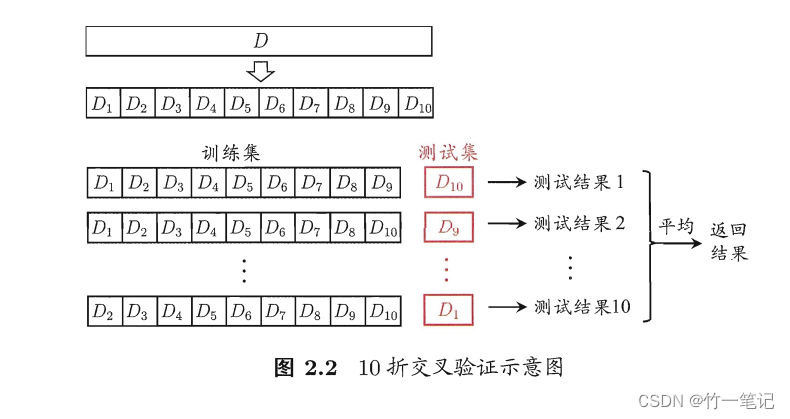
2.3 k 折交叉验证法
将数据集 D 划分为 k 个大小相似的互斥子集,即
D
=
D
1
⋃
D
2
⋃
.
.
.
⋃
D
k
,
D
i
⋂
D
j
=
∅
(
i
≠
j
)
D = D_1 \bigcup D_2 \bigcup ... \bigcup D_k, D_i \bigcap D_j = \varnothing(i \not = j)
D=D1⋃D2⋃...⋃Dk,Di⋂Dj=∅(i=j)
每个子集尽可能保持数据分布的一致性,即从 D 中通过分层采样得到。每次用 k - 1 个子集用于训练,余下子集作为测试集,从而进行 k 次训练和测试,最终得到 k 个结果的均值作为泛化误差近似。
交叉验证法评估结果很大程度上取决于 k 的取值。k 常用取值是 10,此时称为
10折交叉验证
与留出法相同,k 个子集同样存在不同的划分方式。为了减小样本划分差异导致的差别,通常需要将数据集划分 p 次,最终评估 p 次 k 折交叉验证结果的均值。例如:
10次10折交叉验证
留一法:若 D 中包含 m 个样本,令 k = m,则留一法不受随机样本划分方式的影响,评估结果最准确。但是开销太大了,假设有 100 万样本,不考虑参数影响情况下,要训练100万次
2.4 自助法
自助法 解决了 交叉验证和留出法的 S 小于 D 导致评估结果产生偏差的问题。
给定 m 个样本的数据集 D,对它采样产生数据集 D’:每次随机从 D 中复制一个到 D’,重复 m 次,复制过的样本还可能被重新复制到 D’ 中。显然,有一部分样本会在 D’ 中重复出现,另一部分样本不会出现。
样本在 m 次采样中始终不被采到的概率是
(
1
−
1
m
)
m
(1 - \frac{1}{m})^m
(1−m1)m
lim
m
−
>
∞
(
1
−
1
m
)
m
⟹
1
e
≈
0.368
\lim\limits_{m->∞}{(1 - \frac{1}{m})^m} \implies \frac{1}{e} \approx 0.368
m−>∞lim(1−m1)m⟹e1≈0.368
即通过自助采样,初始数据集中约有 36.8% 的样本未出现在采样数据集 D’ 中,于是我们可以用 D’ 当作训练集,D - D’ 当作测试集。
自助法在数据量较小,难以有效划分测试集、训练集时很有用。但是,自助法产生的数据集改变了初始数据集的数据分布,会引入估计偏差。因此在数据量足够时,用留出法和交叉验证法更常用
2.5 调参与最终模型
大多数学习算法都有参数设定,因此除了对学习算法进行选择,还要对算法参数进行评定,即 调参

测试集 T:用来评估泛化能力
验证集 V:调参
D = S + T + V
数据量小时,可以不区分 T 和 V
3. 性能度量
性能度量:衡量模型泛化能力的评价标准。不同的性能度量会导致不同的评判结果,模型的好坏是相对的
3.1 均方误差
回归 任务常用的性能度量是 均方误差

3.2 错误率、精度
分类 任务常用 错误率 和 精度

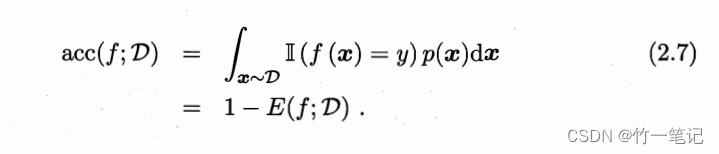
3.3 查准率、查全率
例如二分类问题,可分为
- 真正例:TP
- 假正例:FP
- 真反例:TN
- 假反例:FN
显然
T P + F P + T N + F N = 样例总数 TP + FP + TN + FN = 样例总数 TP+FP+TN+FN=样例总数
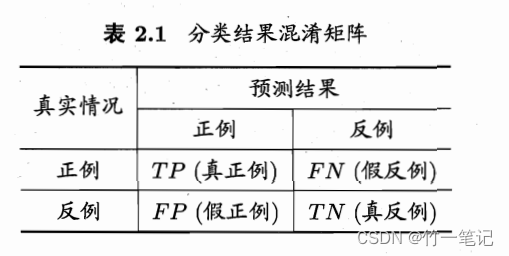
查准率 : p = T P T P + F P 查全率: R = T P T P + F N 查准率: p = \frac{TP}{TP+FP}\\ 查全率:R = \frac{TP}{TP+FN} 查准率:p=TP+FPTP查全率:R=TP+FNTP
查准率:模型检测为正中,真正的比例
查全率:所有正例中,模型检测出来的比例
PR曲线
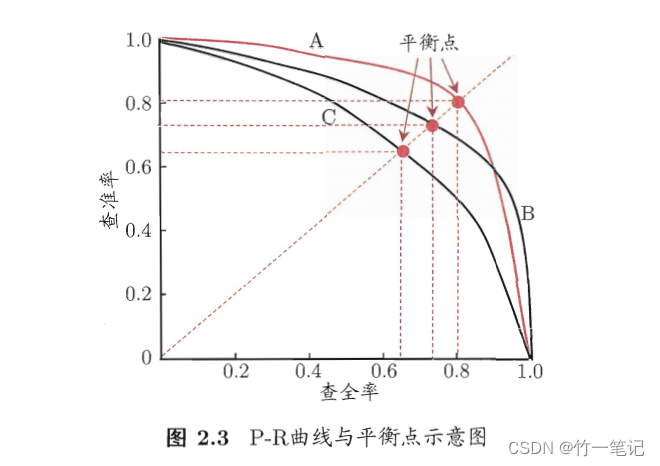
PR曲线,同一个模型不同训练参数,或不同模型,对应一条曲线。
思考
PR曲线为什么画出来是一条线?同一个模型相同参数训练结果的查全率和查准率难道不是一个值吗?
因为 pr 曲线是通过修改阈值得到的。例如二分类问题,模型给出的结果是0-1之间的数。假设大于0.5是好瓜,会得到1个点,大于0.6是好瓜,又得到一个点。通过修改不同的阈值表示正,可以得到 pr 曲线
- 查准率和查全率曲线越靠
右上,说明模型越好,即曲线包住别的曲线- 如果2个曲线有交叉点,则根据PR曲线下面积大小判断模型好坏
- 根据
平衡点 BEP度量,查找查准率 = 查全率的取值。图中 A 优于 B 优于 CF1度量优于 BEP 度量
F 1 = 2 ∗ P ∗ R P + R = 2 ∗ T P 样例总数 − T P − T N F1 = \frac{2 * P * R}{P + R} = \frac{2 * TP }{样例总数 - TP - TN} F1=P+R2∗P∗R=样例总数−TP−TN2∗TP
不同模型对查准率和查全率有不同偏好,F1度量的一般形式
F β = ( 1 + β 2 ) ∗ P ∗ R ( β 2 ∗ P ) + R , β { < 1 倾向于查准率 , = 1 退化为F1 > 1 倾向于查全率 F_\beta = \frac{(1+\beta^2)*P*R}{(\beta^2*P)+R},\beta\begin{cases}<1&\text{倾向于查准率},\\=1&\text{退化为F1}\\>1&\text{倾向于查全率}\end{cases} Fβ=(β2∗P)+R(1+β2)∗P∗R,β⎩ ⎨ ⎧<1=1>1倾向于查准率,退化为F1倾向于查全率
3.3 扩展
用来衡量机器学习算法的能力指标
宏查准率:macro-P
宏查全率:macro-R
宏F1:macro-F1
微查准率:micro-P
微查全率:micro-R
微F1:micro-F1


思考
宏和微举个例子,假如你生病了,有100个药和10个玩具,你要的是药
- 药多,玩具多,药重要,就用微(数量多)
假如你生病了,有10个药和100个玩具,你要的是药
- 药少,玩具多,药重要,就用宏(数量不占上风)
用宏还是用微,先看更关注哪个,再看数量。
就好像跟女朋友吵架的时候,女朋友吵架,她占理她就讲对错,她不占理她就讲态度。。。。
3.4 ROC 与 AUC
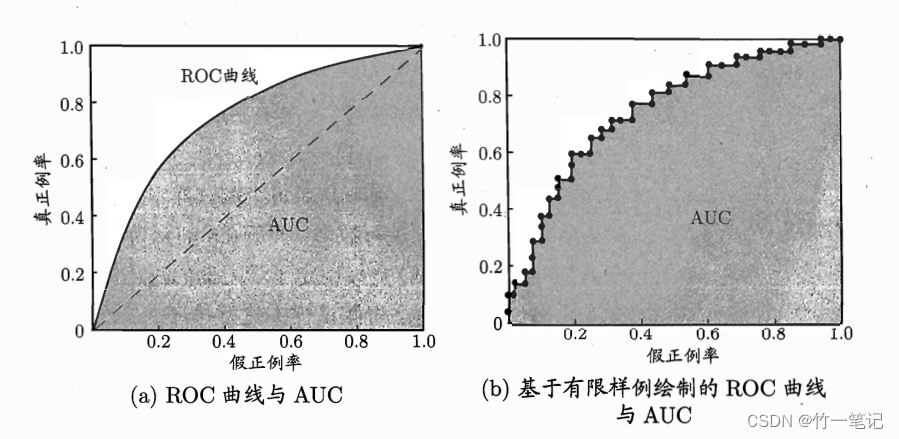
ROC:受试者工作特征(Receiver Operating Characteristic)曲线。训练模型后,根据学习器的预测结果对样例进行排序,按此顺序逐个把样本作为正例预测,以假正例率 FPR 为横轴,真正例率 TPR 为纵轴。每个正反例截断点在坐标轴上得到一个点,改变截断点的值,得到一条曲线,即为ROC曲线
T
P
R
=
T
P
T
P
+
F
N
F
P
R
=
F
P
T
N
+
F
P
TPR = \frac{TP}{TP+FN}\\FPR = \frac{FP}{TN+FP}
TPR=TP+FNTPFPR=TN+FPFP
思考
考虑极端情况,假定截断点为 1,没有正例被识别为正例,真正例 TP = 0,根据公式得 真正例率 TPR = 0;同理 没有反例被识别为正例,FP = 0,FPR = 0。对应图上(0,0)点
假定截断点为 0,所有正例都被识别为正例,即没有正例被识别为反例,所以 FN = 0,也没有反例被识别为反例,反以 TN = 0。对应图上(1,1)点
T P R = T P T P + F N = T P T P = 1 F P R = F P T N + F P = F P F P = 1 TPR = \frac{TP}{TP+FN} = \frac{TP}{TP} = 1\\ FPR = \frac{FP}{TN+FP} = \frac{FP}{FP} = 1 TPR=TP+FNTP=TPTP=1FPR=TN+FPFP=FPFP=1
而图中的(0,1)点,假正例率 = 0,真正例率 = 1。所有正例被正确识别。FPR = 0,TPR = 1,由公式可看出,FN = 0,所以也没有反例被识别为正例,因此,(0,1)点为 roc 曲线的理想点,把所有正例排在反例之前,且正确找到截断点,是一个理想模型
ROC曲线 与 P-R曲线 相似,若一个学习器的 ROC 曲线 a 被 另一个ROC 曲线 b 包住,则 b 的性能优于 a 的性能。若两个曲线发生交叉,则比较 ROC 曲线的下面积大小,称为 AUC(Area Under ROC Curve)
对于有限个样本,显然可得
A
U
C
=
1
2
∑
i
=
1
m
−
1
(
x
i
+
1
−
x
i
)
∗
(
y
i
+
y
i
+
1
)
AUC = \frac{1}{2}\sum_{i=1}^{m-1} (x_{i+1} - x_i) * (y_i+y_{i+1})
AUC=21i=1∑m−1(xi+1−xi)∗(yi+yi+1)
AUC 考虑的是 样本预测的排序质量,因为它与排序误差有紧密联系。
给定 m+ 个正例和 m- 个反例,令D+ 和 D- 分别表示正、反例集合
则排序的 损失(loss) 定义为
l
r
a
n
k
=
1
m
+
m
−
∑
x
+
∈
D
+
∑
x
−
∈
D
−
(
[
f
(
x
+
)
<
f
(
x
−
)
]
+
1
2
[
f
(
x
+
)
=
f
(
x
−
)
]
)
l_{rank} = \frac{1}{m^+m^-}\sum_{x^+\in D^+}\sum_{x_-\in D^-}([f(x^+) < f(x^-)] + \frac{1}{2}[f(x^+)=f(x^-)])
lrank=m+m−1x+∈D+∑x−∈D−∑([f(x+)<f(x−)]+21[f(x+)=f(x−)])
其中,[] 方括号表示指示函数。[表达式],若表达式为真,为1;否则,为0
即,考虑每一对正反例,若正例的预测值小于反例,记 1个“罚分”,若相等记 0.5个 “罚分”
损失值对应的应该是 ROC 曲线的上部分面积:若一个正例在 ROC曲线 上对应标记点的坐标为(x, y),则 x 恰是排序在其之前的反例所占的比例,即假正率。可得
A
U
C
=
1
−
l
r
a
n
k
AUC = 1-l_{rank}
AUC=1−lrank
思考
为什么 损失率 是 ROC曲线 之上的面积?
因为 ROC曲线 是通过不断改变截断点得到的。如果正例排在反例之后,肯定会有一个截断点错误识别正反例。
同时,又因为 损失率定义的是每一对正反例,正好对应 ROC曲线上部面积 正反例排错所对应全部的重复的点
3.5 代价敏感错误率与代价曲线
预测结果假反例和假正例会造成不同程序的损失。例如把正常人预测为患者,把患者预测为正常人。前者只是增加了后续进一步检查的麻烦,但是后者可能会影响最佳救治时间。为了权衡不同类型错误造成的损失,可为错误赋予 非均等代价(unequal cost)。引入 代价矩阵
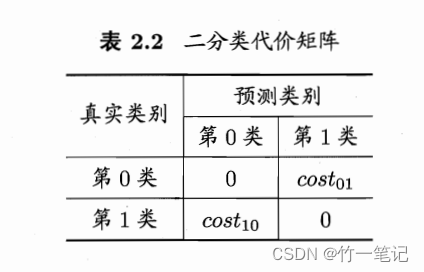
真正例和真反例的代价是0,因为是正确预测的。若假反例和假正例损失程度相差 越大,则cost10和cost01的值的差别越大。
我们之前介绍的所有内容,都隐式地假设了 均等代价,只考虑犯错的次数,不考虑不同错误会造成不同后果。在 非均等代价下,我们希望的不是犯错次数更少,而是犯错代价最小
若将 0 类作为正例,1类作为反例,令 D+ 和 D- 分别表示正例和反例子集,则 代价敏感(cost-sensitive) 错误率 为
E
(
f
;
D
;
c
o
s
t
)
=
1
m
(
∑
x
i
∈
D
+
[
(
f
(
x
i
≠
y
i
)
]
∗
c
o
s
t
01
+
∑
x
i
∈
D
−
[
(
f
(
x
i
≠
y
i
)
]
∗
c
o
s
t
10
)
E(f; D; cost) = \frac{1}{m}(\sum_{x_i\in D^+}[(f(x_i\not=y_i) ]* cost_{01} +\sum_{x_i\in D^-}[(f(x_i\not=y_i) ]* cost_{10})
E(f;D;cost)=m1(xi∈D+∑[(f(xi=yi)]∗cost01+xi∈D−∑[(f(xi=yi)]∗cost10)
类似可以给出 基于分布定义的代价敏感错误率 以及一些 性能度量的代价敏感版本
若令其中的 i j 不局限于 0 和 1,则可给出 多分类任务的代价敏感性能度量
在非均等代价下,ROC曲线 不能直接反应出学习器的期望总体代价,而代价曲线可以达到这个目的
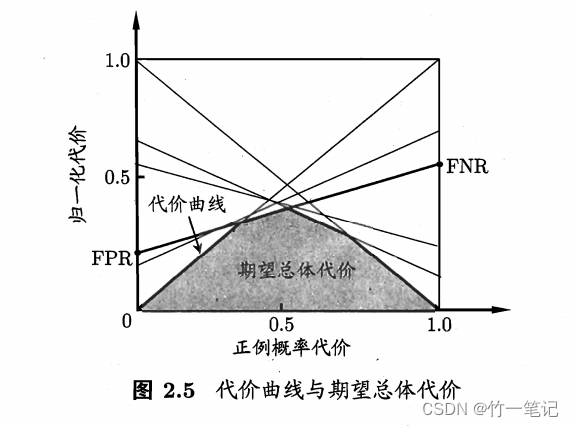
则正例代价显然可得
P
(
+
)
c
o
s
t
=
p
∗
c
o
s
t
01
p
∗
c
o
s
t
10
+
(
1
−
p
)
∗
c
o
s
t
10
P(+)cost = \frac{p * cost_{01}}{p*cost_{10} + (1-p) * cost_{10}}
P(+)cost=p∗cost10+(1−p)∗cost10p∗cost01
c
o
s
t
n
o
r
m
=
F
N
R
∗
p
∗
c
o
s
t
01
+
F
P
R
∗
(
1
−
p
)
∗
c
o
s
t
10
p
∗
c
o
s
t
01
+
(
1
−
p
)
∗
c
o
s
t
10
cost_{norm} = \frac{FNR * p *cost_{01} + FPR * (1-p) * cost_{10}}{p*cost_{01}+(1-p)*cost_{10}}
costnorm=p∗cost01+(1−p)∗cost10FNR∗p∗cost01+FPR∗(1−p)∗cost10
4. 比较检验
本节用
ϵ
\epsilon
ϵ :错误率(泛化错误率)
ϵ
^
\hat{\epsilon}
ϵ^ :测试错误率
4.1 假设检验
假设:根据测试集的 测试错误率 估推 泛化错误率
以下这部分内容公式我没看懂,贴原文希望以后能懂
原文:
4.2 交叉验证 t 检验
对于两个学习器 A 、B,使用 k 折交叉验证法测得两组错误率 1…k。若两个学习器的性能相同,则第 i 组测试集得到的测试错误率
ϵ
i
\epsilon_i
ϵi 也应该相同
对相同折下的错误率求差值:
Δ
i
=
ϵ
i
A
−
ϵ
i
B
\Delta_i = \epsilon^{A}_i - \epsilon^{B}_i
Δi=ϵiA−ϵiB。根据
Δ
1
.
.
.
Δ
k
\Delta_1... \Delta_k
Δ1...Δk 对 学习器A 与 学习器B 的性能相同 的假设做 t 检验,计算出差值的 均值
μ
\mu
μ 与 方差
σ
2
\sigma^2
σ2。
若
τ
t
=
∣
k
μ
σ
∣
\tau_t = \left| \frac{\sqrt k \mu}{\sigma} \right|
τt=
σkμ
小于临界值(2.7.1),则可认为两个学习器的性能没有差别。否则,平均错误率较小的学习器性能较优
交叉验证法不同轮次的训练集可能会有一定程度重叠,导致测试错误率实际上并不独立,会导致过高估计假设成立的概率。使用 5 x 2 交叉验证 法。做 5 次 2 折交叉验证,每次 2 折交叉验证前将随机数据打乱,使 5 次交验验证中的数据划分不重复。对学习器 A 和 B,分别在第 i 次 2 折交叉验证将产生的两对测试错误率分别求差。为缓解测试错误率的非独立性:
计算第 1 次 2 折交叉验证法产生的两个结果的平均值
计算第 2 折实验结果的方差


4.3 McNemar 检验

4.4 Friedman检验 与 Nemenyi后续检验
交叉验证t检验 和 McNemar检验 是同一数据集上比较 2 个算法的性能。若要比较多个算法性能,可以分别两两比较。或者使用 Friedman检验






5. 偏差与方差
偏差-方差分解(bias-variance decomposition):解释学习算法泛化性能
学习算法 的期望预测为:

假定噪声期望为 0,则泛化误差(省略推导过程):

可得,
泛化误差 = 偏差 + 方差 + 噪声
偏差:期望预测 与 真实结果的偏离程序
方差:度量同样大小训练集变动(数据扰动)千万的学习性能变化
噪声:学习算法能达到的期望泛化误差的下界
假定能控制学习算法的训练程度:
训练不足,拟合能力不够强,训练数据扰动不足以使学习器产生显著变化,此时偏差主导泛化错误率
训练加强,拟合能力增加,训练数据的扰动能被学习器学到,方差逐渐主导泛化错误率
训练充足后,学习器的拟合能力非常强,训练数据的轻微扰动都会导致学习器发生显著变化
若训练数据不重要的特性都被学习器学到了,则发生过拟合