1、计算机的起源
在19世纪的时候,“Computer”代表的并不是计算机,而是计算员,那时并没有计算机的概念,而计算员当然是要计算东西的,当时计算东西多,计算水平也参差不齐,加上疲劳等因素,很难保证每个人算出来的数据都准确,最后还要人工核对,消耗如此多的人力物力才能保证计算结果的准确性,这样查尔斯·巴贝奇(Charles Babbage)就该登场了。
1.1、机械时代
差分机
差分机(Difference Engine)是一种早期的机械计算设备,由英国数学家和发明家查尔斯·巴贝奇(Charles Babbage)在19世纪初设计。差分机的主要用途是计算多项式函数的值,以生成数表,例如航海和工程中的对数表和三角函数表。
它设计原理基于有限差分法(finite differences),这是一种数值方法,用于计算多项式的值,使用齿轮和杠杆来不断执行加法和减法运算,从而逐步生成所需的数值,它的重要性不仅在于它能够自动化地进行复杂的计算,更在于它是现代计算机科学发展的早期里程碑,尽管巴贝奇的差分机在他的一生中并未完全建成,但他的设计理念为后来的计算机发展奠定了基础。
程序
最早期的程序都是打孔纸带,是19世纪20年代,在一次工厂参观中,巴贝奇见到了由法国工程师约瑟夫·玛丽·雅卡尔(Joseph Marie Jacquard),在1804年发明的提花织布机,这种半自动的织布机有一条打孔纸带,随着纸带的滚动上面的孔洞会推动织布机的吊钩,从而自动织出不同花纹的布匹,这给了巴贝奇灵感,提花机的存在说明了机器能够理解人类的思维,所以巴贝奇将只能用来制表计算的差分机设计全部推翻,决心设计一种通用的数学计算器,也就是后来的分析机。
世界上公认的第一位程序员是阿达·洛芙莱斯(Ada Lovelace,1815年12月10日-1852年11月27日),是英国诗人乔治·戈登·拜伦(Lord Byron)的独生女,阿达于1833年认识了英国数学家和发明家查尔斯·巴贝奇,并对他的差分机(Difference Engine)和分析机(Analytical Engine)产生了浓厚兴趣。
她编写第一个计算机程序,在她的注释中,阿达描述了如何为分析机编写一个计算伯努利数(Bernoulli numbers)的算法,这个算法被认为是世界上第一个计算机程序,从而使她获得了“第一位程序员”的称号。
分析机
分析机(Analytical Engine)是由英国数学家和发明家查尔斯·巴贝奇(Charles Babbage)在19世纪中叶设计的一种早期机械计算设备,它被认为是世界上第一台通用计算机的概念模型,分析机的设计包括了现代计算机的许多基本概念,如存储器、中央处理器和输入输出设备,是现代计算机的先驱。
1.2电器时代
图灵机
图灵机(Turing Machine)是由英国数学家艾伦·图灵(Alan Turing)于1936年提出的一种抽象计算模型。图灵机是计算理论中的核心概念,用于形式化地定义计算和算法的概念,图灵机不仅在理论计算机科学中具有重要地位,也是现代计算机的理论基础。
2、平衡三进制基础门
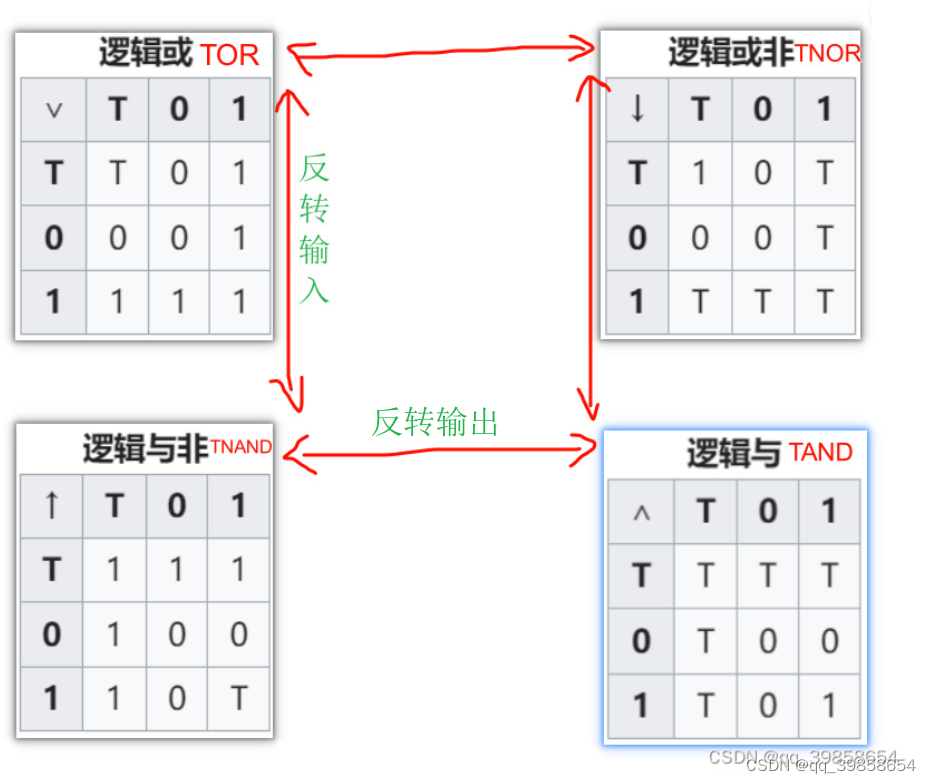
将会在原文章平衡三进制计算机中,不断的用新的编码,继续简化原来的设计,也会用到之前的平衡三进制摩根定律定律,这四个基础逻辑门分别是:TOR、TNOR、TNAND、TAND,它们的真值表是对称的,可通过如下图所示的对输入取反(垂直箭头)或对输出取反(水平箭头)来转换它们,如下图所示:
2.1平衡三进制新二进制编码
这种编码能用,发现这种编码弄出来的平衡三进制逻辑门所用的门更少,反正是能用更少的门完成原来的事了,同时输入输出也是标准的,如下所示:
| 二进制编码 | 平衡三进制表示 |
|---|---|
| 10 | T |
| 00 | 0 |
| 01 | 1 |
| 11 | 未使用,可用于纠错等 |
2.2平衡三进制逻辑非
如下所示,非的逻辑表示是要不要取反,当为00时要取反,而输入11时得到结果仍为00,得以下TNot组件,如下图所示:
| 逻辑非 | 转换表 | |
|---|---|---|
| T | 1 | 10---》01 |
| 0 | 0 | 00---》00 |
| 1 | T | 01---》10 |

2.3平衡三进制逻辑与门
平衡三进制逻辑与门:是有T出T、双1出1、其余为0,也就是可以分别判断三种情况,分别对其输出,如下所示:
| 逻辑与 | T | 0 | 1 |
|---|---|---|---|
| T | T | T | T |
| 0 | T | 0 | 0 |
| 1 | T | 0 | 1 |

2.4平衡三进制逻辑或门
平衡三进制逻辑或门:是有1出1、双T出T、其余为0,也就是可以分别判断三种情况,分别对其输出,如下所示:
| 逻辑或 | T | 0 | 1 |
|---|---|---|---|
| T | T | 0 | 1 |
| 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 |

2.5平衡三进制与非门
平衡三进制逻辑与非门:是有T出1、双1出T、其余为0,也就是可以分别判断三种情况,分别对其输出,如下所示:
| 逻辑与非 | T | 0 | 1 |
|---|---|---|---|
| T | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | T |

2.6平衡三进制或非门
平衡三进制逻辑或非门:是有1出T、双T出1、其余为0,也就是可以分别判断三种情况,分别对其输出,如下所示:
| 逻辑或非 | T | 0 | 1 |
|---|---|---|---|
| T | 1 | 0 | T |
| 0 | 0 | 0 | T |
| 1 | T | T | T |

2.7平衡三进制三与门
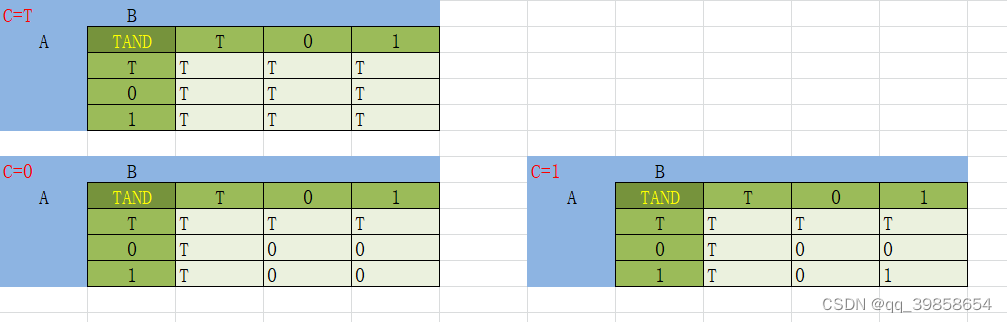
平衡三进制逻辑三与门:是有T出T、三1出1、其余为0,也就是可以分别判断三种情况,分别对其输出,如下所示:

2.8平衡三进制三或门
平衡三进制逻辑三或门:是有1出1、三T出T、其余为0,也就是可以分别判断三种情况,分别对其输出,如下所示:


3、平衡三进制基础门的扩展
3.1平衡三进制异或门
平衡三进制逻辑异或门:双T及双1出T、1T及T1出1、其余为0,也就是可以分别判断三种情况,分别对其输出,如下所示:
| 逻辑异或 | T | 0 | 1 |
|---|---|---|---|
| T | T | 0 | 1 |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | T |

3.2平衡三进制同或门
平衡三进制逻辑同或门:双T及双1出1、1T及T1出T、其余为0,也就是可以分别判断三种情况,分别对其输出,如下所示:
| 逻辑同或 | T | 0 | 1 |
|---|---|---|---|
| T | 1 | 0 | T |
| 0 | 0 | 0 | 0 |
| 1 | T | 0 | 1 |

3.3平衡三进制共识门
平衡三进制逻辑同或门:双T出T、双1出1、其余为0,也就是可以分别判断三种情况,分别对其输出,如下所示:
| 逻辑共识 | T | 0 | 1 |
|---|---|---|---|
| T | T | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |

3.4平衡三进制调和门
平衡三进制逻辑调和门:当为TT、0T、T0时出T,当为11、01、10时出1,其余为0,也就是分别判断有T及有1的情况,然后排除T1、1T就可得二种情况,分别对其输出,如下所示:
| 逻辑调和 | T | 0 | 1 |
|---|---|---|---|
| T | T | T | 0 |
| 0 | T | 0 | 1 |
| 1 | 0 | 1 | 1 |

3.5平衡三进制布尔基础件
这布尔转换件很好用,名称为3Mux-1,可以将平衡三进制的值转换成3组二进制的布尔值,无论在条件判断上,还是指令解释器中都很好用,如下表所示:
| 3MUx-1 | 二进制转换 |
|---|---|
| T | 100 |
| 0 | 010 |
| 1 | 001 |

3.6平衡三进制三态复用器
平衡三进制的三态多路复用器,详情请看平衡三进制全加器这文章,这组件可以让不同的输入从不同的端口进行输出,结合布尔基础件可得三态多路复用器,如下所示:
| 数据选择端 | 形成双向通路 |
|---|---|
| T | N端 到 输出端 |
| 0 | N端 到 输出端 |
| 1 | N端 到 输出端 |

3.7平衡三进制左偏门、右偏门
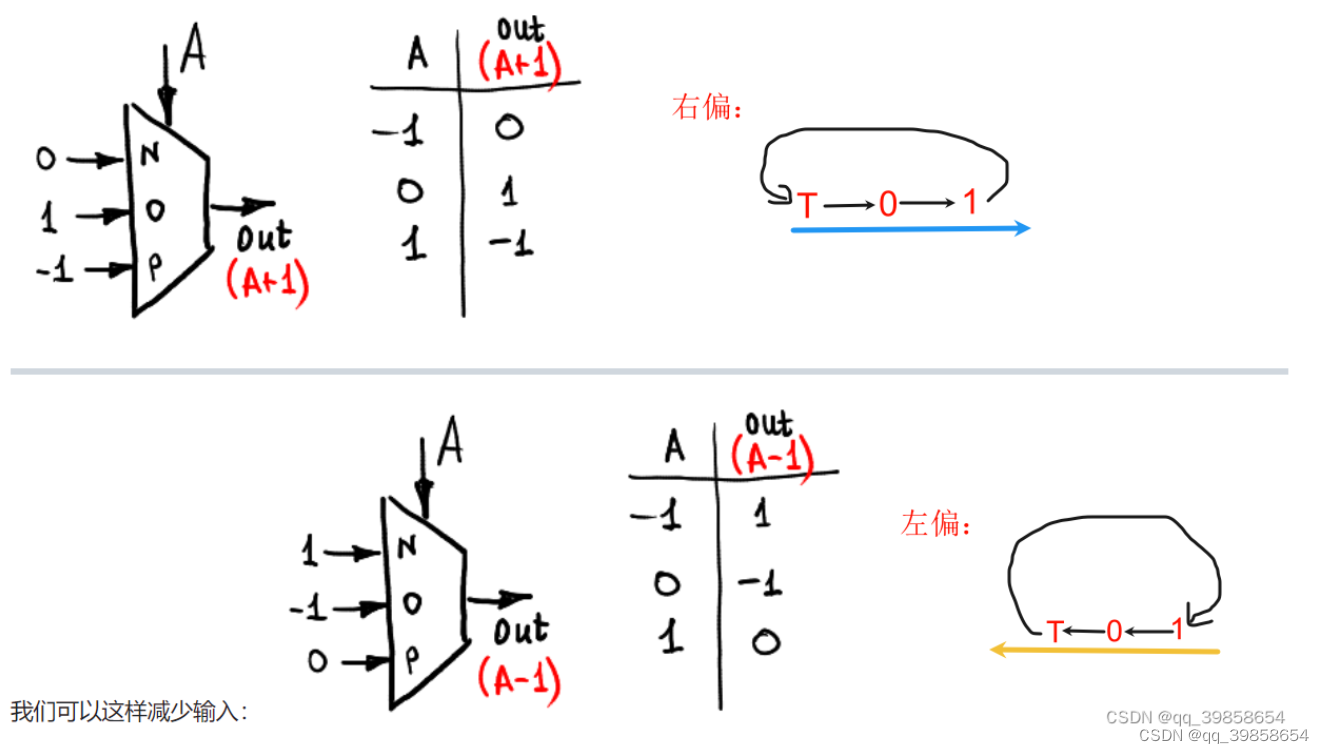
在选择全加器上有用到,可弄成基础件,从而转换输入简化输入,形成了(A+1)与(A-1)的输入,下面是输入输出真值表,如下所示:


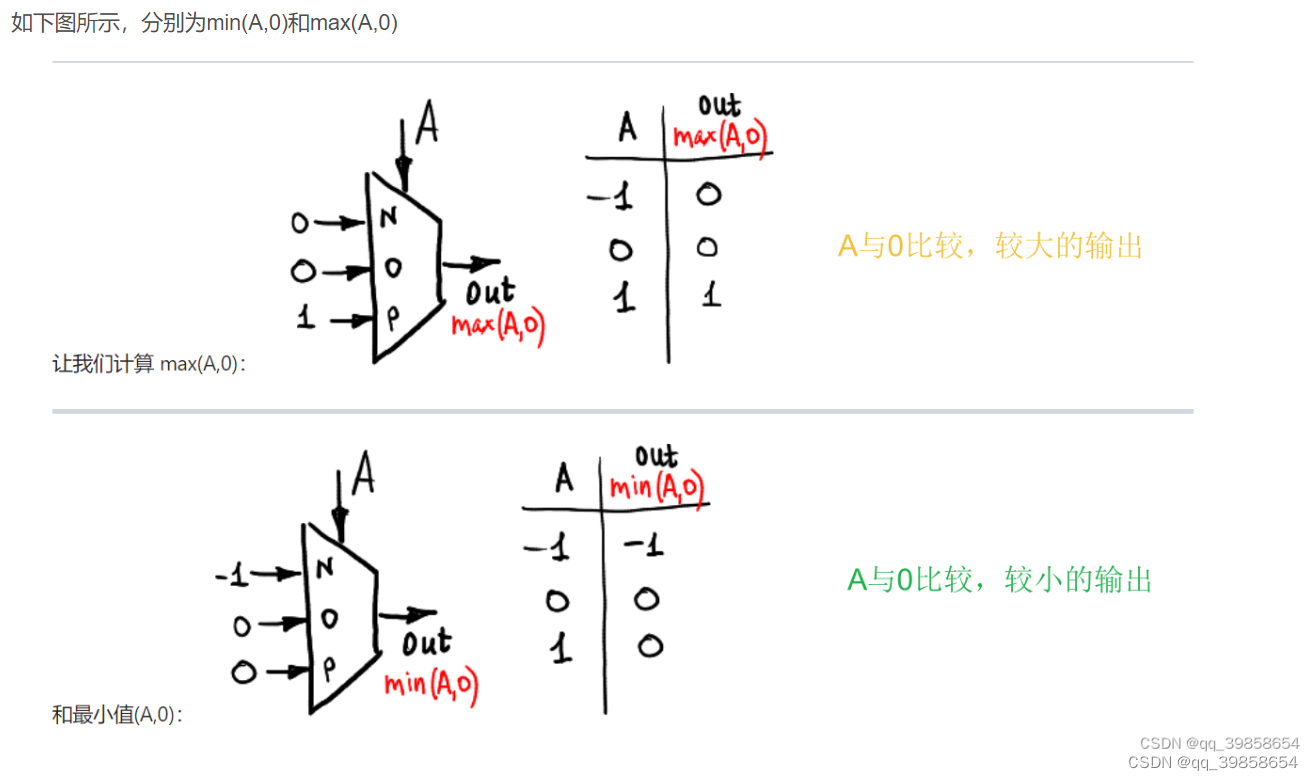
3.8平衡三进制最小门、最大门
在选择全加器上也有用到,可弄成基础件,从而转换输入简化输入,形成了Max(A,0)与Min(A,0),如下所示:


4、平衡三进制全加器
在文章平衡三进制全加器及平衡三进制计算机中,都用到了数据选择全加器,将进位位与加和位分开来实现,设计是很巧妙,但用二进制来模拟门还是太多了,即使后面做了优化,将平衡三进制半加器的中间表转换输出后,也只是从188个门降到了170个门,这与编码方式有关,但也与这种选择结构有关,如果没有原生实现这种组件,那确实导致门用太多不好化简的结果。
一开始就想像二进制的加法器同样设计,用1个异或门可以算出加和位,1个与门可以算出进位位,这样1个异或门和1个与门,可以组成一个半加器,而2个半加器及1个或门,可以组成1个全加器,而平衡三进制有没有这样的结构,是有的,当初的我道行不够推不出来,现在道行够了自然而然的就推出来了,推理过程如下:
4.1平衡三进制新的全加器
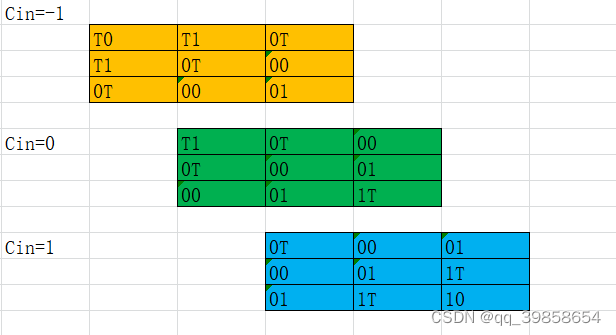
看上面的图,这是全加器的真值表,按照原来的思路是用平衡三进制的半加器,来组成平衡三进制的全加器,而平衡三进制与二进制不同,进位位不知如何处理,后面就放弃了这结构,直到今天又捡了起来,我们可以先分三组进行分析先,如下图所示:


通过上面的分析,可以看出当用两个平衡三进制半加器,将两个数相加后,加和位是固定下来了,而多了两个进位位,也会有运算,所以就再用一个平衡三进制半加器,这样就可以组成一个平衡三进制全加器了,如下图所示:

上面用了3个平衡三进制半加器,组成了1个平衡三进制全加器,然后分析一下,结合上面的手写的第二张图,进位位的运算有:T+1、0+T、T+0、0+1、1+0、1+T,输出只有加和位,不会有进位位的输出,也就说可以再优化,将进位位的半加器用什么门给代替掉,就可形成类似于二进制加法器的结构,可列出表格,如下所示:
| T | 0 | 1 | |
|---|---|---|---|
| T | T | 0 | |
| 0 | T | 0 | 1 |
| 1 | 0 | 1 |
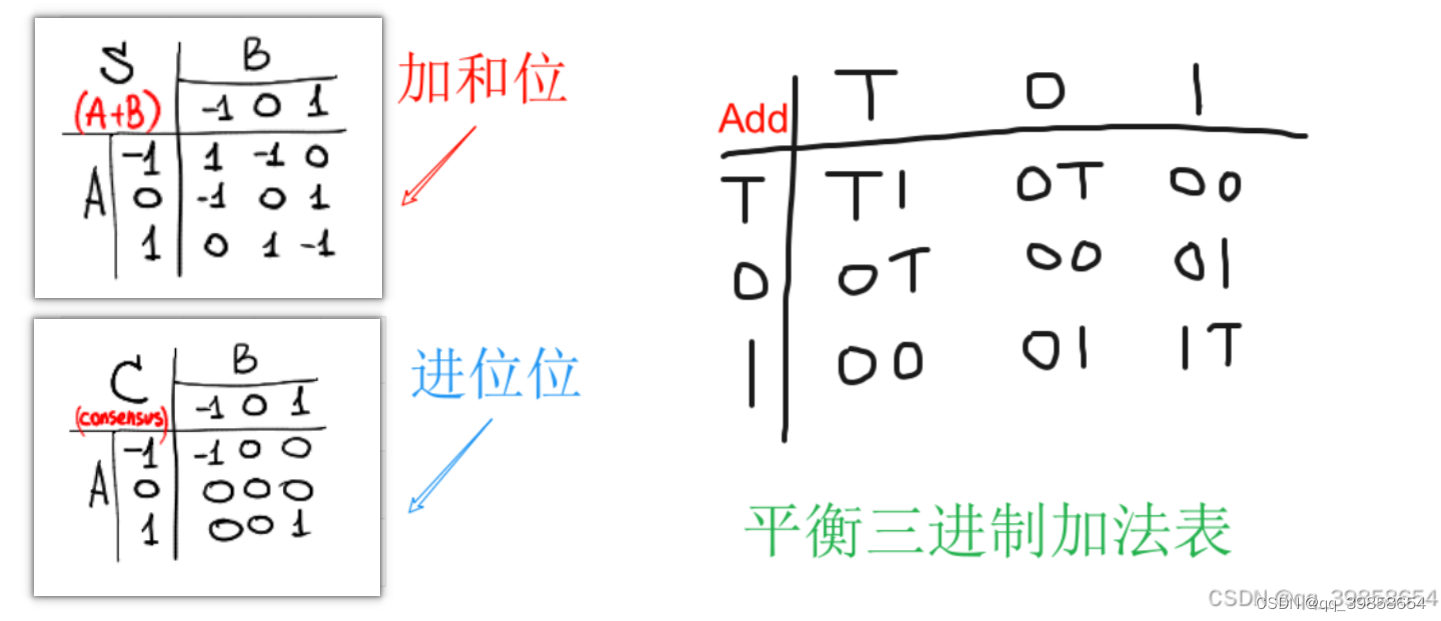
然后,你就会惊奇的发现,这上面的残缺的门跟平衡三进制调和门很像,如果深入下去就会发现,原来这平衡三进制的共识门和平衡三进制的调和门,分别是对应处理的是平衡三进制半加器的进位位及平衡三进制全加器的进位位,这波属实是破案了,难怪我一直不知这两个门有什么用,也一直没有加入进来,可能前苏联的三进制计算机的加法器,就是用了这种结构不然不会有这个门的真值表留了下来的,这样就提出了一种新的结构,用2个平衡三进制半加器及1个平衡三进制调和门组成一个平衡三进制全加器:

4.2平衡三进制半加器
平衡三进制半加器:加和位是(11、0T、T0)出T,(TT、01、10)出1,其余出0;进位位是TT出T,11出1,其余出0,也就是可以分别判断情况,分别对其输出,如下所示:

4.3平衡三进制全加器
平衡三进制逻辑全加器:由2个平衡三进制半加器及1个平衡三进制调和门组成,真值表如下,分别对其输出,如下所示:


4.4平衡三进制多位加法器(4Trit)
平衡三进制4trit的加法器,它可以计算(-81到81)以内的加减法,这是它的优点,加法器与减法器都是它,如下所示:

现在就可以试试它的计算功能了,如下图所示:

4.5平衡三进制多位加法器(8Trit)
平衡三进制8trit的加法器,它可以计算(-6561~6561)内的加减法,如果还不够可以继续串联,如下所示:

现在就可以试试它的计算功能了,如下图所示:

5、平衡三进制乘法器
平衡三进制的乘法也很简单,就像是两位十进制的数相乘,如:10*11=110,先分别相乘,然后相加就可以了,平衡三进制的乘法也是这样的;先是零乘任何数都为0,然后1*1与T*T结果都为1、最后是T*1或是1*T结果都为T,由此可列出表格;下面是平衡三进制乘法对照表,同时也是平衡三进制逻辑同或门的真值表,如下所示:
| Multiply | T | 0 | 1 |
|---|---|---|---|
| T | 1 | 0 | T |
| 0 | 0 | 0 | 0 |
| 1 | T | 0 | 1 |
5.1平衡三进制两位乘法器
这平衡三进制的乘法器,其实跟二进制的乘法器,结构差不多,只要把组件更换一下就行,了,可以看哔哩哔哩爱上半导体的视频讲解,下面是原理结构图,如下所示:

这样按照上的构思,平衡三进制两位乘法器就弄好了,可以算(-16~16)之间的正负乘法,可以扩展成更多位的,如下所示:

现在就可以试试它的计算功能了,如下图所示:

总结:
剩下的寄存器之间、多位或、多位乘法器等,你们可以看原来的平衡三进制计算机来设计,结构也太差不差,感觉确实可以弄一台出来玩,虽然真的没什么用,不过可以吹牛说这是一台三进制的计算机,用的也是三进制的逻辑,属实是装逼神器,你值得拥有。
参考资料:
1、Douglas W. Jones on Ternary Logic
2、维基百科-平衡三进制











![【2024最新华为OD-C/D卷试题汇总】[支持在线评测] 中文分词模拟器(200分) - 三语言AC题解(Python/Java/Cpp)](https://i-blog.csdnimg.cn/direct/563238f533cc4f3b8e6d812d064adbf1.png)