汉明权重（Hamming Weight）（统计数据中1的个数）VP-SWAR算法

news2024/11/26 5:27:09

汉明权重（Hamming Weight）（统计数据中1的个数）VP-SWAR算法

定义

汉明重量是一串符号中非零符号的个数。它等于同样长度的全零符号串的汉明距离(在信息论中，两个等长字符串之间的汉明距离等于两个字符串对应位置的不同字符的个数)。
汉明重量在常见的数据位符号串中，它是1的个数。

算法思想

基于分治的算法，将n位二进制进行分组，通过一系列位移和位运算操作，可以在常数时间内计算多个字节的汉明重量，并且不需要使用额外的内存。

简化示例

假设一个8bit的2进制串 x=abcd,efgh其中a-b 属于{0,1}
求解的输出是 ans = a+b+c+d+e+f+g+h

step1. 2bits m1= 0101 0101

x&m1 = 0b0d 0f0h
(x>>1)&m1 = 0a0c 0e0g
求和得到0[a+b]0[c+d] 0[e+f]0[g+h]，这里[x]表示二进制中1的个数

step2. 4bits m2 = 0011 0011

x&m2 = 000[c+d] 000[g+h]
(x>>2)&m2 = 000[a+b] 000[e+f]
求和得到000[a+b+c+d] 000[e+f+g+h]

step3. 8bits m4 = 0000 1111

x&m4 = 0000 000[e+f+g+h]
(x>>4)&m4 = 0000 000[a+b+c+d]
求和得到 [a+b+c+d+e+f+g+h]

算法实现 variable-precision SWAR算法

const uint64_t m1  = 0x5555555555555555; //binary: 0101...
const uint64_t m2  = 0x3333333333333333; //binary: 00110011..
const uint64_t m4  = 0x0f0f0f0f0f0f0f0f; //binary:  4 zeros,  4 ones ...
const uint64_t m8  = 0x00ff00ff00ff00ff; //binary:  8 zeros,  8 ones ...
const uint64_t m16 = 0x0000ffff0000ffff; //binary: 16 zeros, 16 ones ...
const uint64_t m32 = 0x00000000ffffffff; //binary: 32 zeros, 32 ones
const uint64_t h01 = 0x0101010101010101; //the sum of 256 to the power of 0,1,2,3...

//This is a naive implementation, shown for comparison,
//and to help in understanding the better functions.
//This algorithm uses 24 arithmetic operations (shift, add, and).
// 朴素算法
int popcount64a(uint64_t x)
{
    x = (x & m1 ) + ((x >>  1) & m1 ); //put count of each  2 bits into those  2 bits 
    x = (x & m2 ) + ((x >>  2) & m2 ); //put count of each  4 bits into those  4 bits 
    x = (x & m4 ) + ((x >>  4) & m4 ); //put count of each  8 bits into those  8 bits 
    x = (x & m8 ) + ((x >>  8) & m8 ); //put count of each 16 bits into those 16 bits 
    x = (x & m16) + ((x >> 16) & m16); //put count of each 32 bits into those 32 bits 
    x = (x & m32) + ((x >> 32) & m32); //put count of each 64 bits into those 64 bits 
    return x;
}

详细步骤

详细步骤
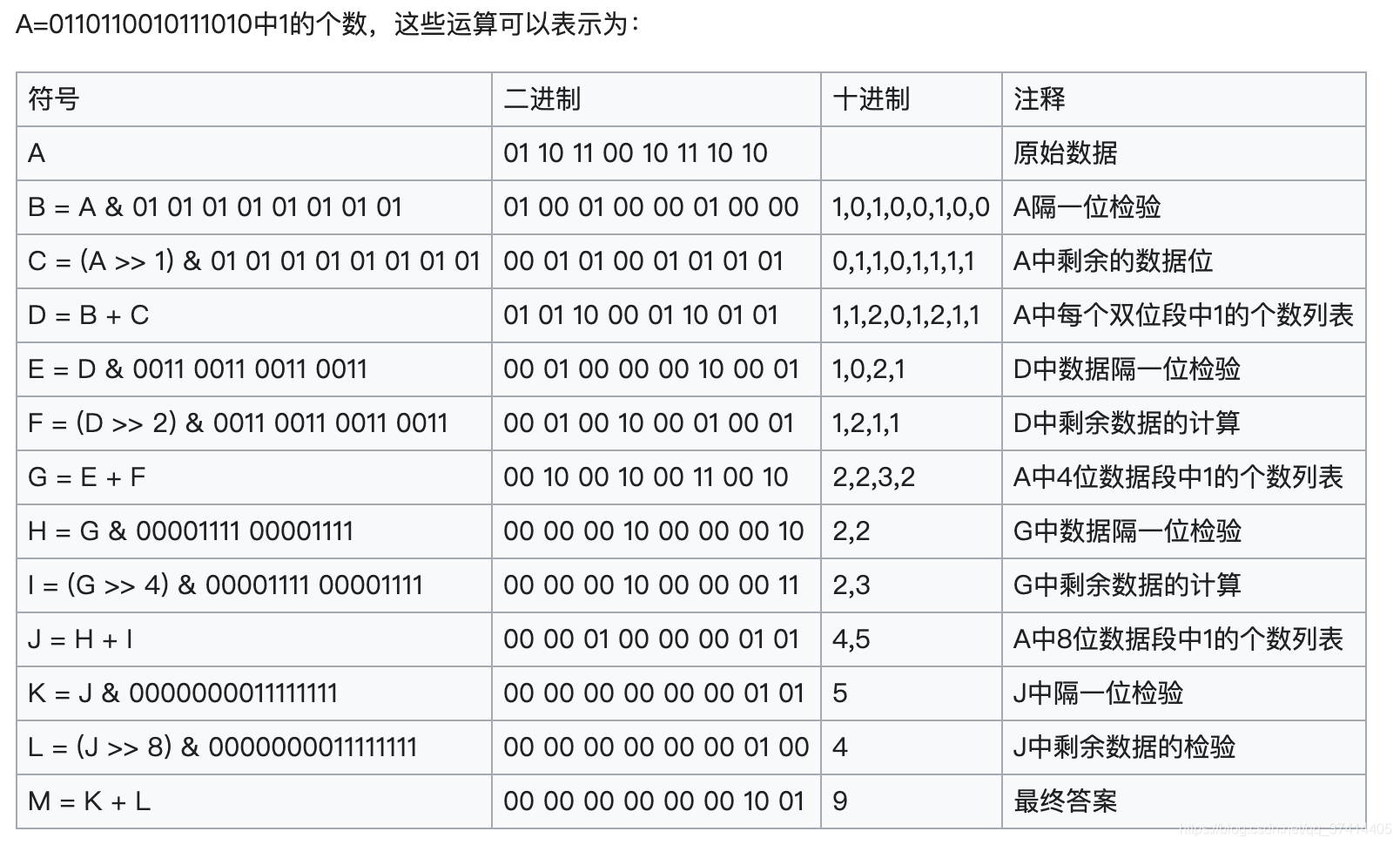
优化算法

//This is better when most bits in x are 0
//This algorithm works the same for all data sizes.
//This algorithm uses 3 arithmetic operations and 1 comparison/branch per "1" bit in x.
// 适用于0比较多的数
// 数字 n中最低位的 1 总是对应 n - 1 中的 0
// 将 n 和 n - 1 进行与运算总是能把 n 中最低位的 1 变成 0，并保持其他位不变
int popcount64d(uint64_t x)
{
    int count;
    for (count=0; x; count++)
        x &= x - 1;
    return count;
}

// 常用写法
int hammingWeight(uint32_t n) {
    int count = 0;
    
    while( n ){
        count ++;
        n &= n-1;
    }
    
    return count;
}

// 查表法 用空间换时间 从而得到O(1)的最优算法
以4bit的串为例，可以构造一个数组int counts[16]={0,1,1,2,1,2,2,3,1,2,2,3,2,3,3,4}.
对于4bit的x,x的hamming weight即为：counts[x].
static unsigned char wordbits[65536] = { bitcounts of ints between 0 and 65535 };
static int popcount(uint32 i)
{
    return (wordbits[i&0xFFFF] + wordbits[i>>16]);
}