问题描述

在一个 𝑛 行 𝑚列的矩阵王国中，生活着一些整数，其中一些是素数，一些不是素数。如果一个素数的上下左右、左上、右上、左下、右下相邻的数中都没有素数，我们就认为这是一个孤独的素数。

比如：一个 3行 5 列的矩阵如下。

3 8 10 9 5
6 10 2 4 13
8 8 9 6 3

这个矩阵中有 2 个素数，分别是第 1 行第 1 列的 3，和第 2 行第 3列的 2 。

请编程计算出，一个 𝑛 行 𝑚 列的矩阵中有多少个孤独的素数？

输入

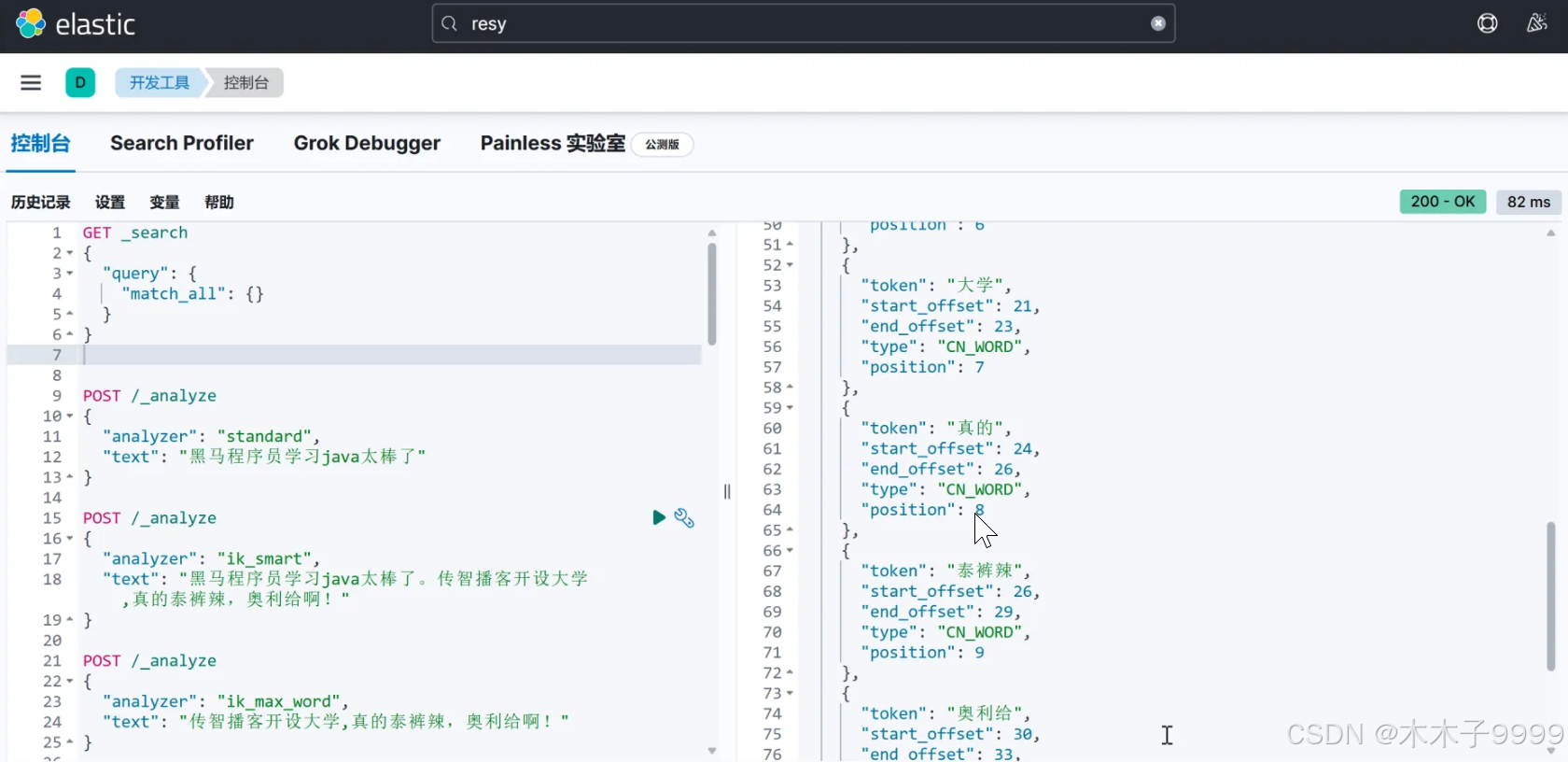
第 1 行有 2 个整数 n 和 m ，代表矩阵的大小（3≤𝑛,𝑚≤50）。

接下来 𝑛n 行，每行有 𝑚m 个整数（这些整数是 1∼1000 之间的整数，含 1 和 1000 ）

输出

输出 1个整数，代表矩阵中孤独素数的个数。

样例

输入

3 5
3 8 10 9 5
6 10 2 4 13
8 8 9 6 3

输出

2

附代码：

#include<iostream>
using namespace std;
int s[1010][1010];//定义一个比给定范围更大的矩阵 
int main()
{
    int n,m,sum=0,fss=0;//数据初始化，sum用来记录最终的素数总和，fss用来记录这个素数四面八方的不为素数的个数 
    cin>>n>>m;
    for(int i=1;i<=n;i++)//从1开始生成这个矩阵 
    {
        for(int j=1;j<=m;j++)
        {
            cin>>s[i][j];
        }
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            for(int x=2;x<=s[i][j];x++)//依次判断这个矩阵中的当前数据是否为素数 
            {
                if(s[i][j]==x)//如果为素数则判断该素数8个方向的其他数据是否全都不是素数 
                {
                //    sum++;
                //    cout<<s[i][j]<<" ";
                    for(int a=i-1;a<i+2;a++)//挨个遍历以该素数为中心的一个3*3的矩阵中的数据是否全都不是素数 
                    {
                        for(int b=j-1;b<j+2;b++)
                        {
                            for(int c=2;c<=s[a][b];c++)
                            {
                                if(s[a][b]==c)//如果有一个为素数则直接跳出 
                                {
                                    break;
                                }
                                if(s[a][b]%c==0)//如果被整除了说明它不是素数,是非素数 
                                {
                                    fss++;//则这个数据+1 
                                }
                            }
                            if(fss==8)//这个素数周围的8个数据都判断完后再来判定不是素数的个数一共有多少个，如果加起来有8个 
                            {
                                sum++;//则说明这是一个孤独的素数，则孤独素数总和+1； 
                                fss=0;//清零，重新开始第二数据的判断，重新判断第二个素数周围有多少个不是素数的个数 
                                //cout<<s[i][j]<<" "; 
                            }
                        }
                    }    
                }
                if(s[i][j]%x==0)//如果余数为0,则不为素数，直接跳出 
                break;
            }            
        }
    }
    cout<<sum;//最后输出孤独的素数总和共为多少个 
    return 0;
}