递归、dfs、回溯、剪枝，一针见血的

news2025/1/11 23:36:45

一、框架：

回溯搜索的遍历过程：回溯法⼀般是在集合中递归搜索，集合的⼤⼩构成了树的宽度，递归的

深度构成的树的深度。

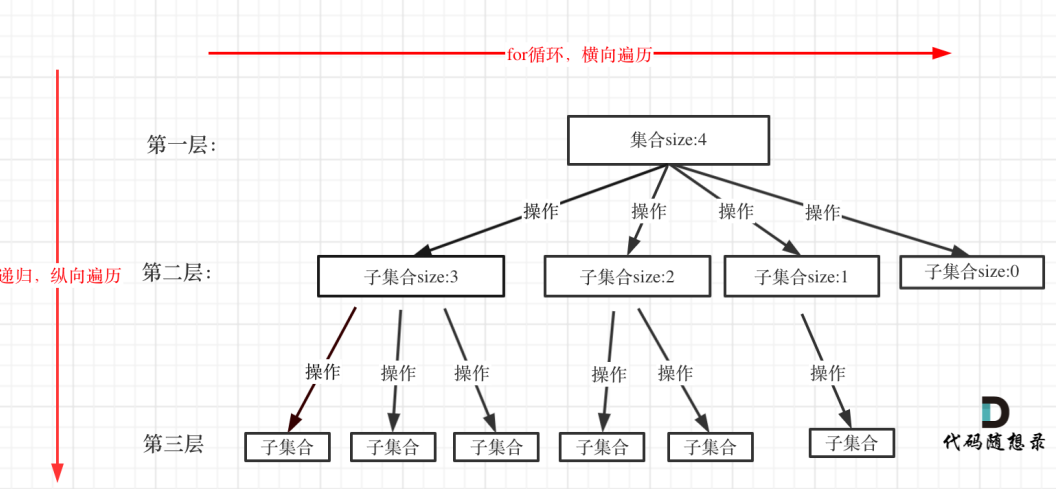
for循环就是遍历集合区间，可以理解⼀个节点有多少个孩⼦，这个for循环就执⾏多少次。

backtracking这⾥⾃⼰调⽤⾃⼰，实现递归。

⼤家可以从图中看出for循环可以理解是横向遍历，backtracking（递归）就是纵向遍历，

这样就把这棵树全遍历完了，⼀般来说，搜索叶⼦节点就是找的其中⼀个结果了。

分析完过程，回溯算法模板框架如下：

二、题目举例

1、组合问题

第77题. 组合

题⽬链接：https://leetcode-cn.com/problems/combinations/

给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数的组合。

⽰例:

输⼊: n = 4, k = 2

输出:

[

[2,4],

[3,4],

[2,3],

[1,2],

[1,3],

[1,4],

]

思路

也可以直接看我的B站视频：带你学透回溯算法-组合问题（对应⼒扣题⽬：77.组合）

本题这是回溯法的经典题⽬。

直接的解法当然是使⽤for循环，例如⽰例中k为2，很容易想到 ⽤两个for循环，这样就可以

输出 和⽰例中⼀样的结果。代码如下：

int n = 4;
for (int i = 1; i <= n; i++) {
 for (int j = i + 1; j <= n; j++) {
 cout << i << " " << j << endl;
 }
}

输⼊：n = 100, k = 3

那么就三层for循环，代码如下：

int n = 100;
for (int i = 1; i <= n; i++) {
 for (int j = i + 1; j <= n; j++) {
 for (int u = j + 1; u <= n; n++) {
 cout << i << " " << j << " " << u << endl;
 }
 }
}

如果n为100，k为50呢，那就50层for循环，此时就会发现虽然想暴⼒搜索，但是⽤for循环嵌套连暴⼒都写不出来！

咋整？

回溯搜索法来了，虽然回溯法也是暴⼒，但⾄少能写出来，不像for循环嵌套k层让⼈绝望。

那么回溯法怎么暴⼒搜呢？

上⾯我们说了要解决 n为100，k为50的情况，暴⼒写法需要嵌套50层for循环，那么回溯法就⽤递归来解决嵌套层数的问题。

递归来做层叠嵌套（可以理解是开k层for循环），每⼀次的递归中嵌套⼀个for循环，那么

递归就可以⽤于解决多层嵌套循环的问题了。此时递归的层数⼤家应该知道了，例如：n为100，k为50的情况下，就是递归50层。

如果脑洞模拟回溯搜索的过程，绝对可以让⼈窒息，所以需要抽象图形结构来进⼀步理解。

回溯法解决的问题都可以抽象为树形结构（N叉树），⽤树形结构来理解回溯就容易多了。

那么我把组合问题抽象为如下树形结构：

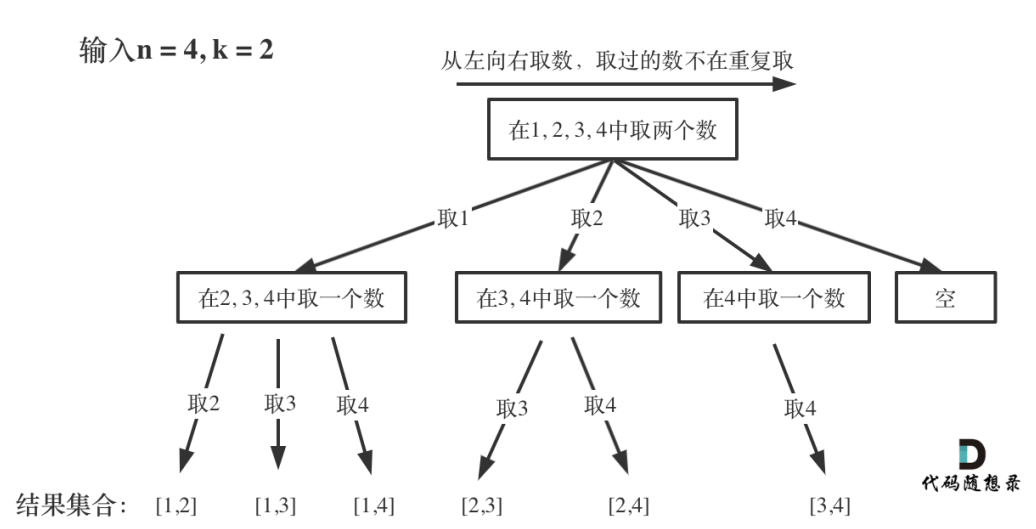
可以看出这个棵树，⼀开始集合是 1，2，3，4， 从左向右取数，取过的数，不在重复取。

第⼀次取1，集合变为2，3，4 ，因为k为2，我们只需要再取⼀个数就可以了，分别取2，

3，4，得到集合[1,2] [1,3] [1,4]，以此类推。

每次从集合中选取元素，可选择的范围随着选择的进⾏⽽收缩，调整可选择的范围。

图中可以发现n相当于树的宽度，k相当于树的深度。

总结：递归的第1层：选数都是从1开始选；递归的第2层：选数都是从2开始选，k为2的时候选两个数，所以树的高度为两层，因此k为多少，树的高度就为多少。

重点来了，那么如何在这个树上遍历，然后收集到我们要的结果集呢？

图中每次搜索到了叶⼦节点，我们就找到了⼀个结果。

相当于只需要把达到叶⼦节点的结果收集起来，就可以求得 n个数中k个数的组合集合。

重点又来了，如何用代码实现呢？

思路：

函数⾥⼀定有两个参数，既然是集合n⾥⾯取k的数，那么n和k是两个int型的参数。

然后还需要⼀个参数，为int型变量startIndex，这个参数⽤来记录本层递归的中，集合从哪

⾥开始遍历（集合就是[1,...,n] ）。

为什么要有这个startIndex呢？

每次从集合中选取元素，可选择的范围随着选择的进⾏⽽收缩，调整可选择的范围，就是要

靠startIndex。

从下图中红线部分可以看出，在集合[1,2,3,4]取1之后，下⼀层递归，就要在[2,3,4]中取数

了，那么下⼀层递归如何知道从[2,3,4]中取数呢，靠的就是startIndex。

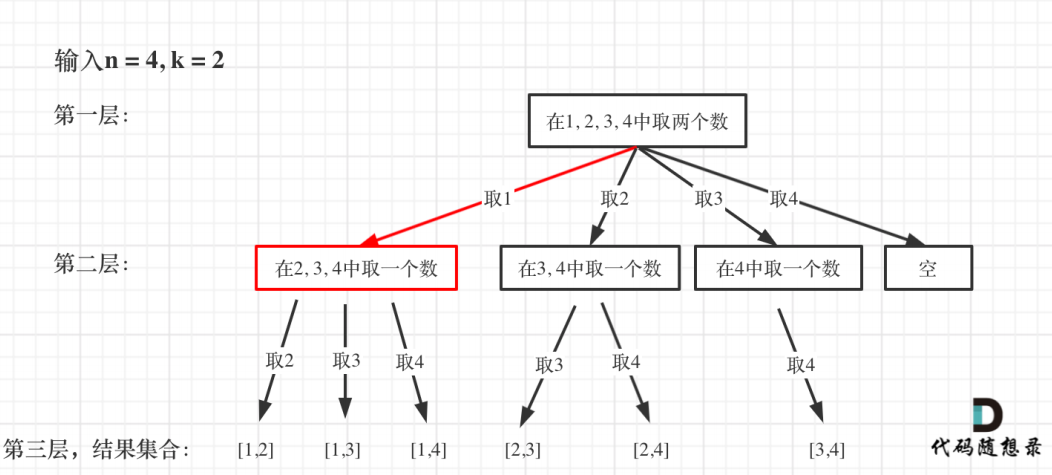
所以需要startIndex来记录下⼀层递归，搜索的起始位置。

步骤：

（1）回溯函数终⽌条件

什么时候到达所谓的叶⼦节点了呢？

path这个数组的⼤⼩如果达到k，说明我们找到了⼀个⼦集⼤⼩为k的组合了，在图中path

存的就是根节点到叶⼦节点的路径。

如图红⾊部分：

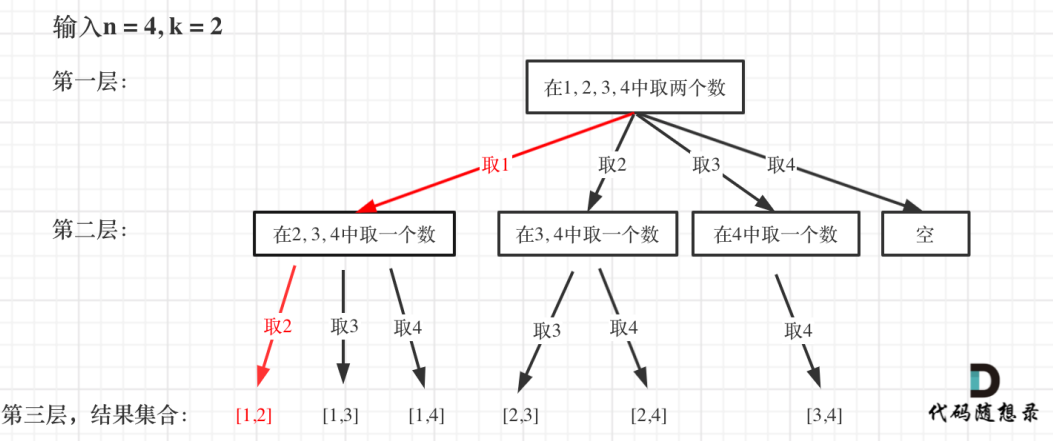
if(path.size() == k)
{
     for(int i = 0 ; i < path.size(); i ++)  out.printf("%d",path.get(i));
     out.println();
     out.flush();
     return;
}

（2）单层搜索的过程

回溯法的搜索过程就是⼀个树型结构的遍历过程，在如下图中，可以看出for循环⽤来横向

遍历，递归的过程是纵向遍历。

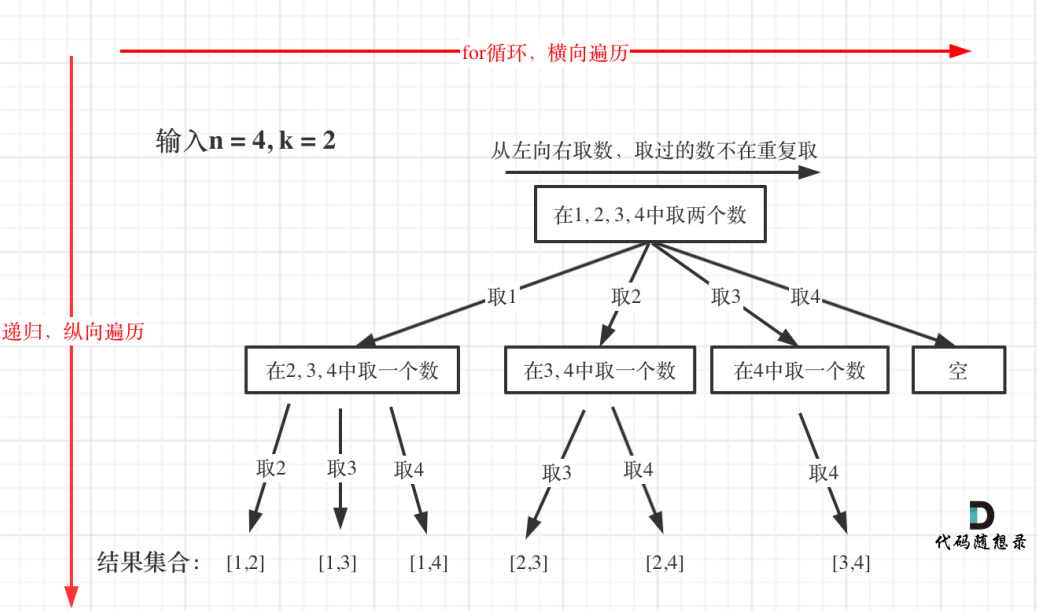
如此我们才遍历完图中的这棵树。

for循环每次从startIndex开始遍历，然后⽤path保存取到的节点i。

for(int i = startIndex ; i <= n ; i ++)
{
     // 变长数组的add是每一次都是从变长数组的最后添加一个元素
     path.add(i);
     // 不用打标记的原因就是：只要选了一个，i ++，选的数字都是递增的，序列是递增的
     dfs(n, k, i + 1);
     // 恢复现场，弹出刚才添加到路径的数
     path.remove(path.size() - 1);
}

可以看出dfs（递归函数）通过不断调⽤⾃⼰⼀直往深处遍历，总会遇到叶⼦节

点，遇到了叶⼦节点就要返回。

完整的dfs代码：

static void dfs(int n,int k,int startIndex)
{
    if(path.size() == k)
    {
        for(int i = 0 ; i < path.size(); i ++)  out.printf("%d",path.get(i));
        out.println();
        out.flush();
        return;
    }
        
    for(int i = startIndex ; i <= n ; i ++)
    {
         // 变长数组的add是每一次都是从变长数组的最后添加一个元素
         path.add(i);
         // 不用打标记的原因就是：只要选了一个，i ++，选的数字都是递增的，序列是递增的
         dfs(n, k, i + 1);
         // 恢复现场，弹出刚才添加到路径的数
         path.remove(path.size() - 1);
     }
}

实操代码：

package hly;

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.math.BigInteger;
import java.nio.file.attribute.AclEntryFlag;
import java.security.AlgorithmConstraints;
import java.text.DateFormatSymbols;
import java.util.ArrayList;
import java.util.List;
import java.util.StringTokenizer;
import java.util.Vector;

class in 
{
    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
    static StringTokenizer tokenizer = new StringTokenizer("");
    
    static String nextLine() throws IOException   { return reader.readLine(); }
    
    static String next() throws IOException 
    {
        while (!tokenizer.hasMoreTokens())  tokenizer = new StringTokenizer(reader.readLine());
        return tokenizer.nextToken();
    }

    static int nextInt() throws IOException  { return Integer.parseInt(next()); }

    static double nextDouble() throws IOException { return Double.parseDouble(next()); }
    
    static long nextLong() throws IOException  { return Long.parseLong(next());}
    
    static BigInteger nextBigInteger() throws IOException 
    { 
        BigInteger d = new BigInteger(in.nextLine());
        return d;
    }
}

public class 组合问题 
{
    static int N = 100;
    static int n;
    static PrintWriter out = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out))); 
    //动态数组存路径可太行了
    static List<Integer> path = new ArrayList<>();
    
     static void dfs(int n,int k,int startIndex)
    {
        if(path.size() == k)
        {
            for(int i = 0 ; i < path.size(); i ++)  out.printf("%d",path.get(i));
            out.println();
            out.flush();
            return;
        }
        
        for(int i = startIndex ; i <= n ; i ++)
        {
            // 变长数组的add是每一次都是从变长数组的最后添加一个元素
            path.add(i);
            // 不用打标记的原因就是：只要选了一个，i ++，选的数字都是递增的，序列是递增的
            dfs(n, k, i + 1);
            // 恢复现场，弹出刚才添加到路径的数
            path.remove(path.size() - 1);
        }
    }
    
    public static void main(String[] args) throws IOException 
    {
         int n = in.nextInt();
         int k = in.nextInt();
         
         // 
         dfs(n,k,1);
         out.flush();
    }
}

剪枝优化：

来举⼀个例⼦，n = 4，k = 4的话，那么第⼀层for循环的时候，从元素2开始的遍历都没有

意义了。 在第⼆层for循环，从元素3开始的遍历都没有意义了。

这么说有点抽象，如图所⽰：

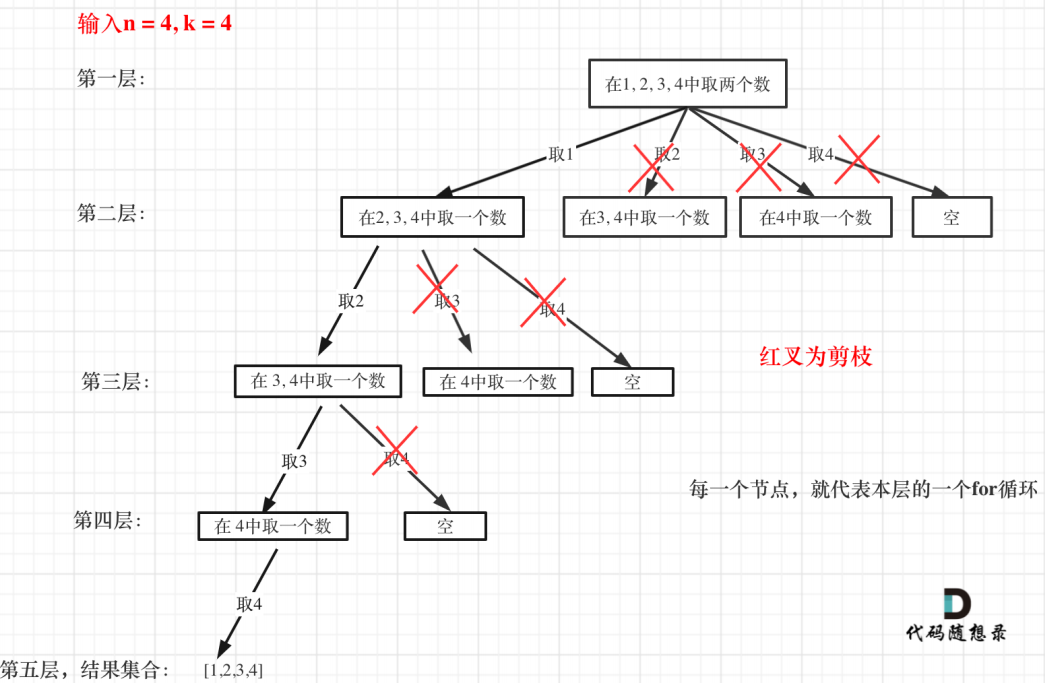
图中每⼀个节点（图中为矩形），就代表本层的⼀个for循环，那么每⼀层的for循环从第⼆

个数开始遍历的话，都没有意义，都是⽆效遍历。

所以，可以剪枝的地⽅就在递归中每⼀层的for循环所选择的起始位置。

如果for循环选择的起始位置之后的元素个数 已经不⾜ 我们需要的元素个数了，那么就没有

必要搜索了。

原来的for循环代码：

for(int i = startIndex ; i <= n ; i ++)

接下来看⼀下优化过程如下：

1. 已经选择的元素个数：path.size();

2. 还需要的元素个数为: k - path.size();

3. 在集合n中⾄多要从该起始位置 : n - (k - path.size()) + 1，开始遍历

为什么有个+1呢，因为包括起始位置，我们要是⼀个左闭的集合。

举个例⼦，n = 4，k = 3， ⽬前已经选取的元素为0（path.size为0），n - (k - 0) + 1 即 4 - (3 - 0) + 1 = 2。

从2开始搜索都是合理的，可以是组合[2, 3, 4]。

这⾥⼤家想不懂的话，建议也举⼀个例⼦，就知道是不是要+1了。

所以优化之后的for循环是：

for(int i = startIndex ; i <=  n - (k - path.size()) + 1 ; i ++)

实操：

package hly;

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.math.BigInteger;
import java.nio.file.attribute.AclEntryFlag;
import java.security.AlgorithmConstraints;
import java.text.DateFormatSymbols;
import java.util.ArrayList;
import java.util.List;
import java.util.StringTokenizer;
import java.util.Vector;

class in 
{
    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
    static StringTokenizer tokenizer = new StringTokenizer("");
    
    static String nextLine() throws IOException   { return reader.readLine(); }
    
    static String next() throws IOException 
    {
        while (!tokenizer.hasMoreTokens())  tokenizer = new StringTokenizer(reader.readLine());
        return tokenizer.nextToken();
    }

    static int nextInt() throws IOException  { return Integer.parseInt(next()); }

    static double nextDouble() throws IOException { return Double.parseDouble(next()); }
    
    static long nextLong() throws IOException  { return Long.parseLong(next());}
    
    static BigInteger nextBigInteger() throws IOException 
    { 
        BigInteger d = new BigInteger(in.nextLine());
        return d;
    }
}

public class 组合问题 
{
    static int N = 100;
    static int n;
    static PrintWriter out = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out))); 
    //动态数组存路径可太行了
    static List<Integer> path = new ArrayList<>();
    
     static void dfs(int n,int k,int startIndex)
    {
        if(path.size() == k)
        {
            for(int i = 0 ; i < path.size(); i ++)  out.printf("%d",path.get(i));
            out.println();
            out.flush();
            return;
        }
        
        for(int i = startIndex ; i <=  n - (k - path.size()) + 1 ; i ++)
        {
            // 变长数组的add是每一次都是从变长数组的最后添加一个元素
            path.add(i);
            // 不用打标记的原因就是：只要选了一个，i ++，选的数字都是递增的，序列是递增的
            dfs(n, k, i + 1);
            // 恢复现场，弹出刚才添加到路径的数
            path.remove(path.size() - 1);
        }
    }
    
    public static void main(String[] args) throws IOException 
    {
         int n = in.nextInt();
         int k = in.nextInt();
         
         // 
         dfs(n,k,1);
         out.flush();
    }
}

二、组合总和（⼀）

问题：找出在[1,2,3,...，n]这个集合中找到和为target的k个数的组合。

相对于回溯算法：求组合问题！，⽆⾮就是多了⼀个限制，本题是要找到和为target的k个数的组合，想到这⼀点了，做过77. 组合之后，本题是简单⼀些了。

本题k相当于了树的深度，9（因为整个集合就是9个数）就是树的宽度。例如 k = 2，n = 4的话，就是在集合[1,2,3,...，n]中求 k（个数） = 2, target（和） = 4的组合。

选取过程如图：

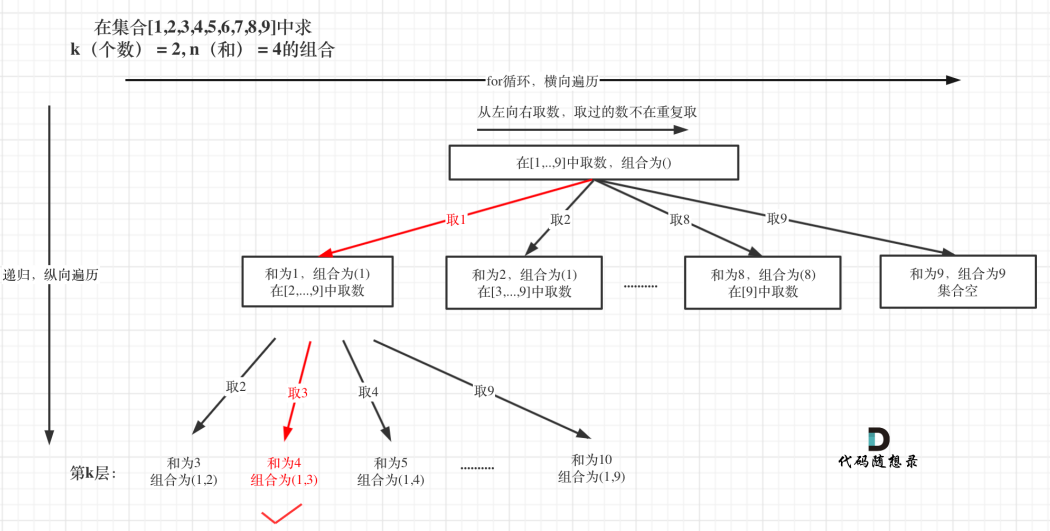
简简单单，只有和的约束，和上题几乎相同，直接上代码

package hly;

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.math.BigInteger;
import java.nio.file.attribute.AclEntryFlag;
import java.security.AlgorithmConstraints;
import java.text.DateFormatSymbols;
import java.util.ArrayList;
import java.util.List;
import java.util.StringTokenizer;
import java.util.Vector;

class in 
{
    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
    static StringTokenizer tokenizer = new StringTokenizer("");
    
    static String nextLine() throws IOException   { return reader.readLine(); }
    
    static String next() throws IOException 
    {
        while (!tokenizer.hasMoreTokens())  tokenizer = new StringTokenizer(reader.readLine());
        return tokenizer.nextToken();
    }

    static int nextInt() throws IOException  { return Integer.parseInt(next()); }

    static double nextDouble() throws IOException { return Double.parseDouble(next()); }
    
    static long nextLong() throws IOException  { return Long.parseLong(next());}
    
    static BigInteger nextBigInteger() throws IOException 
    { 
        BigInteger d = new BigInteger(in.nextLine());
        return d;
    }
}

public class 组合问题 
{
    static int N = 100;
    static int n;
    static int k;
    static int target;
    static int sum = 0;
    static PrintWriter out = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out))); 
    //动态数组存路径可太行了
    static List<Integer> path = new ArrayList<>();
    
     static void dfs(int n,int k,int target, int startIndex)
    {
        if(path.size() == k)
        {
            if(sum == target)
            {
                for(int i = 0 ; i < path.size(); i ++)  out.printf("%d",path.get(i));
                out.println();
                out.flush();
                return;
            }
            return;
        }
        
        for(int i = startIndex ; i <=  n - (k - path.size()) + 1 ; i ++)
        {
            // 变长数组的add是每一次都是从变长数组的最后添加一个元素
            path.add(i);        
            sum += i;
            // 不用打标记的原因就是：只要选了一个，i ++，选的数字都是递增的，序列是递增的
            dfs(n, k,target, i + 1);
            // 恢复现场，弹出刚才添加到路径的数
            path.remove(path.size() - 1);
            sum -= i;
        }
    }
    
    public static void main(String[] args) throws IOException 
    {
         n = in.nextInt();
         k = in.nextInt();
         target = in.nextInt();
         
         // 
         dfs(n,k,target,1);
         out.flush();
    }
}

剪汁儿来辣！

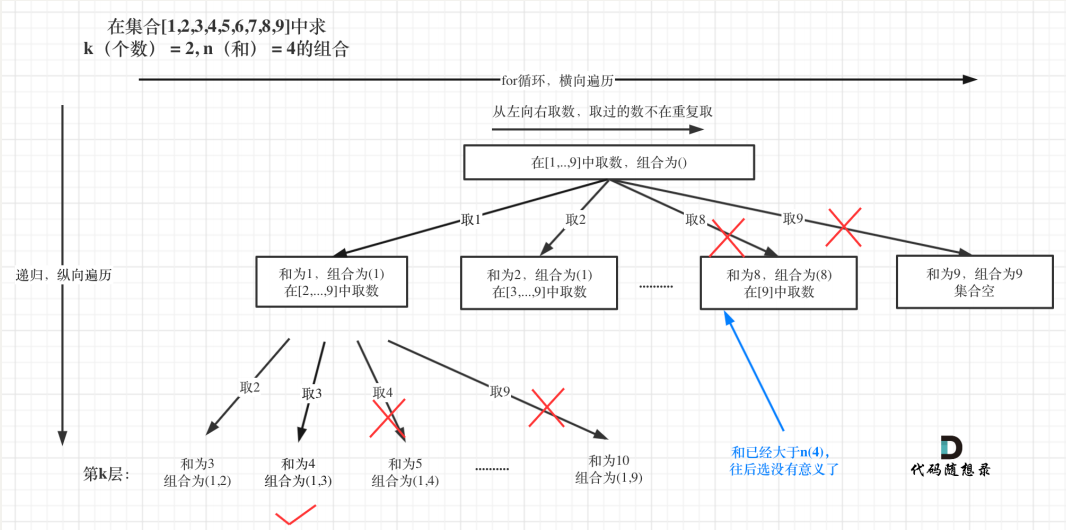
观察图得，已选元素总和如果已经⼤于n（图中数值为4）了，但是还不够k个，那么往后遍历就没有意义了，直接剪掉。剪枝的地⽅⼀定是在递归终⽌的地⽅剪，剪枝代码如下：

if(sum > target)  return;

实操：

package hly;

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.math.BigInteger;
import java.nio.file.attribute.AclEntryFlag;
import java.security.AlgorithmConstraints;
import java.text.DateFormatSymbols;
import java.util.ArrayList;
import java.util.List;
import java.util.StringTokenizer;
import java.util.Vector;

class in 
{
    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
    static StringTokenizer tokenizer = new StringTokenizer("");
    
    static String nextLine() throws IOException   { return reader.readLine(); }
    
    static String next() throws IOException 
    {
        while (!tokenizer.hasMoreTokens())  tokenizer = new StringTokenizer(reader.readLine());
        return tokenizer.nextToken();
    }

    static int nextInt() throws IOException  { return Integer.parseInt(next()); }

    static double nextDouble() throws IOException { return Double.parseDouble(next()); }
    
    static long nextLong() throws IOException  { return Long.parseLong(next());}
    
    static BigInteger nextBigInteger() throws IOException 
    { 
        BigInteger d = new BigInteger(in.nextLine());
        return d;
    }
}

public class 组合问题 
{
    static int N = 100;
    static int n;
    static int k;
    static int target;
    static int sum = 0;
    static PrintWriter out = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out))); 
    //动态数组存路径可太行了
    static List<Integer> path = new ArrayList<>();
    
     static void dfs(int n,int k,int target, int startIndex)
    {
         if(sum > target)  return;
         
        if(path.size() == k)
        {
            if(sum == target)
            {
                for(int i = 0 ; i < path.size(); i ++)  out.printf("%d",path.get(i));
                out.println();
                out.flush();
                return;
            }
            return;
        }
        
        for(int i = startIndex ; i <=  n - (k - path.size()) + 1 ; i ++)
        {
            // 变长数组的add是每一次都是从变长数组的最后添加一个元素
            path.add(i);        
            sum += i;
            // 不用打标记的原因就是：只要选了一个，i ++，选的数字都是递增的，序列是递增的
            dfs(n, k,target, i + 1);
            // 恢复现场，弹出刚才添加到路径的数
            path.remove(path.size() - 1);
            sum -= i;
        }
    }
    
    public static void main(String[] args) throws IOException 
    {
         n = in.nextInt();
         k = in.nextInt();
         target = in.nextInt();
         
         // 
         dfs(n,k,target,1);
         out.flush();
    }
}

变种1：（好像更简单了）

问题：找出在[1,2,3，...，n]这个集合中找到和为staget的组合。（组合的元素没有个数限制、组合内元素不能重复）

代码：

package hly;

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.math.BigInteger;
import java.nio.file.attribute.AclEntryFlag;
import java.security.AlgorithmConstraints;
import java.text.DateFormatSymbols;
import java.util.ArrayList;
import java.util.List;
import java.util.StringTokenizer;
import java.util.Vector;

class in 
{
    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
    static StringTokenizer tokenizer = new StringTokenizer("");
    
    static String nextLine() throws IOException   { return reader.readLine(); }
    
    static String next() throws IOException 
    {
        while (!tokenizer.hasMoreTokens())  tokenizer = new StringTokenizer(reader.readLine());
        return tokenizer.nextToken();
    }

    static int nextInt() throws IOException  { return Integer.parseInt(next()); }

    static double nextDouble() throws IOException { return Double.parseDouble(next()); }
    
    static long nextLong() throws IOException  { return Long.parseLong(next());}
    
    static BigInteger nextBigInteger() throws IOException 
    { 
        BigInteger d = new BigInteger(in.nextLine());
        return d;
    }
}

public class 组合问题 
{
    static int N = 100;
    static int n;
    static int k;
    static int target;
    static int sum = 0;
    static PrintWriter out = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out))); 
    //动态数组存路径可太行了
    static List<Integer> path = new ArrayList<>();
    
     static void dfs(int n,int target, int startIndex)
    {
         if(sum > target)  return;
         
        if(sum == target)
        {
            for(int i = 0 ; i < path.size(); i ++)  out.printf("%d",path.get(i));
            out.println();
            out.flush();
            return;
        }
        
        
        for(int i = startIndex ; i <=  n ; i ++)
        {
            // 变长数组的add是每一次都是从变长数组的最后添加一个元素
            path.add(i);        
            sum += i;
            // 不用打标记的原因就是：只要选了一个，i ++，选的数字都是递增的，序列是递增的
            dfs(n,target, i + 1);
            // 恢复现场，弹出刚才添加到路径的数
            path.remove(path.size() - 1);
            sum -= i;
        }
    }
    
    public static void main(String[] args) throws IOException 
    {
         n = in.nextInt();
         target = in.nextInt();
         
         dfs(n,target,1);
         out.flush();
    }
}

变种2：

问题：找出在[1,2,3，...，n]这个集合中找到和为target的组合。（组合的元素没有个数限制、组合内元素可以重复）

相较于上边的变种1：dfs(n,target, i + 1);改为dfs(n,target, i );其余代码相同
真是妙哎~

代码：

package hly;

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.math.BigInteger;
import java.nio.file.attribute.AclEntryFlag;
import java.security.AlgorithmConstraints;
import java.text.DateFormatSymbols;
import java.util.ArrayList;
import java.util.List;
import java.util.StringTokenizer;
import java.util.Vector;

class in 
{
    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
    static StringTokenizer tokenizer = new StringTokenizer("");
    
    static String nextLine() throws IOException   { return reader.readLine(); }
    
    static String next() throws IOException 
    {
        while (!tokenizer.hasMoreTokens())  tokenizer = new StringTokenizer(reader.readLine());
        return tokenizer.nextToken();
    }

    static int nextInt() throws IOException  { return Integer.parseInt(next()); }

    static double nextDouble() throws IOException { return Double.parseDouble(next()); }
    
    static long nextLong() throws IOException  { return Long.parseLong(next());}
    
    static BigInteger nextBigInteger() throws IOException 
    { 
        BigInteger d = new BigInteger(in.nextLine());
        return d;
    }
}

public class 组合问题 
{
    static int N = 100;
    static int n;
    static int k;
    static int target;
    static int sum = 0;
    static PrintWriter out = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out))); 
    //动态数组存路径可太行了
    static List<Integer> path = new ArrayList<>();
    
     static void dfs(int n,int target, int startIndex)
    {
         if(sum > target)  return;
         
        if(sum == target)
        {
            for(int i = 0 ; i < path.size(); i ++)  out.printf("%d",path.get(i));
            out.println();
            out.flush();
            return;
        }
        
        
        for(int i = startIndex ; i <=  n ; i ++)
        {
            // 变长数组的add是每一次都是从变长数组的最后添加一个元素
            path.add(i);        
            sum += i;
            // 不用打标记的原因就是：只要选了一个，i ++，选的数字都是递增的，序列是递增的
            dfs(n,target, i);
            // 恢复现场，弹出刚才添加到路径的数
            path.remove(path.size() - 1);
            sum -= i;
        }
    }
    
    public static void main(String[] args) throws IOException 
    {
         n = in.nextInt();
         target = in.nextInt();
         
         dfs(n,target,1);
         out.flush();
    }
}

变种3：

问题：找出在长度为n的数组a（无重复元素）中找到和为target的组合。（组合的元素没有个数限制、组合内元素可以重复、组合间允许重复）

⽰例 1：

输⼊：n = 4，candidates = [2,3,6,7], target = 7,

所求解集为：

[

[7],

[2,2,3]

]

⽰例 2：

输⼊：n = 3，candidates = [2,3,5], target = 8,

所求解集为：

[

[2,2,2,2],

[2,3,3],

[3,5]

]

注意图中叶⼦节点的返回条件，因为本题没有组合数量要求，仅仅是总和的限制，所以递归

没有层数的限制，只要选取的元素总和超过target，就返回！

⽽在第一个问题中都可以知道要递归K层，因为要取k个元素的组合。

本题还需要startIndex来控制for循环的起始位置，对于组合问题，什么时候需要

startIndex呢？

我举过例⼦，如果是⼀个集合来求组合的话，就需要startIndex，例如：回溯算法：求组合

问题！，回溯算法：求组合总和！。

如果是多个集合取组合，各个集合之间相互不影响，那么就不⽤startIndex，例如：回溯算

法：电话号码的字母组合

注意以上我只是说求组合的情况，如果是排列问题，又是另⼀套分析的套路，后⾯我再讲解

排列的时候就重点介绍。

package hly;

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.math.BigInteger;
import java.nio.file.attribute.AclEntryFlag;
import java.security.AlgorithmConstraints;
import java.text.DateFormatSymbols;
import java.util.ArrayList;
import java.util.List;
import java.util.StringTokenizer;
import java.util.Vector;

class in 
{
    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
    static StringTokenizer tokenizer = new StringTokenizer("");
    
    static String nextLine() throws IOException   { return reader.readLine(); }
    
    static String next() throws IOException 
    {
        while (!tokenizer.hasMoreTokens())  tokenizer = new StringTokenizer(reader.readLine());
        return tokenizer.nextToken();
    }

    static int nextInt() throws IOException  { return Integer.parseInt(next()); }

    static double nextDouble() throws IOException { return Double.parseDouble(next()); }
    
    static long nextLong() throws IOException  { return Long.parseLong(next());}
    
    static BigInteger nextBigInteger() throws IOException 
    { 
        BigInteger d = new BigInteger(in.nextLine());
        return d;
    }
}

public class 组合问题 
{
    static PrintWriter out = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out))); 
    
    static int N = 100;
    static int n;
    static int k;
    static int target;
    static int sum = 0;
    static int a[] = new int[N];
    
    //动态数组存路径可太行了
    static List<Integer> path = new ArrayList<>();
    
     static void dfs(int target, int startIndex)
    {
         if(sum > target)  return;
         
        if(sum == target)
        {
            for(int i = 0 ; i < path.size(); i ++)  out.printf("%d",path.get(i));
            out.println();
            out.flush();
            return;
        }
        
        
        for(int i = startIndex ; i < n ; i ++)
        {
            path.add(a[i]);        
            sum += a[i];
            
            dfs(target, i);
           
            path.remove(path.size() - 1);
            sum -= a[i];
        }
    }
    
    public static void main(String[] args) throws IOException 
    {
         n = in.nextInt();
         for(int i = 0 ; i < n ; i ++)  a[i] = in.nextInt();
         target = in.nextInt();
         
         dfs(target,0);
         out.flush();
    }
}

剪枝优化：

在这个树形结构中：

对于sum已经⼤于target的情况，其实是依然进⼊

了下⼀层递归，只是下⼀层递归结束判断的时候，会判断sum > target的话就返回。

其实如果已经知道下⼀层的sum会⼤于target，就没有必要进⼊下⼀层递归了。

那么可以在for循环的搜索范围上做做⽂章了。

对总集合排序之后，如果下⼀层的sum（就是本层的 sum + candidates[i]）已经⼤于

target，就可以结束本轮for循环的遍历。

如图：

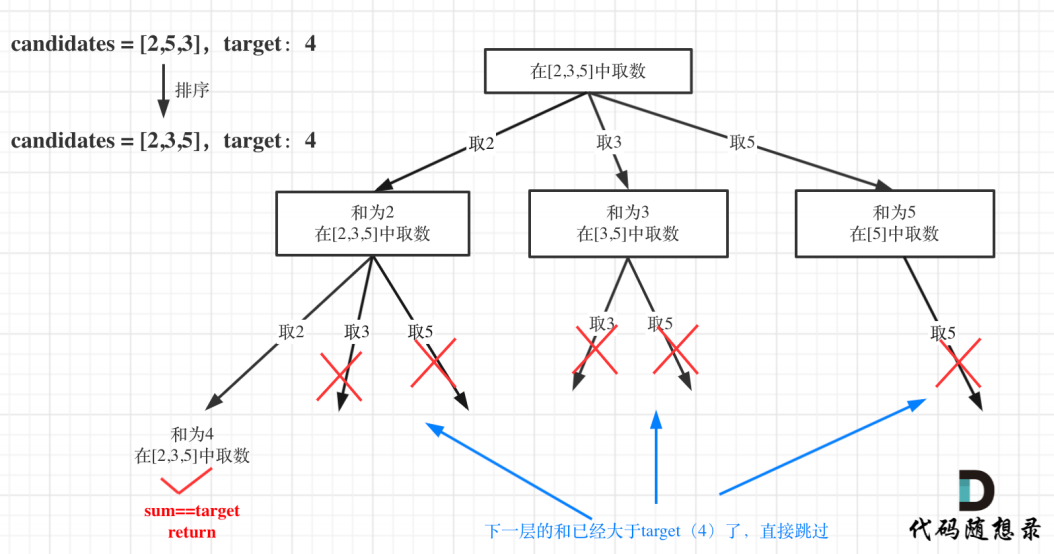
for循环剪枝代码如下：

for(int i = startIndex ; i < n && sum + a[i] <= target ; i ++)

实操：

package hly;

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.math.BigInteger;
import java.nio.file.attribute.AclEntryFlag;
import java.security.AlgorithmConstraints;
import java.text.DateFormatSymbols;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.StringTokenizer;
import java.util.Vector;

class in 
{
    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
    static StringTokenizer tokenizer = new StringTokenizer("");
    
    static String nextLine() throws IOException   { return reader.readLine(); }
    
    static String next() throws IOException 
    {
        while (!tokenizer.hasMoreTokens())  tokenizer = new StringTokenizer(reader.readLine());
        return tokenizer.nextToken();
    }

    static int nextInt() throws IOException  { return Integer.parseInt(next()); }

    static double nextDouble() throws IOException { return Double.parseDouble(next()); }
    
    static long nextLong() throws IOException  { return Long.parseLong(next());}
    
    static BigInteger nextBigInteger() throws IOException 
    { 
        BigInteger d = new BigInteger(in.nextLine());
        return d;
    }
}

public class 组合问题 
{
    static PrintWriter out = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out))); 
    
    static int N = 100;
    static int n;
    static int k;
    static int target;
    static int sum = 0;
    static int a[] = new int[N];
    
    //动态数组存路径可太行了
    static List<Integer> path = new ArrayList<>();
    
     static void dfs(int target, int startIndex)
    {    
        if(sum > target)  return;

        if(sum == target)
        {
            for(int i = 0 ; i < path.size(); i ++)  out.printf("%d",path.get(i));
            out.println();
            out.flush();
            return;
        }
        
        // 如果 sum + a[i] > target 就终⽌遍历
        for(int i = startIndex ; i < n && sum + a[i] <= target ; i ++)
        {
            path.add(a[i]);        
            sum += a[i];
            
            dfs(target, i);
            
            path.remove(path.size() - 1);
            sum -= a[i];
        }
    }
    
    public static void main(String[] args) throws IOException 
    {
         n = in.nextInt();
         for(int i = 0 ; i < n ; i ++)  a[i] = in.nextInt();
         target = in.nextInt();
         
         Arrays.sort(a,0,n);
         dfs(target,0);
         out.flush();
    }
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/193843.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

那些提升工作效率的Windows常用快捷键

那些提升工作效率的Windows常用快捷键

那些提升工作效率的Windows常用快捷键 前言 在我们日常工作中&#xff0c;掌握一些常用的电脑快捷键&#xff0c;可以让办公效率事半功倍&#xff0c;熟用快捷键可以极大增加我们的工作效率&#xff0c;更重要的是键盘操作看起来更让人赏心悦目&#xff01; 我们通常将快捷键…
阅读更多...
【C++】作用域与函数重载

【C++】作用域与函数重载

【C】作用域与函数重载 1、作用域 1.1 作用域的作用 作用域——scope 通常来说&#xff0c;一段程序代码中所用到的名字并不总是有效/可用的&#xff0c;而限定这个名字的可用性的代码范围就是这个名字的作用域。 简单来说&#xff0c;作用域的使用减少了代码中名字的重复冲…
阅读更多...
13、稀疏矩阵

13、稀疏矩阵

目录 一、稀疏矩阵的生成 1.利用sparse函数建立一般的稀疏矩阵 2.利用特定函数建立稀疏矩阵 二、稀疏矩阵的运算 一、稀疏矩阵的生成 1.利用sparse函数建立一般的稀疏矩阵 稀疏矩阵指令的调用格式&#xff1a; 示例1&#xff1a;输入一个稀疏矩阵 Asparse([1 2 3 4 5],[…
阅读更多...
教你一招完美解决 pptx 库安装失败的问题

教你一招完美解决 pptx 库安装失败的问题

上一篇&#xff1a;Python的序列结构及常用操作方法&#xff0c;学完这一篇你就彻底懂了 文章目录前言一、pptx 库是什么&#xff1f;二、安装失败原因及解决方案总结前言 昨天有粉丝问我&#xff0c;为什么Python的 pptx 库老是安装失败&#xff1f;加上国内镜像源也不行&…
阅读更多...
分布式微服务2

分布式微服务2

目录 Nacos注册中心 下载 启动 快速入门 1.在父工程中添加spring-cloud-alilbaba的管理依赖子模块添加nacos的客户端依赖 2.子模块添加nacos的客户端依赖 3.子模块配置文件 4.启动 Nacos服务分级存储模型 集群配置 nacos的负载均衡 Nacos环境隔离 新建命名空间 N…
阅读更多...
六、Linux 软件包管理

六、Linux 软件包管理

一、Linux 软件包管理简介 1、软件包分类 源码包 - 脚本安装二进制包 -&#xff08;RPM 包&#xff0c; 系统默认包&#xff09; 2、源码包优缺点 源码包优点&#xff1a; 开源&#xff0c;可以看到&#xff0c;并且可以修改源代码。可以自由选择所需要的工能。软件是编译安…
阅读更多...
初识 Linux Shell

初识 Linux Shell

学习的第一步&#xff0c;就是要找到 Linux 终端的所在位置。目前较常见的图形化终端有 Konsole、Gnome terminal、xterm 等几种。一般安装后在各个发行版的菜单中搜索即可找到。Gnome terminal 和 Konsole 基本是当前各大流行 Linux 发行版预装最多的终端应用&#xff0c;功能…
阅读更多...
分时电价环境下用户负荷需求响应分析方法(Matlab代码实现）

分时电价环境下用户负荷需求响应分析方法(Matlab代码实现）

&#x1f4a5;&#x1f4a5;&#x1f49e;&#x1f49e;欢迎来到本博客❤️❤️&#x1f4a5;&#x1f4a5; &#x1f3c6;博主优势&#xff1a;&#x1f31e;&#x1f31e;&#x1f31e;博客内容尽量做到思维缜密&#xff0c;逻辑清晰&#xff0c;为了方便读者。 ⛳️座右铭&a…
阅读更多...
升级JDK11后,执行java -version还是1.8

升级JDK11后,执行java -version还是1.8

电脑同时安装两个JDK,如何来回切换1. JDK INSTALL1.1 Download1.2 配置环境变量2. 配置JDK11无效2.1 JDK切换3.Awakening1. JDK INSTALL 1.1 Download 官网下载 JDK Website: https://www.oracle.com/java/technologies/downloads/. oracle账密 zhaonan0212163.com Tomcat123…
阅读更多...
论文翻译：Text-based Image Editing for Food Images with CLIP

论文翻译：Text-based Image Editing for Food Images with CLIP

使用 CLIP 对食物图像进行基于文本的图像编辑 图1&#xff1a;通过文本对食品图像进行处理的结果示例。最左边一栏显示的是原始输入图像。"Chahan"&#xff08;日语中的炒饭&#xff09;和 "蒸饭"。左起第二至第六列显示了VQGAN-CLIP所处理的图像。每个操作…
阅读更多...
小程序项目学习--第六章：项目实战二、推荐歌曲-歌单展示-巅峰榜-歌单详情-页面优化

小程序项目学习--第六章：项目实战二、推荐歌曲-歌单展示-巅峰榜-歌单详情-页面优化

第六章&#xff1a;推荐歌曲-歌单展示-巅峰榜-歌单详情-页面优化 01_(掌握)音乐页面-推荐歌曲的数据获取和展示 推荐歌曲的数据获取的实现步骤 0.封装对应请求接口方法 export function getPlaylistDetail(id) {return hyRequest.get({url: "/playlist/detail",d…
阅读更多...
Python中append浅拷贝机制

Python中append浅拷贝机制

关于深浅拷贝&#xff0c;最直观的理解就是&#xff1a;深拷贝&#xff1a;拷贝的程度深&#xff0c;自己新开辟了一块内存&#xff0c;将被拷贝内容全部拷贝过来了&#xff1b;浅拷贝&#xff1a;拷贝的程度浅&#xff0c;只拷贝原数据的首地址&#xff0c;然后通过原数据的首…
阅读更多...
分享158个ASP源码，总有一款适合您

分享158个ASP源码，总有一款适合您

ASP源码 分享158个ASP源码&#xff0c;总有一款适合您 下面是文件的名字&#xff0c;我放了一些图片&#xff0c;文章里不是所有的图主要是放不下...&#xff0c; 158个ASP源码下载链接&#xff1a;https://pan.baidu.com/s/1DCXBAXJUNMZZpbyxVF5-bg?pwdbwuv 提取码&#x…
阅读更多...
react native android环境搭建，使用vscode和夜神模拟器进行开发（适用于0.68+版本）

react native android环境搭建，使用vscode和夜神模拟器进行开发（适用于0.68+版本）

前言 react native官网教程 使用的是android studio搭建环境&#xff0c;本篇文章使用vscode和夜神模拟器进行搭建环境 版本说明&#xff1a; 0.68.0 及以上版本直接往下看0.67.4 及以下版本请查看另一篇文章&#xff1a;react native android环境搭建&#xff0c;使用vscod…
阅读更多...
FineReport学习-【01 帆软报表入门】

FineReport学习-【01 帆软报表入门】

界面功能 官方管理面板详解见这里 报表简介 报表类型 报表设计流程 新建数据连接 查看数据库连接&#xff0c;新建一个本地mysql的数据库 新建报表 新建数据集 实例操作 实例1 分组报表 新建文件夹&#xff0c;用来保存报表 将刚刚查询的数据表放入报表中&#xff0c;并插入表…
阅读更多...
k8s核心资源ingress

k8s核心资源ingress

一、简介ingress是分装到service层上层的一个模块&#xff0c;对外提供统一访问入口&#xff0c;ingress底层是nginx实现的&#xff0c;并且分装了域名访问。外界请求首先打到ingress层&#xff0c;ingress再转发给service层&#xff0c;service再负载均衡到其中的一个pod上。i…
阅读更多...
关于符合车规的高精度定位产品

关于符合车规的高精度定位产品

文章目录一、什么是P-Box二、ST的P-Box三、导远的P-Box四、华测的P-Box参考来源对于导航产品来说&#xff0c;下一个大的市场可能就是智能驾驶/辅助驾驶&#xff0c;研发符合车规的导航产品也逐渐成了行业趋势。组合导航产品的主流方案是外置的P-Box方案&#xff0c;只需要单GN…
阅读更多...
excel定位选取：再谈快捷键Ctrl+G的妙用

excel定位选取：再谈快捷键Ctrl+G的妙用

一、仅复制可见单元格在日常工作中我们经常会涉及将隐藏或分类汇总后的数据&#xff0c;粘到一个新表。这个时候如果我们直接复制&#xff0c;粘贴会发生什么呢&#xff1f;这是一个分类汇总后的数据&#xff0c;自动生成了分级显示&#xff1a;第1级&#xff0c;总计&#xff…
阅读更多...
uniapp提交应用市场打包问题和安装应用弹出隐私政策协议问题（Android）

uniapp提交应用市场打包问题和安装应用弹出隐私政策协议问题（Android）

uni-app 安卓App提交到应用市场踩坑记录&#xff0c;隐私合规检测&#xff0c;参考链接&#xff1a;https://juejin.cn/post/7163595800235212830 打包问题&#xff0c;同时支持32位和64位&#xff1b;https://uniapp.dcloud.net.cn/tutorial/app-android-abifilters.html# 重…
阅读更多...
【Android Studio】【Flutter】Android Studio下Flutter环境搭建记录

【Android Studio】【Flutter】Android Studio下Flutter环境搭建记录

目录&#xff1a;1、要学flutter&#xff0c;必须先学Dart语言&#xff08;类似C语言&#xff09;2、下载Flutter SDK&#xff08;软件开发工具包&#xff09;3、配置国内镜像4、Android Studio新建Flutter项目5、问题解决&#xff1a;&#xff08;运行flutter doctor命令检查问…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023