3413. DHCP服务器

•    题目
•    提交记录
•    讨论
•    题解
•    视频讲解

动态主机配置协议（Dynamic Host Configuration Protocol, DHCP）是一种自动为网络客户端分配 IP 地址的网络协议。

当支持该协议的计算机刚刚接入网络时，它可以启动一个 DHCP 客户端程序。

后者可以通过一定的网络报文交互，从 DHCP 服务器上获得 IP 地址等网络配置参数，从而能够在用户不干预的情况下，自动完成对计算机的网络设置，方便用户连接网络。

DHCP 协议的工作过程如下：

1. 当 DHCP 协议启动的时候，DHCP 客户端向网络中广播发送 Discover 报文，请求 IP 地址配置；
2. 当 DHCP 服务器收到 Discover 报文时，DHCP 服务器根据报文中的参数选择一个尚未分配的 IP 地址，分配给该客户端。DHCP 服务器用 Offer 报文将这个信息传达给客户端；
3. 客户端收集收到的 Offer 报文。由于网络中可能存在多于一个 DHCP 服务器，因此客户端可能收集到多个 Offer 报文。客户端从这些报文中选择一个，并向网络中广播 Request 报文，表示选择这个 DHCP 服务器发送的配置；
4. DHCP 服务器收到 Request 报文后，首先判断该客户端是否选择本服务器分配的地址：如果不是，则在本服务器上解除对那个 IP 地址的占用；否则则再次确认分配的地址有效，并向客户端发送 Ack 报文，表示确认配置有效，Ack 报文中包括配置的有效时间。如果 DHCP 发现分配的地址无效，则返回 Nak 报文；
5. 客户端收到 Ack 报文后，确认服务器分配的地址有效，即确认服务器分配的地址未被其它客户端占用，则完成网络配置，同时记录配置的有效时间，出于简化的目的，我们不考虑被占用的情况。若客户端收到 Nak 报文，则从步骤 1 重新开始；
6. 客户端在到达配置的有效时间前，再次向 DHCP 服务器发送 Request 报文，表示希望延长 IP 地址的有效期。DHCP 服务器按照步骤 4 确定是否延长，客户端按照步骤 5 处理后续的配置；

在本题目中，你需要理解 DHCP 协议的工作过程，并按照题目的要求实现一个简单的 DHCP 服务器。

报文格式

为了便于实现，我们简化地规定 DHCP 数据报文的格式如下：

<发送主机> <接收主机> <报文类型> <IP 地址> <过期时刻>

DHCP 数据报文的各个部分由空格分隔，其各个部分的定义如下：

• 发送主机：是发送报文的主机名，主机名是由小写字母、数字组成的字符串，唯一地表示了一个主机；
• 接收主机：当有特定的接收主机时，是接收报文的主机名；当没有特定的接收主机时，为一个星号（*）；
• 报文类型：是三个大写字母，取值如下：
  • DIS：表示 Discover 报文；
  • OFR：表示 Offer 报文；
  • REQ：表示 Request 报文；
  • ACK：表示 Ack 报文；
  • NAK：表示 Nak 报文；
• IP 地址，是一个非负整数：
  • 对于 Discover 报文，该部分在发送的时候为 0，在接收的时候忽略；
  • 对于其它报文，为正整数，表示一个 IP 地址；
• 过期时刻，是一个非负整数：
  • 对于 Offer、Ack 报文，是一个正整数，表示服务器授予客户端的 IP 地址的过期时刻；
  • 对于 Discover、Request 报文，若为正整数，表示客户端期望服务器授予的过期时刻；
  • 对于其它报文，该部分在发送的时候为 0，在接收的时候忽略。

例如下列都是合法的 DHCP 数据报文：

a * DIS 0 0
d a ACK 50 1000

服务器配置

为了 DHCP 服务器能够正确分配 IP 地址，DHCP 需要接受如下配置：

• 地址池大小 N𝑁：表示能够分配给客户端的 IP 地址的数目，且能分配的 IP 地址是 1,2,…,N1,2,…,𝑁；
• 默认过期时间 Tdef𝑇𝑑𝑒𝑓：表示分配给客户端的 IP 地址的默认的过期时间长度；
• 过期时间的上限和下限 Tmax𝑇𝑚𝑎𝑥、Tmin𝑇𝑚𝑖𝑛：表示分配给客户端的 IP 地址的最长过期时间长度和最短过期时间长度，客户端不能请求比这个更长或更短的过期时间；
• 本机名称 H𝐻：表示运行 DHCP 服务器的主机名。

分配策略

当客户端请求 IP 地址时，首先检查此前是否给该客户端分配过 IP 地址，且该 IP 地址在此后没有被分配给其它客户端。

如果是这样的情况，则直接将 IP 地址分配给它，否则，总是分配给它最小的尚未占用过的那个 IP 地址。

如果这样的地址不存在，则分配给它最小的此时未被占用的那个 IP 地址。

如果这样的地址也不存在，说明地址池已经分配完毕，因此拒绝分配地址。

实现细节

在 DHCP 启动时，首先初始化 IP 地址池，将所有地址设置状态为未分配，占用者为空，并清零过期时刻。

其中地址的状态有未分配、待分配、占用、过期四种。

处于未分配状态的 IP 地址没有占用者，而其余三种状态的 IP 地址均有一名占用者。

处于待分配和占用状态的 IP 地址拥有一个大于零的过期时刻。

在到达该过期时刻时，若该地址的状态是待分配，则该地址的状态会自动变为未分配，且占用者清空，过期时刻清零；否则该地址的状态会由占用自动变为过期，且过期时刻清零。

处于未分配和过期状态的 IP 地址过期时刻为零，即没有过期时刻。

对于收到的报文，设其收到的时刻为 t𝑡。

处理细节如下：

1. 判断接收主机是否为本机，或者为 *，若不是，则判断类型是否为 Request，若不是，则不处理；
2. 若类型不是 Discover、Request 之一，则不处理；
3. 若接收主机为 *，但类型不是 Discover，或接收主机是本机，但类型是 Discover，则不处理。

对于 Discover 报文，按照下述方法处理：

1. 检查是否有占用者为发送主机的 IP 地址：
   • 若有，则选取该 IP 地址；
   • 若没有，则选取最小的状态为未分配的 IP 地址；
   • 若没有，则选取最小的状态为过期的 IP 地址；
   • 若没有，则不处理该报文，处理结束；
2. 将该 IP 地址状态设置为待分配，占用者设置为发送主机；
3. 若报文中过期时刻为 0 ，则设置过期时刻为 t+Tdef𝑡+𝑇𝑑𝑒𝑓；否则根据报文中的过期时刻和收到报文的时刻计算过期时间，判断是否超过上下限：若没有超过，则设置过期时刻为报文中的过期时刻；否则则根据超限情况设置为允许的最早或最晚的过期时刻；
4. 向发送主机发送 Offer 报文，其中，IP 地址为选定的 IP 地址，过期时刻为所设定的过期时刻。

对于 Request 报文，按照下述方法处理：

1. 检查接收主机是否为本机：
   • 若不是，则找到占用者为发送主机的所有 IP 地址，对于其中状态为待分配的，将其状态设置为未分配，并清空其占用者，清零其过期时刻，处理结束；
2. 检查报文中的 IP 地址是否在地址池内，且其占用者为发送主机，若不是，则向发送主机发送 Nak 报文，处理结束；
3. 无论该 IP 地址的状态为何，将该 IP 地址的状态设置为占用；
4. 与 Discover 报文相同的方法，设置 IP 地址的过期时刻；
5. 向发送主机发送 Ack 报文。

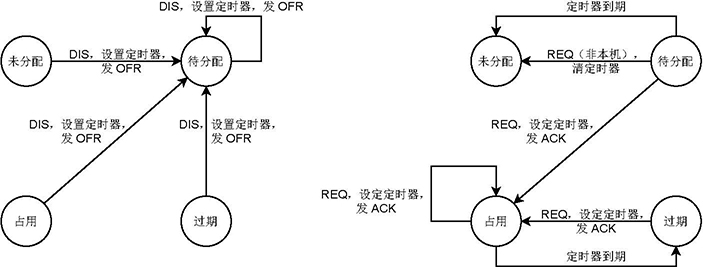
上述处理过程中，地址池中地址的状态的变化可以概括为如下图所示的状态转移图。

为了简洁，该图中没有涵盖需要回复 Nak 报文的情况。

输入格式

输入的第一行包含用空格分隔的四个正整数和一个字符串，分别是：N𝑁、Tdef𝑇𝑑𝑒𝑓、Tmax𝑇𝑚𝑎𝑥、Tmin𝑇𝑚𝑖𝑛 和 H𝐻，保证 Tmin≤Tdef≤Tmax𝑇𝑚𝑖𝑛≤𝑇𝑑𝑒𝑓≤𝑇𝑚𝑎𝑥。

输入的第二行是一个正整数 n𝑛，表示收到了 n𝑛 个报文。

输入接下来有 n𝑛 行，第 (i+2)(𝑖+2) 行有空格分隔的正整数 ti𝑡𝑖 和约定格式的报文 Pi𝑃𝑖。表示收到的第 i𝑖 个报文是在 ti𝑡𝑖 时刻收到的，报文内容是 Pi𝑃𝑖。保证 ti<ti+1𝑡𝑖<𝑡𝑖+1。

输出格式

输出有若干行，每行是一个约定格式的报文。依次输出 DHCP 服务器发送的报文。

数据范围

对于 20%20% 的数据，有 N≤200𝑁≤200，且 n≤N𝑛≤𝑁，且输入仅含 Discover 报文，且 t<Tmin𝑡<𝑇𝑚𝑖𝑛；
对于 50%50% 的数据，有 N≤200𝑁≤200，且 n≤N𝑛≤𝑁，且 t<Tmin𝑡<𝑇𝑚𝑖𝑛，且报文的接收主机或为本机，或为 *；
对于 70%70% 的数据，有 N≤1000𝑁≤1000，且 n≤N𝑛≤𝑁，且报文的接收主机或为本机，或为 *；
对于 100%100% 的数据，有 N≤10000𝑁≤10000，且 n≤10000𝑛≤10000，主机名的长度不超过 2020，且 t,Tmin,Tdefault,Tmax≤109𝑡,𝑇𝑚𝑖𝑛,𝑇𝑑𝑒𝑓𝑎𝑢𝑙𝑡,𝑇𝑚𝑎𝑥≤109，输入的报文格式符合题目要求，且数字不超过 109109。

输入样例1：

4 5 10 5 dhcp
16
1 a * DIS 0 0
2 a dhcp REQ 1 0
3 b a DIS 0 0
4 b * DIS 3 0
5 b * REQ 2 12
6 b dhcp REQ 2 12
7 c * DIS 0 11
8 c dhcp REQ 3 11
9 d * DIS 0 0
10 d dhcp REQ 4 20
11 a dhcp REQ 1 20
12 c dhcp REQ 3 20
13 e * DIS 0 0
14 e dhcp REQ 2 0
15 b dhcp REQ 2 25
16 b * DIS 0 0

输出样例1：

dhcp a OFR 1 6
dhcp a ACK 1 7
dhcp b OFR 2 9
dhcp b ACK 2 12
dhcp c OFR 3 12
dhcp c ACK 3 13
dhcp d OFR 4 14
dhcp d ACK 4 20
dhcp a ACK 1 20
dhcp c ACK 3 20
dhcp e OFR 2 18
dhcp e ACK 2 19
dhcp b NAK 2 0

样例1解释

输入第一行，分别设置了 DHCP 的相关参数，并收到了 1616 个报文。

第 11 个报文和第 22 个报文是客户端 a𝑎 正常请求地址，服务器为其分配了地址 11，相应地设置了过期时刻是 77（即当前时刻 22 加上默认过期时间 55）。

第 33 个报文不符合 Discover 报文的要求，不做任何处理。

第 44 个报文 b𝑏 发送的 Discover 报文虽然有 IP 地址 33，但是按照处理规则，这个字段被忽略，因此服务器返回 Offer 报文，过期时刻是 99。

第 55 个报文中，Request 报文不符合接收主机是 DHCP 服务器本机的要求，因此不做任何处理。

第 66 个报文是 b𝑏 发送的 Request 报文，其中设置了过期时刻是 1212，没有超过最长过期时间，因此返回的 Ack 报文中过期时刻也是 1212。

第 77 个报文中，过期时刻 1111 小于最短过期时间，因此返回的过期时刻是 1212。虽然此时为 a𝑎 分配的地址 11 过期，但是由于还有状态为未分配的地址 33，因此为 c𝑐 分配地址 33。

第 88 个报文同理，为 c𝑐 分配的地址过期时刻是 1313。

第 9、109、10 两个报文中，为 d𝑑 分配了地址 44，过期时刻是 2020。

第 1111 个报文中，a𝑎 请求重新获取此前为其分配的地址 11，虽然为其分配的地址过期，但是由于尚未分配给其它客户端，因此 DHCP 服务器可以直接为其重新分配该地址，并重新设置过期时刻为 2020。

第 1212 个报文中，c𝑐 请求延长其地址的过期时刻为 2020。DHCP 正常向其回复 Ack 报文。

第 13、1413、14 个报文中，e𝑒 试图请求地址。此时地址池中已经没有处于“未分配”状态的地址了，但是有此前分配给 b𝑏 的地址 22 的状态是“过期”，因此把该地址重新分配给 e𝑒。

第 1515 个报文中，b𝑏 试图重新获取此前为其分配的地址 22，但是此时该地址已经被分配给 e𝑒，因此返回 Nak 报文。

第 1616 个报文中，b𝑏 试图重新请求分配一个 IP 地址，但是此时地址池中已经没有可用的地址了，因此忽略该请求。

输入样例2：

4 70 100 50 dhcp
6
5 a * OFR 2 100
10 b * DIS 0 70
15 b dhcp2 REQ 4 60
20 c * DIS 0 70
70 d * DIS 0 120
75 d dhcp REQ 1 125

输出样例2：

dhcp b OFR 1 70
dhcp c OFR 1 70
dhcp d OFR 1 120
dhcp d ACK 1 125

样例2解释

在本样例中，DHCP 服务器一共收到了 66 个报文，处理情况如下：

第 11 个报文不是 DHCP 服务器需要处理的报文，因此不回复任何报文。

第 22 个报文中，b𝑏 请求分配 IP 地址，因此 DHCP 服务器将地址 11 分配给 b𝑏，此时，地址 11 进入待分配状态，DHCP 服务器向 b𝑏 发送 Offer 报文。

第 33 个报文中，b𝑏 发送的 REQ 报文是发给非本服务器的，因此需要将地址池中所有拥有者是 b𝑏 的待分配状态的地址修改为未分配。

第 44 个报文中，c𝑐 请求分配 IP 地址。由于地址 11 此时是未分配状态，因此将该地址分配给它，向它发送 Offer 报文，地址 11 进入待分配状态。

第 5、65、6 个报文中，d𝑑 请求分配 IP 地址。注意到在收到第 55 个报文时，已经是时刻 7070，地址 11 的过期时刻已到，它的状态已经被修改为了未分配，因此 DHCP 服务器仍然将地址 11 分配给 d𝑑。

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 10010;

int n, m, t_def, t_max, t_min;
string h;
struct IP
{
    int state;  // 0：未分配，1：待分配，2：占用，3：过期
    int t;  // 过期时间
    string owner;
}ip[N];

void update_ips_state(int tc)
{
    for (int i = 1; i <= n; i ++ )
        if (ip[i].t && ip[i].t <= tc)
        {
            if (ip[i].state == 1)
            {
                ip[i].state = 0;
                ip[i].owner = "";
                ip[i].t = 0;
            }
            else
            {
                ip[i].state = 3;
                ip[i].t = 0;
            }
        }
}

int get_ip_by_owner(string client)
{
    for (int i = 1; i <= n; i ++ )
        if (ip[i].owner == client)
            return i;
    return 0;
}

int get_ip_by_state(int state)
{
    for (int i = 1; i <= n; i ++ )
        if (ip[i].state == state)
            return i;
    return 0;
}

int main()
{
    cin >> n >> t_def >> t_max >> t_min >> h;
    cin >> m;

    while (m -- )
    {
        int tc;
        string client, server, type;
        int id, te;
        cin >> tc >> client >> server >> type >> id >> te;
        if (server != h && server != "*")
        {
            if (type != "REQ") continue;
        }
        if (type != "DIS" && type != "REQ") continue;
        if (server == "*" && type != "DIS" || server == h && type == "DIS") continue;

        update_ips_state(tc);
        if (type == "DIS")
        {
            int k = get_ip_by_owner(client);
            if (!k) k = get_ip_by_state(0);
            if (!k) k = get_ip_by_state(3);
            if (!k) continue;
            ip[k].state = 1, ip[k].owner = client;
            if (!te) ip[k].t = tc + t_def;
            else
            {
                int t = te - tc;
                t = max(t, t_min), t = min(t, t_max);
                ip[k].t = tc + t;
            }
            cout << h << ' ' << client << ' ' << "OFR" << ' ' << k << ' ' << ip[k].t << endl;
        }
        else
        {
            if (server != h)
            {
                for (int i = 1; i <= n; i ++ )
                    if (ip[i].owner == client && ip[i].state == 1)
                    {
                        ip[i].state = 0;
                        ip[i].owner = "";
                        ip[i].t = 0;
                    }
                continue;
            }
            if (!(id >= 1 && id <= n && ip[id].owner == client))
                cout << h << ' ' << client << ' ' << "NAK" << ' ' << id << ' ' << 0 << endl;
            else
            {
                ip[id].state = 2;
                if (!te) ip[id].t = tc + t_def;
                else
                {
                    int t = te - tc;
                    t = max(t, t_min), t = min(t, t_max);
                    ip[id].t = tc + t;
                }
                cout << h << ' ' << client << ' ' << "ACK" << ' ' << id << ' ' << ip[id].t << endl;
            }
        }
    }

    return 0;
}

作者：yxc
链接：https://www.acwing.com/activity/content/code/content/1155703/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

4010. 箱根山岳险天下 - AcWing题库

今年，京都大学也想派出长跑队参加箱根驿传，田径部的长跑教练组织起一批预备役运动员，并开展了严苛的训练。

京都大学的训练一共会持续 m𝑚 天，在训练过程中正式队员的名单可能发生变化。

简单起见，我们约定在且仅在第 t(1≤t≤m)𝑡(1≤𝑡≤𝑚) 天结束时，会有以下三种事件之一发生：

1. 有一个学生跑 10km10km 的速度达到了正式队员要求，教练将其作为最后一名纳入正式队员的名单中，这个学生的强度为 x𝑥；或者速度排名在最后一位的正式队员，由于速度过慢，而被从正式队员的名单中淘汰。
   • 在训练过程中，我们假定队员的速度的相对排名不会发生变化，与强度无关。
   • 严苛的教练制订了残酷的规则：被淘汰的学生虽然依然会跟大家一起训练，但将不能再次加入本年度参加箱根驿传的正式队员的名单中。
2. 由于近日的训练，第 s𝑠 天结束时速度排名为 l𝑙 至 r𝑟 的选手的强度有了变化，变为此前的 y𝑦 倍。
3. 教练在深夜想知道近日训练的效果，于是他统计了第 s𝑠 天结束时速度排名为 l𝑙 至 r𝑟 的选手目前（即第 t𝑡 天结束时）强度的和。由于这个结果可能很大，方便起见我们只考虑其模 p𝑝 的值。

出于学生们的隐私考虑，事件日志有可能会被加密。

输入格式

第一行为三个用空格隔开的整数 m𝑚，p𝑝 和 T𝑇。

如果 T=0𝑇=0，事件 11 中 x=x′𝑥=𝑥′，事件 22 中 y=y′𝑦=𝑦′；

如果 T=1𝑇=1，表示事件日志被加密了，事件 11 中 x=x′⊕A𝑥=𝑥′⊕𝐴，事件 22 中 y=y′⊕A𝑦=𝑦′⊕𝐴，其中 ⊕⊕ 为按位异或运算，A𝐴 为此前最后一次事件 33 所统计出的结果。如果此前没有事件 33 发生，则 A=0𝐴=0。

接下来 m𝑚 行，第 t𝑡 行表示在第 t𝑡 天结束时发生的事件：

• 1 x'：表示事件 11 发生。若 x>0𝑥>0，表示有一个强度为 x𝑥 的学生作为最后一名纳入正式队员的名单；若 x=0𝑥=0，表示排名在最后的正式队员被从名单中淘汰。保证有 0≤x′<2300≤𝑥′<230。
• 2 s l r y'：表示事件 22 发生。保证有 1≤s≤t1≤𝑠≤𝑡，1≤l≤r≤n1≤𝑙≤𝑟≤𝑛，0≤y′<2300≤𝑦′<230，其中 n𝑛 为在第 s𝑠 天结束时正式队员的人数。
• 3 s l r：表示事件 33 发生。保证有 1≤s≤t1≤𝑠≤𝑡，1≤l≤r≤n1≤𝑙≤𝑟≤𝑛，其中 n𝑛 为在第 s𝑠 天结束时正式队员的人数。

输出格式

对于每一个事件 33，输出一行一个数字，为其所统计出的结果。

数据范围

1≤m≤3×105,2≤p<230,mode∈{0,1}1≤𝑚≤3×105,2≤𝑝<230,𝑚𝑜𝑑𝑒∈{0,1}

测试点	特殊性质	mode𝑚𝑜𝑑𝑒
11	m≤5000𝑚≤5000	11
22	事件 11 中 x>0𝑥>0	11
33	没有事件 22	11
44	事件 11 中 x𝑥 在 0,10,1 中随机选取	00
55	r−l≤10𝑟−𝑙≤10	00
66	r−l≤10𝑟−𝑙≤10	11
7,87,8	无	00
9,109,10	无	11

输入样例1：

8 10 0
1 7
1 3
1 0
1 4
2 4 1 2 2
3 2 1 2
2 1 1 1 3
3 6 1 2

输出样例1：

7
0

样例1解释

第 11 天结束时，有一个强度为 77 的学生被列为正式队员，我们不妨称他为小津。此时正式队员名单依次为：小津。

第 22 天结束时，有一个强度为 33 的学生被列为正式队员，我们不妨称他为城崎。此时正式队员名单依次为：小津、城崎。

第 33 天结束时，城崎被淘汰了。此时正式队员名单为：小津。

第 44 天结束时，有一个强度为 44 的学生被列为正式队员，我们不妨称他为樋口清太郎。此时正式队员名单依次为：小津、樋口清太郎。

第 55 天结束时，由于近日的训练，第 44 天正式队员名单中第 11 至 22 个人——即小津和樋口清太郎——的强度乘了 22，所以，小津的强度达到了 1414，樋口清太郎的强度达到了 88。

第 66 天结束时，教练统计了第 22 天正式队员名单中第 11 至 22 个人——即小津和城崎——当前的强度，小津的强度为 1414，城崎的强度为 33，故统计结果为 1717，模 p𝑝 的值为 77。

第 77 天结束时，由于近日的训练，第 11 天正式队员名单中的第 11 个人——即小津——的强度乘了 33，所以，小津的强度达到了 4242。

第 88 天结束时，教练统计了第 66 天正式队员名单中第 11 至 22 个人——即小津和樋口清太郎——当前的强度，小津的强度为 4242，樋口清太郎的强度为 88，故统计结果为 5050，模 p𝑝 的值为 00。

输入样例2：

200 307854322 1
1 304192542
1 261749745
1 227234660
1 258761107
1 71490397
1 72584186
1 172113773
1 170623186
1 109308637
1 108383253
1 221430535
1 184520171
1 12820964
1 64943840
1 271383631
1 103269159
1 12002213
1 141551258
1 200255671
1 303679342
1 177153246
1 242934504
1 192722694
1 81041418
1 129449540
1 208869479
1 193883084
1 47265951
1 14844237
1 204331401
1 120715260
1 183356222
1 151061115
1 97645108
1 95770509
1 10891614
1 136365751
1 277592250
1 244161106
1 74405936
1 140365146
1 22587603
1 172441554
1 300179553
1 235367849
1 75467014
1 291045594
1 220071302
1 26967280
1 279868778
1 109902396
1 286509675
1 275417760
1 74253569
1 57318310
1 147462465
1 89999340
1 17784677
1 245244350
1 138709004
1 214478013
1 134244031
1 298548097
1 17276277
1 183802269
1 22366514
1 275904549
1 142230969
1 116156399
1 63581175
1 136336228
1 214860504
1 72329372
1 204231581
1 78276583
1 277642488
1 81760292
1 7831561
1 134535873
1 42237141
1 165620849
1 286362129
1 87388726
1 288617590
1 97675237
1 113222505
1 292912
1 98092392
1 257549905
1 180583994
1 244157382
1 117371320
1 304810612
1 148813285
1 150599985
1 229632823
1 246806551
1 297736161
1 66536628
1 70165839
1 31086027
1 0
1 46984478
1 0
3 13 2 11
1 134407869
1 134407869
2 73 7 31 130418473
1 134407869
1 62804642
1 134407869
1 134407869
3 28 12 21
1 173819539
3 93 34 83
3 68 5 38
1 95422722
2 85 54 85 89788932
2 28 2 25 251954506
1 185543612
1 34466375
1 185543612
2 28 2 13 51844756
3 43 22 33
3 97 5 87
1 53569742
1 83590412
1 53569742
2 1 1 1 131620724
2 128 5 72 41971821
1 53569742
1 197197823
1 333156690
3 59 48 50
1 224641252
1 24037560
3 54 26 40
2 91 7 37 58105019
2 59 4 50 254285874
3 112 17 63
3 103 53 54
3 3 1 3
3 4 4 4
2 121 68 76 258392700
2 88 55 59 10180251
2 110 45 76 125533148
1 160394017
1 170735200
3 51 18 34
3 136 43 64
1 49346652
1 114223193
3 62 17 26
3 57 8 40
1 278848254
1 278848254
1 411603847
1 278848254
1 278848254
1 278848254
2 112 70 79 437553006
2 120 4 89 428224488
3 53 50 51
2 109 36 81 205513848
3 81 31 46
3 78 45 64
2 107 19 28 8661353
3 36 21 33
2 28 4 28 227981470
2 42 18 29 7067955
1 1536382
1 214941299
1 176373062
2 172 26 74 241772251
1 21368911
2 61 50 61 37266210
3 84 30 48
3 31 8 24
1 297156062
1 328205831
2 175 57 77 408989526
1 528105214
2 30 4 24 416690156
3 9 4 8
1 31664726
3 144 40 67
1 276474902
2 115 56 72 15951722
2 187 6 50 38653155
1 17582098
1 276474902
1 415944350
3 34 1 24
1 204461450
2 136 1 59 92444637
3 79 7 79
3 22 2 17
1 284506459
2 166 78 86 22058413
1 30931926

输出样例2：

134407869
184056088
13293385
185543612
34566045
53569742
224641252
2971977
10689074
196073568
220349662
170735200
273278086
25664733
155812556
278848254
238098134
256392602
172981220
1536382
57033232
297156062
31664726
276474902
204461450
168966052
30931926

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

#define x first
#define y second

using namespace std;

typedef long long LL;
typedef pair<int, int> PII;

const int N = 300010;

int n, p, T;

struct Node
{
    int s[2], p, v;
    int rev;
    int sum, mul;
}tr[N];
int stk[N], idx;  // 栈
int fa[N], dep[N];
int A;
vector<PII> level[N];

void pushrev(int x)
{
    swap(tr[x].s[0], tr[x].s[1]);
    tr[x].rev ^= 1;
}

void pushup(int x)
{
    tr[x].sum = tr[x].v;
    int l = tr[x].s[0], r = tr[x].s[1];
    if (l) tr[x].sum = (tr[x].sum + tr[l].sum) % p;
    if (r) tr[x].sum += tr[r].sum;
    tr[x].sum %= p;
}

void pushdown(int x)
{
    if (tr[x].rev)
    {
        pushrev(tr[x].s[0]), pushrev(tr[x].s[1]);
        tr[x].rev = 0;
    }

    auto &root = tr[x], &left = tr[tr[x].s[0]], &right = tr[tr[x].s[1]];
    if (root.mul != 1)
    {
        LL mul = root.mul;
        left.v = left.v * mul % p;
        left.sum = left.sum * mul % p;
        left.mul = left.mul * mul % p;

        right.v = right.v * mul % p;
        right.sum = right.sum * mul % p;
        right.mul = right.mul * mul % p;

        root.mul = 1;
    }
}

bool isroot(int x)  // 判断x是否为原树的根节点
{
    return tr[tr[x].p].s[0] != x && tr[tr[x].p].s[1] != x;
}

void rotate(int x)  // splay的旋转操作
{
    int y = tr[x].p, z = tr[y].p;
    int k = tr[y].s[1] == x;
    if (!isroot(y)) tr[z].s[tr[z].s[1] == y] = x;
    tr[x].p = z;
    tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
    tr[x].s[k ^ 1] = y, tr[y].p = x;
    pushup(y), pushup(x);
}

void splay(int x)  // splay操作
{
    int top = 0, r = x;
    stk[ ++ top] = r;
    while (!isroot(r)) stk[ ++ top] = r = tr[r].p;
    while (top) pushdown(stk[top -- ]);
    while (!isroot(x))
    {
        int y = tr[x].p, z = tr[y].p;
        if (!isroot(y))
            if ((tr[y].s[1] == x) ^ (tr[z].s[1] == y)) rotate(x);
            else rotate(y);
        rotate(x);
    }
}

void access(int x)  // 建立一条从根到x的路径，同时将x变成splay的根节点
{
    int z = x;
    for (int y = 0; x; y = x, x = tr[x].p)
    {
        splay(x);
        tr[x].s[1] = y, pushup(x);
    }
    splay(z);
}

void makeroot(int x)  // 将x变成原树的根节点
{
    access(x);
    pushrev(x);
}

int findroot(int x)  // 找到x所在原树的根节点, 再将原树的根节点旋转到splay的根节点
{
    access(x);
    while (tr[x].s[0]) pushdown(x), x = tr[x].s[0];
    splay(x);
    return x;
}

void split(int x, int y)  // 给x和y之间的路径建立一个splay，其根节点是y
{
    makeroot(x);
    access(y);
}

void link(int x, int y)  // 如果x和y不连通，则加入一条x和y之间的边
{
    makeroot(x);
    if (findroot(y) != x) tr[x].p = y;
}

int find(int x, int y)
{
    int l = 0, r = level[x].size() - 1;
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (level[x][mid].x <= y) l = mid;
        else r = mid - 1;
    }
    return level[x][r].y;
}

int main()
{
    scanf("%d%d%d", &n, &p, &T);

    int cur = 0;
    for (int i = 1; i <= n; i ++ )
    {
        int op;
        scanf("%d", &op);
        if (op == 1)
        {
            int x;
            scanf("%d", &x);
            x ^= A;
            if (x > 0)
            {
                ++ idx;
                tr[idx].sum = tr[idx].v = x;
                tr[idx].mul = 1;
                if (cur) link(cur, idx);
                fa[idx] = cur, dep[idx] = dep[cur] + 1;
                cur = idx;
                level[dep[cur]].push_back({i, cur});
            }
            else
            {
                cur = fa[cur];
            }
        }
        else if (op == 2)
        {
            int s, l, r, y;
            scanf("%d%d%d%d", &s, &l, &r, &y);
            y ^= A;
            l = find(l, s), r = find(r, s);
            split(l, r);
            tr[r].v = tr[r].v * (LL)y % p;
            tr[r].sum = tr[r].sum * (LL)y % p;
            tr[r].mul = tr[r].mul * (LL)y % p;
        }
        else
        {
            int s, l, r;
            scanf("%d%d%d", &s, &l, &r);
            l = find(l, s), r = find(r, s);
            split(l, r);

            printf("%d\n", tr[r].sum);
            if (T) A = tr[r].sum;
        }
    }

    return 0;
}

作者：yxc
链接：https://www.acwing.com/activity/content/code/content/2120840/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

这次先看两题，上面两道和角色授权是一类的

3280. 推荐系统

•    题目
•    提交记录
•    讨论
•    题解
•    视频讲解

某电商有编号为 00 到 m−1𝑚−1 的 m𝑚 类商品，包括家电、汽车、电动车、面包、化妆品等。

对于每个 app 新用户，每类商品初始有编号不同的 n𝑛 个商品，包括各个商家、品牌、供应商等。

在任何时刻，同类的任意两个商品的编号各不相同，不同类的任意两个商品的编号可能相同。

app 会给每个商品打分。

初始时，各类商品的编号和得分都相同。

在用户使用 app 时，会产生有效信息，包括喜欢、不喜欢等。

app 会根据这些信息，在某类商品增加或删除商品。

app 每次会推荐一部分商品给用户看。

一个简单的想法是，选出各类所有商品中得分最大的若干商品。

该方法虽然简单，但是如果某类商品可能得分特别高，这种简单想法就无法保证推荐商品的多样性。

因此，app 查询得分最大的若干商品，同时限制各类商品个数不能超过一个阈值。

将上述过程抽象成 33 种操作：操作 1、2、31、2、3，分别对应增加、删除、查询操作：

• 1 type commodity score 表示在 type 类商品中增加编号为 commodity 的商品，该商品分数为 score。
• 2 type commodity 表示在 type 类商品中删除编号为 commodity 的商品。

• 3 K k_0 k_1 ... k_{m-1} 表示在各类所有商品中选出不超过 K𝐾 个（不一定要达到 K𝐾 个〉得分最大的商品，同时第 i(0≤i<m)𝑖(0≤𝑖<𝑚) 类商品的个数不超过 ki𝑘𝑖。在查询时，如果第 a(0≤a<m)𝑎(0≤𝑎<𝑚) 类商品中编号为 b𝑏 的商品和第 A(0≤A<m)𝐴(0≤𝐴<𝑚) 类商品中编号为 B𝐵 的商品得分相同:

  1. 当 a=A𝑎=𝐴 时，选取编号为 min(b,B)𝑚𝑖𝑛(𝑏,𝐵) 的商品;
  2. 当 a≠A𝑎≠𝐴 时，选取第 min(a,A)𝑚𝑖𝑛(𝑎,𝐴) 类商品。

输入格式

输入的第一行包含两个正整数 m𝑚 和 n𝑛。

接下来 n𝑛 行，每行两个正整数 id 和 score。第 1+j(1≤j≤n)1+𝑗(1≤𝑗≤𝑛) 行表示所有 m𝑚 类商品的第 j𝑗 个商品的编号和得分。

接下来一行包含一个正整数 opnum𝑜𝑝𝑛𝑢𝑚，表示操作总数。其中，查询操作一共有 opask𝑜𝑝𝑎𝑠𝑘 个。

接下来 opnum𝑜𝑝𝑛𝑢𝑚 行，每行若干个正整数，格式对应 1 type commodity score、2 type commodity、3 K k_0 k_1 ... k_{m-1}。

输出格式

输出共 opask×m𝑜𝑝𝑎𝑠𝑘×𝑚 行，对应 opask𝑜𝑝𝑎𝑠𝑘 个查询操作。第 r×m+c,0≤r<opask,1≤c≤m𝑟×𝑚+𝑐,0≤𝑟<𝑜𝑝𝑎𝑠𝑘,1≤𝑐≤𝑚 行表示，在第 r𝑟 个查询操作中，第 c𝑐 类商品选出的商品编号，同类商品输出时先输出分值大的，分值相同时先输出标号小的。如果 r𝑟 个查询操作中，第 c𝑐 类商品没有选出任何商品，则该行输出 −1−1。

数据范围

输入样例：

2 3
1 3
2 2
3 1
8
3 100 1 1
1 0 4 3
1 0 5 1
3 10 2 2
3 10 1 1
2 0 1
3 2 1 1
3 1 1 1

输出样例：

1
1
1 4
1 2
1
1
4
1
4
-1

#include <iostream>
#include <cstring>
#include <algorithm>
#include <set>
#include <vector>
#include <unordered_map>

#define x first
#define y second

using namespace std;

typedef pair<int, int> PII;
const int N = 55;

int m, n;
set<PII> g[N];
unordered_map<int, int> f[N];
int sum[N], cnt[N];
set<PII>::reverse_iterator it[N];
vector<int> ans[N];

int main()
{
    scanf("%d%d", &m, &n);
    for (int i = 1; i <= n; i ++ )
    {
        int id, score;
        scanf("%d%d", &id, &score);
        for (int j = 0; j < m; j ++ )
        {
            f[j][id] = score;
            g[j].insert({score, -id});
        }
    }

    int Q;
    scanf("%d", &Q);
    while (Q -- )
    {
        int t;
        scanf("%d", &t);
        if (t == 1)
        {
            int type, id, score;
            scanf("%d%d%d", &type, &id, &score);
            f[type][id] = score;
            g[type].insert({score, -id});
        }
        else if (t == 2)
        {
            int type, id;
            scanf("%d%d", &type, &id);
            g[type].erase({f[type][id], -id});
            f[type].erase(id);
        }
        else
        {
            int tot;
            scanf("%d", &tot);
            for (int i = 0; i < m; i ++ )
            {
                scanf("%d", &sum[i]);
                it[i] = g[i].rbegin();
                cnt[i] = 0;
                ans[i].clear();
            }
            while (tot -- )
            {
                int k = -1;
                for (int i = 0; i < m; i ++ )
                    if (it[i] != g[i].rend() && cnt[i] < sum[i])
                        if (k == -1 || it[i]->x > it[k]->x)
                            k = i;
                if (k == -1) break;
                ans[k].push_back(-it[k]->y);
                cnt[k] ++ ;
                it[k] ++ ;
            }
            for (int i = 0; i < m; i ++ )
                if (ans[i].empty()) puts("-1");
                else
                {
                    for (auto x: ans[i])
                        printf("%d ", x);
                    puts("");
                }
        }
    }
    return 0;
}

作者：yxc
链接：https://www.acwing.com/activity/content/code/content/911199/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

4457. 计算资源调度器

•    题目
•    提交记录
•    讨论
•    题解
•    视频讲解

西西艾弗岛上兴建了一批数据中心，建设了云计算资源平台。

小 C𝐶 是主管西西艾弗云开发的工程师。

西西艾弗云中有大量的计算节点，每个计算节点都有唯一编号。

西西艾弗云分为多个可用区，每个计算节点位于一个特定的可用区。

一个可用区中可以有多个计算节点。

西西艾弗云中运行的计算任务分为不同的应用，每个计算任务都有一个应用与之对应，一个应用中可能包括多个计算任务。

每个计算任务由一个特定的计算节点执行，下文中计算任务“运行在某可用区上”意即“运行在某可用区的计算节点上”。

不同的计算任务对运行的计算节点的要求不尽相同。

有的计算任务需要在指定可用区上运行，有的计算任务要和其它应用的计算任务在同一个可用区上运行，还有的希望不要和某个应用的计算任务在同一个计算节点上运行。

对于一个计算任务，执行它的计算节点一旦选定便不再更改；在选定计算节点后，该任务对计算节点的要求就不再被考虑，即使新安排的计算任务使得此前已有的计算任务的要求被违反，也是合法的。

下图示意性地说明了可用区、计算节点、计算任务之间的关系，同时也说明了应用和计算任务的对应关系。

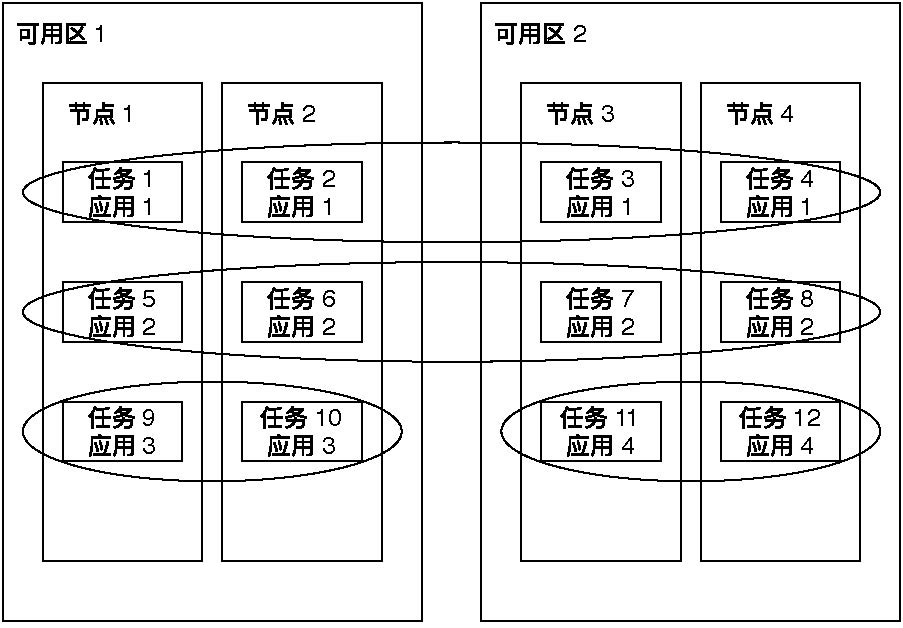
一开始，小 C𝐶 使用了电子表格程序来统计计算任务的分配情况。

随着云上的计算节点和计算任务的不断增多，小 C𝐶 被这些奇怪的要求搞得焦头烂额，有的时候还弄错了安排，让客户很不满意。

小 C𝐶 找到你，希望你能为他提供一个程序，能够输入要运行的计算任务和对节点的要求，结合西西艾弗云的现有计算节点信息，计算出计算任务应该被安排在哪个计算节点上。

计算任务对计算节点的要求十分复杂而且又不好描述，你对小 C𝐶 表示写程序这件事很为难。

于是，小 C𝐶 进行了调研，将这些需求进行了归纳整理，形成了下面这三种标准需求。

在提出需求时，必须从这三种标准需求中选取若干种，每种需求只能有一条。选取多种需求意味着要同时满足这些需求。

计算节点亲和性

计算任务必须在指定可用区上运行。

计算任务亲和性

计算任务必须和指定应用的计算任务在同一可用区上运行。
该要求对计算任务可以运行的可用区添加了限制。不考虑该任务本身，一个可用区若运行有指定应用的任务，则满足要求。

计算任务反亲和性

计算任务不能和指定应用的计算任务在同一个计算节点上运行。
该要求对计算任务可以运行的计算节点添加了限制。不考虑该任务本身，一个计算节点若运行有指定应用的任务，则不满足要求。
当要执行的计算任务多起来，计算任务反亲和性的要求可能很难满足。因此在添加计算任务反亲和性要求时，还要指定这个要求是“必须满足”还是“尽量满足”。

小 C𝐶 要求你按照如下方法来分配计算节点：按照计算任务的启动顺序，根据要求，依次为每个计算任务选择计算节点。

一旦选择了一个计算节点，就固定下来不再变动，并且在此后的选择中，不再考虑这个计算任务的要求。

对每个计算任务，选择计算节点的方法是：

过滤阶段

在这个阶段，先根据计算任务的要求，过滤出所有满足要求的计算节点。

如果不存在这样的计算节点，并且指定了计算任务反亲和性要求，并且计算任务反亲和性要求是尽量满足的，那么去掉计算任务反亲和性要求，再过滤一次。

如果还不存在，就认为该计算任务的要求无法满足，该计算任务无法分配。

排序阶段

在这个阶段，将过滤后的计算节点按照这个方法排序：

1. 选择此时运行计算任务数量最少的计算节点；
2. 选择编号最小的计算节点。

输入格式

输入的第一行包含两个由空格分隔的正整数 n𝑛 和 m𝑚，分别表示计算节点的数目和可用区的数目。计算节点从 11 到 n𝑛 编号，可用区从 11 到 m𝑚 编号；

输入的第二行包含 n𝑛 个由空格分隔的正整数 l1,l2,…li,…,ln𝑙1,𝑙2,…𝑙𝑖,…,𝑙𝑛，表示编号为 i𝑖 的计算节点位于编号为 li𝑙𝑖 的可用区。其中，0<li≤m0<𝑙𝑖≤𝑚；

输入的第三行包含一个正整数 g𝑔，表示计算任务的组数；

接下来的 g𝑔 行，每行包含六个由空格分隔的整数 fi𝑓𝑖、ai𝑎𝑖、nai𝑛𝑎𝑖、pai𝑝𝑎𝑖、paai𝑝𝑎𝑎𝑖、paari𝑝𝑎𝑎𝑟𝑖，表示依次启动的一组计算任务的信息，其中：

• fi𝑓𝑖：表示要接连启动 fi𝑓𝑖 个所属应用和要求相同的计算任务，其中 fi>0𝑓𝑖>0；
• ai𝑎𝑖：表示这 fi𝑓𝑖 个计算任务所属应用的编号，其中 0<ai≤Amax0<𝑎𝑖≤𝐴𝑚𝑎𝑥（Amax𝐴𝑚𝑎𝑥 代表最大应用编号）；
• nai𝑛𝑎𝑖：表示计算节点亲和性要求，其中 0≤nai≤m0≤𝑛𝑎𝑖≤𝑚。当 nai=0𝑛𝑎𝑖=0 时，表示没有计算节点亲和性要求；否则表示要运行在编号为 nai𝑛𝑎𝑖 的可用区内的计算节点上；
• pai𝑝𝑎𝑖：表示计算任务亲和性要求，其中 0≤pai≤Amax0≤𝑝𝑎𝑖≤𝐴𝑚𝑎𝑥。当 pai=0𝑝𝑎𝑖=0 时，表示没有计算任务亲和性要求；否则表示必须和编号为 pai𝑝𝑎𝑖 的应用的计算任务在同一个可用区运行；
• paai𝑝𝑎𝑎𝑖：表示计算任务反亲和性要求，其中 0≤paai≤Amax0≤𝑝𝑎𝑎𝑖≤𝐴𝑚𝑎𝑥。当 paai=0𝑝𝑎𝑎𝑖=0 时，表示没有计算任务反亲和性要求；否则表示不能和编号为 paai𝑝𝑎𝑎𝑖 的应用的计算任务在同一个计算节点上运行；
• paari𝑝𝑎𝑎𝑟𝑖：表示计算任务亲和性要求是必须满足还是尽量满足，当 paai=0𝑝𝑎𝑎𝑖=0 时，paari𝑝𝑎𝑎𝑟𝑖 也一定为 00；否则 paari=1𝑝𝑎𝑎𝑟𝑖=1 表示“必须满足”，paari=0𝑝𝑎𝑎𝑟𝑖=0 表示“尽量满足”。

计算任务按组输入实际上是一种简化的记法，启动一组 (fi,ai,nai,pai,paai,paari)(𝑓𝑖,𝑎𝑖,𝑛𝑎𝑖,𝑝𝑎𝑖,𝑝𝑎𝑎𝑖,𝑝𝑎𝑎𝑟𝑖) 和连续启动 fi𝑓𝑖 组 (1,ai,nai,pai,paai,paari)(1,𝑎𝑖,𝑛𝑎𝑖,𝑝𝑎𝑖,𝑝𝑎𝑎𝑖,𝑝𝑎𝑎𝑟𝑖) 并无不同。

输入格式

输出 g𝑔 行，每行有 fi𝑓𝑖 个整数，由空格分隔，分别表示每个计算任务被分配的计算节点的情况。若该计算任务没有被分配，则输出 00；否则输出被分配的计算节点的编号。

数据范围

全部测试数据保证 0<m≤n≤10000<𝑚≤𝑛≤1000，0<g≤∑gi=1fi≤20000<𝑔≤∑𝑖=1𝑔𝑓𝑖≤2000。

部分测试点的特殊性质详见下表

测试点	最大应用编号	计算节点亲和性	计算任务亲和性	计算任务反亲和性
1,21,2	A{max}=10𝐴{𝑚𝑎𝑥}=10	无要求（nai=0𝑛𝑎𝑖=0）	无要求（pai=0𝑝𝑎𝑖=0）	无要求（paai=0𝑝𝑎𝑎𝑖=0）
3,43,4	A{max}=109𝐴{𝑚𝑎𝑥}=109	无要求（nai=0𝑛𝑎𝑖=0）	无要求（pai=0𝑝𝑎𝑖=0）	无要求（paai=0𝑝𝑎𝑎𝑖=0）
5,6,75,6,7	A{max}=10𝐴{𝑚𝑎𝑥}=10	nai≥0𝑛𝑎𝑖≥0	无要求（pai=0𝑝𝑎𝑖=0）	无要求（paai=0𝑝𝑎𝑎𝑖=0）
8,9,108,9,10	A{max}=109𝐴{𝑚𝑎𝑥}=109	nai≥0𝑛𝑎𝑖≥0	无要求（pai=0𝑝𝑎𝑖=0）	无要求（paai=0𝑝𝑎𝑎𝑖=0）
11,12,1311,12,13	A{max}=10𝐴{𝑚𝑎𝑥}=10	nai≥0𝑛𝑎𝑖≥0	无要求（pai=0𝑝𝑎𝑖=0）	paai≥0𝑝𝑎𝑎𝑖≥0
14,15,1614,15,16	A{max}=109𝐴{𝑚𝑎𝑥}=109	nai≥0𝑛𝑎𝑖≥0	无要求（pai=0𝑝𝑎𝑖=0）	paai≥0𝑝𝑎𝑎𝑖≥0
17,1817,18	A{max}=10𝐴{𝑚𝑎𝑥}=10	nai≥0𝑛𝑎𝑖≥0	pai≥0𝑝𝑎𝑖≥0	paai≥0𝑝𝑎𝑎𝑖≥0
19,2019,20	A{max}=109𝐴{𝑚𝑎𝑥}=109	nai≥0𝑛𝑎𝑖≥0	pai≥0𝑝𝑎𝑖≥0	paai≥0𝑝𝑎𝑎𝑖≥0

输入样例：

10 4
1 1 1 1 1 2 2 2 2 2
6
2 1 4 1 2 1
6 1 1 0 1 1
1 2 2 0 0 0
6 1 2 0 2 1
5 2 2 0 1 0
11 3 0 1 3 0

输出样例：

0 0
1 2 3 4 5 0
6
7 8 9 10 7 8
6 6 6 6 6
1 2 3 4 5 9 10 7 8 6 1

样例解释

本输入中声明了十个计算节点，前五个位于可用区 11，后五个位于可用区 22。可用区 33 和 44 不包含任何计算节点。

对于第一组计算任务，由于它们声明了计算节点亲和性要求，但要求的可用区编号是 44，该可用区不包含计算节点，因此都不能满足。

对于第二组计算任务，要在可用区 11 中启动 66 份应用 11 的任务，并且要求了计算任务反亲和性。因此，前五份任务分别被安排在前五个节点上。对于第六份任务，由于它必须运行于可用区 11，所以能够安排的范围仅限于前五个节点。但是它还指定了强制的计算任务反亲和性，前五个节点上已经启动了属于应用 11 的计算任务，因此没有能够运行它的节点。

对于第三组计算任务，要在可用区 22 中启动 11 份应用 22 的任务，直接将其分配给节点 66。

对于第四组计算任务，要在可用区 22 中启动 66 份应用 11 的任务，并且要求了计算任务反亲和性，不能和应用 22 的计算任务分配在同一个节点上。因此，节点 66 不能用于分配，这六份任务只能分配在节点 7∼107∼10 上。按照题意，选取运行任务数最少的和编号最小的，因此依次分配 7、8、9、10、7、87、8、9、10、7、8。

对于第五组计算任务，要在可用区 22 中启动 55 份应用 22 的任务，并且要求了尽量满足的计算任务反亲和性，不能和应用 11 的计算任务分配在同一个节点上。此时，可用区 22 中的节点 66 上没有应用 11 的计算任务，因此这 55 份计算任务都会被分配到这个节点上。

对于第六组计算任务，要启动 1111 份应用 33 的任务，并且要求了尽量满足的计算任务反亲和性，不能和应用 33 的其它计算任务分配在同一个节点上，同时要求和应用 11 的计算任务位于同一个可用区。应用 11 位于两个可用区，因此全部 1010 个节点都可以用于分配。对于前 1010 份任务，按照题意，依次选取运行的任务数最少且编号最小的节点进行分配。对于第 1111 份任务，由于所有的节点上都运行有应用 33 的任务，因此没有节点符合它的反亲和性要求。又因为反亲和性要求是尽量满足的，因此可以忽略这一要求，将它安排在节点 11 上。

3299. 带配额的文件系统

•    题目
•    提交记录
•    讨论
•    题解
•    视频讲解

小 H𝐻 同学发现，他维护的存储系统经常出现有人用机器学习的训练数据把空间占满的问题，十分苦恼。

查找了一阵资料后，他想要在文件系统中开启配额限制，以便能够精确地限制大家在每个目录中最多能使用的空间。

文件系统概述

文件系统，是一种树形的文件组织和管理方式。

在文件系统中，文件是指用名字标识的文件系统能够管理的基本对象，分为普通文件和目录文件两种，目录文件可以被简称为目录。

目录中有一种特殊的目录被叫做根目录。

除了根目录外，其余的文件都有名字，称为文件名。

合法的文件名是一个由若干数字（[0−9][0−9]）、大小写字母（[A−Za−z][𝐴−𝑍𝑎−𝑧]）组成的非空字符串。

普通文件中含有一定量的数据，占用存储空间；目录不占用存储空间。

文件和目录之间存在含于关系。

上述概念满足下列性质：

1. 有且仅有一个根目录；
2. 对于除根目录以外的文件，都含于且恰好含于一个目录；
3. 含于同一目录的文件，它们的文件名互不相同；
4. 对于任意不是根目录的文件 f𝑓，若 f𝑓 不含于根目录，那么存在有限个目录 d1,d2,…,dn𝑑1,𝑑2,…,𝑑𝑛，使得 f𝑓 含于 d1𝑑1，d1𝑑1 含于 d2𝑑2，……，dn𝑑𝑛 含于根目录。

结合性质 44 和性质 22 可知，性质 44 中描述的有限多个目录，即诸 di𝑑𝑖，是唯一的。

再结合性质 33，我们即可通过从根目录开始的一系列目录的序列，来唯一地指代一个文件。

我们记任意不是根目录且不含于根目录的文件 f𝑓 的文件名是 Nf𝑁𝑓，那么 f𝑓 的路径是：‘/′+Ndn+‘/′+⋯+Nd1+‘/′+Nf‘/′+𝑁𝑑𝑛+‘/′+⋯+𝑁𝑑1+‘/′+𝑁𝑓，其中符号 ++ 表示字符串的连接；对于含于根目录的文件 f𝑓，它的路径是：‘/′+Nf‘/′+𝑁𝑓；根目录的路径是：‘/′‘/′。

不符合上述规定的路径都是非法的。

例如：/A/B 是合法路径，但 /A//B、/A/、A/、A/B 都不是合法路径。

若文件 f𝑓 含于目录 d𝑑，我们也称 f𝑓 是 d𝑑 的孩子文件。

d𝑑 是 f𝑓 的双亲目录。

我们称文件 f𝑓 是目录 d𝑑 的后代文件，如果满足：(1) f𝑓 是 d𝑑 的孩子文件，或(2)f𝑓 含于 d𝑑 的后代文件。

如图所示，该图中绘制的文件系统共有 88 个文件。

其中，方形表示目录文件，圆形表示普通文件，它们之间的箭头表示含于关系。

在表示文件的形状上的文字是其文件名；各个形状的左上方标记了序号，以便叙述。

在该文件系统中，文件 55 含于文件 22，文件 55 是文件 22 的孩子文件，文件 55 也是文件 22 的后代文件。

文件 88 是文件 22 的后代文件，但不是文件 22 的孩子文件。

文件 88 的路径是 /D1/D1/F2。

配额概述

配额是指对文件系统中所含普通文件的总大小的限制。

对于每个目录 d𝑑，都可以设定两个配额值：目录配额和后代配额。

我们称目录配额 LDd𝐿𝐷𝑑 是满足的，当且仅当 d𝑑 的孩子文件中，全部普通文件占用的存储空间之和不大于该配额值。

我们称后代配额 LRd𝐿𝑅𝑑 是满足的，当且仅当 d𝑑 的后代文件中，全部普通文件占用的存储空间之和不大于该配额值。

我们称文件系统的配额是满足的，当且仅当该文件系统中所有的配额都是满足的。

很显然，若文件系统中仅存在目录，不存在普通文件，那么该文件系统的配额一定是满足的。

随着配额和文件的创建，某个操作会使文件系统的配额由满足变为不满足，这样的操作会被拒绝。

例如：试图设定少于目前已有文件占用空间的配额值，或者试图创建超过配额值的文件。

在本题中，假定初始状态下，文件系统仅包含根目录。

你将会收到若干对文件系统的操作指令。

对于每条指令，你需要判断该指令能否执行成功，对于能执行成功的指令，在成功执行该指令后，文件系统将会被相应地修改。

对于不能执行成功的指令，文件系统将不会发生任何变化。

你需要处理的指令如下：

创建普通文件

创建普通文件指令的格式如下：

C <file path> <file size>

创建普通文件的指令有两个参数，是空格分隔的字符串和一个正整数，分别表示需要创建的普通文件的路径和文件的大小。

对于该指令，若路径所指的文件已经存在，且也是普通文件的，则替换这个文件；若路径所指文件已经存在，但是目录文件的，则该指令不能执行成功。

当路径中的任何目录不存在时，应当尝试创建这些目录；若要创建的目录文件与已有的同一双亲目录下的孩子文件中的普通文件名称重复，则该指令不能执行成功。

另外，还需要确定在该指令的执行是否会使该文件系统的配额变为不满足，如果会发生这样的情况，则认为该指令不能执行成功，反之则认为该指令能执行成功。

移除文件

移除文件指令的格式如下：

R <file path>

移除文件的指令有一个参数，是字符串，表示要移除的文件的路径。

若该路径所指的文件不存在，则不进行任何操作。

若该路径所指的文件是目录，则移除该目录及其所有后代文件。

在上述过程中被移除的目录（如果有）上设置的配额值也被移除。

该指令始终认为能执行成功。

设置配额值

Q <file path> <LD> <LR>

设置配额值的指令有三个参数，是空格分隔的字符串和两个非负整数，分别表示需要设置配额值的目录的路径、目录配额和后代配额。

该指令表示对所指的目录文件，分别设置目录配额和后代配额。

若路径所指的文件不存在，或者不是目录文件，则该指令执行不成功。

若在该目录上已经设置了配额，则将原配额值替换为指定的配额值。

特别地，若配额值为 00，则表示不对该项配额进行限制。

若在应用新的配额值后，该文件系统配额变为不满足，那么该指令执行不成功。

输入格式

输入的第一行包含一个正整数 n𝑛，表示需要处理的指令条数。

输入接下来会有 n𝑛 行，每一行一个指令。

指令的格式符合前述要求。

输入数据保证：对于所有指令，输入的路径是合法路径；对于创建普通文件和移除文件指令，输入的路径不指向根目录。

输出格式

输出共有 n𝑛 行，表示相应的操作指令是否执行成功。若成功执行，则输出字母 Y；否则输出 N。

数据范围

本题目各个测试点的数据规模如下：

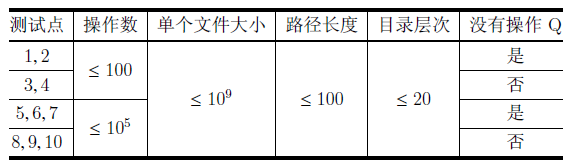
表格中，目录层次是指各指令中出现的路径中，/ 字符的数目。

所有输入的数字均不超过 10181018。

输入样例1：

10
C /A/B/1 1024
C /A/B/2 1024
C /A/B/1/3 1024
C /A 1024
R /A/B/1/3
Q / 0 1500
C /A/B/1 100
Q / 0 1500
R /A/B
Q / 0 1

输出样例1：

Y
Y
N
N
Y
N
Y
Y
Y
Y

样例1解释

输入总共有 1010 条指令。

其中前两条指令可以正常创建两个普通文件。

第三条指令试图创建 /A/B/1/3，但是 /A/B/1 已经存在，且不是目录，而是普通文件，不能再进一步创建孩子文件，因此执行不成功。

第四条指令试图创建 /A，但是 /A 已经存在，且是目录，因此执行不成功。

第五条指令试图删除 /A/B/1/3，由于该文件不存在，因此不对文件系统进行修改，但是仍然认为执行成功。

第六条指令试图在根目录增加后代配额限制，但此时，文件系统中的文件总大小是 20482048，因此该限制无法生效，执行不成功。

第七条指令试图创建文件 /A/B/1，由于 /A/B/1 已经存在，且是普通文件，因此该指令实际效果是将原有的该文件替换。

此时文件总大小是 11241124，因此第八条指令就可以执行成功了。

第九条指令递归删除了 /A/B 目录和它的所有后代文件。

此时文件系统中已经没有普通文件，因此第十条命令可以执行成功。

输入样例2：

9
Q /A/B 1030 2060
C /A/B/1 1024
C /A/C/1 1024
Q /A/B 1024 0
Q /A/C 0 1024
C /A/B/3 1024
C /A/B/D/3 1024
C /A/C/4 1024
C /A/C/D/4 1024

输出样例2：

N
Y
Y
Y
Y
N
Y
N
N

样例2解释

输入共有 99 条指令。

第一条指令试图为 /A/B 创建配额规则，然而该目录并不存在，因此执行不成功。

接下来的两条指令创建了两个普通文件。

再接下来的两条指令分别在目录 /A/B 和 /A/C 创建了两个配额规则。

其中前者是目录配额，后者是后代配额。

接下来的两条指令，创建了两个文件。

其中，/A/B/3 超出了在 /A/B 的目录配额，因此执行不成功；但 /A/B/D/3 不受目录配额限制，因此执行成功。

最后两条指令，创建了两个文件。

虽然在 /A/C 没有目录配额限制，但是无论是 /A/C 下的孩子文件还是后代文件，都受到后代配额的限制，因此两条指令执行都不成功。

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

#define x first
#define y second

using namespace std;

typedef long long LL;
typedef pair<int, int> PII;

const int N = 300010;

int n, p, T;

struct Node
{
    int s[2], p, v;
    int rev;
    int sum, mul;
}tr[N];
int stk[N], idx;  // 栈
int fa[N], dep[N];
int A;
vector<PII> level[N];

void pushrev(int x)
{
    swap(tr[x].s[0], tr[x].s[1]);
    tr[x].rev ^= 1;
}

void pushup(int x)
{
    tr[x].sum = tr[x].v;
    int l = tr[x].s[0], r = tr[x].s[1];
    if (l) tr[x].sum = (tr[x].sum + tr[l].sum) % p;
    if (r) tr[x].sum += tr[r].sum;
    tr[x].sum %= p;
}

void pushdown(int x)
{
    if (tr[x].rev)
    {
        pushrev(tr[x].s[0]), pushrev(tr[x].s[1]);
        tr[x].rev = 0;
    }

    auto &root = tr[x], &left = tr[tr[x].s[0]], &right = tr[tr[x].s[1]];
    if (root.mul != 1)
    {
        LL mul = root.mul;
        left.v = left.v * mul % p;
        left.sum = left.sum * mul % p;
        left.mul = left.mul * mul % p;

        right.v = right.v * mul % p;
        right.sum = right.sum * mul % p;
        right.mul = right.mul * mul % p;

        root.mul = 1;
    }
}

bool isroot(int x)  // 判断x是否为原树的根节点
{
    return tr[tr[x].p].s[0] != x && tr[tr[x].p].s[1] != x;
}

void rotate(int x)  // splay的旋转操作
{
    int y = tr[x].p, z = tr[y].p;
    int k = tr[y].s[1] == x;
    if (!isroot(y)) tr[z].s[tr[z].s[1] == y] = x;
    tr[x].p = z;
    tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
    tr[x].s[k ^ 1] = y, tr[y].p = x;
    pushup(y), pushup(x);
}

void splay(int x)  // splay操作
{
    int top = 0, r = x;
    stk[ ++ top] = r;
    while (!isroot(r)) stk[ ++ top] = r = tr[r].p;
    while (top) pushdown(stk[top -- ]);
    while (!isroot(x))
    {
        int y = tr[x].p, z = tr[y].p;
        if (!isroot(y))
            if ((tr[y].s[1] == x) ^ (tr[z].s[1] == y)) rotate(x);
            else rotate(y);
        rotate(x);
    }
}

void access(int x)  // 建立一条从根到x的路径，同时将x变成splay的根节点
{
    int z = x;
    for (int y = 0; x; y = x, x = tr[x].p)
    {
        splay(x);
        tr[x].s[1] = y, pushup(x);
    }
    splay(z);
}

void makeroot(int x)  // 将x变成原树的根节点
{
    access(x);
    pushrev(x);
}

int findroot(int x)  // 找到x所在原树的根节点, 再将原树的根节点旋转到splay的根节点
{
    access(x);
    while (tr[x].s[0]) pushdown(x), x = tr[x].s[0];
    splay(x);
    return x;
}

void split(int x, int y)  // 给x和y之间的路径建立一个splay，其根节点是y
{
    makeroot(x);
    access(y);
}

void link(int x, int y)  // 如果x和y不连通，则加入一条x和y之间的边
{
    makeroot(x);
    if (findroot(y) != x) tr[x].p = y;
}

int find(int x, int y)
{
    int l = 0, r = level[x].size() - 1;
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (level[x][mid].x <= y) l = mid;
        else r = mid - 1;
    }
    return level[x][r].y;
}

int main()
{
    scanf("%d%d%d", &n, &p, &T);

    int cur = 0;
    for (int i = 1; i <= n; i ++ )
    {
        int op;
        scanf("%d", &op);
        if (op == 1)
        {
            int x;
            scanf("%d", &x);
            x ^= A;
            if (x > 0)
            {
                ++ idx;
                tr[idx].sum = tr[idx].v = x;
                tr[idx].mul = 1;
                if (cur) link(cur, idx);
                fa[idx] = cur, dep[idx] = dep[cur] + 1;
                cur = idx;
                level[dep[cur]].push_back({i, cur});
            }
            else
            {
                cur = fa[cur];
            }
        }
        else if (op == 2)
        {
            int s, l, r, y;
            scanf("%d%d%d%d", &s, &l, &r, &y);
            y ^= A;
            l = find(l, s), r = find(r, s);
            split(l, r);
            tr[r].v = tr[r].v * (LL)y % p;
            tr[r].sum = tr[r].sum * (LL)y % p;
            tr[r].mul = tr[r].mul * (LL)y % p;
        }
        else
        {
            int s, l, r;
            scanf("%d%d%d", &s, &l, &r);
            l = find(l, s), r = find(r, s);
            split(l, r);

            printf("%d\n", tr[r].sum);
            if (T) A = tr[r].sum;
        }
    }

    return 0;
}

作者：yxc
链接：https://www.acwing.com/activity/content/code/content/2120840/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

3294. 点亮数字人生

•    题目
•    提交记录
•    讨论
•    题解
•    视频讲解

土豪大学的计算机系开了一门数字逻辑电路课，第一个实验叫做“点亮数字人生”，要用最基础的逻辑元件组装出实际可用的电路。

时间已经是深夜了，尽管实验箱上密密麻麻的连线已经拆装了好几遍，小君同学却依旧没能让她的电路正常工作。

你能帮助她模拟出电路的功能，成功点亮她的数字人生吗？

本题中，你需要实现一个简单的数字逻辑电路模拟器。

如果你已经有了此方面的基础，可以直接跳过本节。

在阅读时，也可以参照前两个样例的图示和解释，这有助于你更好地理解数字逻辑电路的工作原理。

数字逻辑电路是用来传输数字信号（也就是二进制信号）的电路。

一般来说，数字逻辑电路可以分为两大类，即组合逻辑（combinational logic）电路和时序逻辑（sequential logic）电路。

在本题中，我们仅关注组合逻辑电路。

这种电路仅由逻辑门（logical gate）构成。

一个逻辑门可以理解为一个多输入单输出的函数，输入端连接至少一个信号，而后经过一定的逻辑运算输出一个信号。

常见的逻辑门包括与（AND）、或（OR）、非（NOT）、异或（XOR）等，均与编程语言中的按位运算是对应的。

将一系列的逻辑门连接起来，就能构成具有特定功能的电路。

它的功能可能很简单（如一位二进制加法只需要一个异或门），也可能极其复杂（如除法）。

无论复杂程度，这类电路的特点是：它不维持任何的状态，任何时刻输出只与输入有关，随输入变化。

真实世界中的逻辑器件由于物理规律的限制，存在信号传播延时。

为了简单起见，本题中我们模拟的组合逻辑电路不考虑延时：一旦输入变化，输出立刻跟着变化。

考虑到组合逻辑电路的这一特性，设计时不能允许组合环路（combinational loop）的存在，即某逻辑门的输入经过了一系列器件之后又被连接到了自己的输入端。

真实世界中，这种做法将导致电路变得不稳定，甚至损坏元器件。

因此，你也需要探测可能的环路。

需要注意，环路的存在性与逻辑门的具体功能没有任何关系；只要连接关系上存在环路，电路就无法正常工作。

输入格式

输入数据包括若干个独立的问题，第一行一个整数 Q𝑄，满足 1≤Q≤Qmax1≤𝑄≤𝑄𝑚𝑎𝑥。

接下来依次是这 Q𝑄 个问题的输入，你需要对每个问题进行处理，并且按照顺序输出对应的答案。

每一个问题的输入在逻辑上可分为两部分。

第一部分定义了整个电路的结构，第二部分定义了输入和输出的要求。

实际上两部分之间没有分隔，顺序读入即可。

第一部分

第一行是两个空格分隔的整数 M,N𝑀,𝑁，分别表示了整个电路的输入和器件的数量，满足 1≤N≤Nmax1≤𝑁≤𝑁𝑚𝑎𝑥 并且 0≤M≤kmaxN0≤𝑀≤𝑘𝑚𝑎𝑥𝑁。其中 kmax𝑘𝑚𝑎𝑥 和 Nmax𝑁𝑚𝑎𝑥 都是与测试点编号有关的参数。

接下来 N𝑁 行，每行描述一个器件，编号从 11 开始递增，格式如下：

FUNC k L_1 L_2 ... L_k

其中 FUNC 代表具体的逻辑功能，k𝑘 表示输入的数量，后面跟着该器件的 k𝑘 个输入端描述 L𝐿，格式是以下二者之一：

• Im：表示第 m𝑚 个输入信号连接到此输入端，保证 1≤m≤M1≤𝑚≤𝑀；
• On：表示第 n𝑛 个器件的输出连接到此输入端，保证 1≤n≤N1≤𝑛≤𝑁。

所有可能的 FUNC 和允许的输入端数量如下表所述：

FUNC	最少输入数量	最多输入数量	功能描述
NOT	11	11	非
AND	22	k{max}𝑘{𝑚𝑎𝑥}	与
OR	22	k{max}𝑘{𝑚𝑎𝑥}	或
XOR	22	k{max}𝑘{𝑚𝑎𝑥}	异或
NAND	22	k{max}𝑘{𝑚𝑎𝑥}	与非（先全部与后取非）
NOR	22	k{max}𝑘{𝑚𝑎𝑥}	或非（先全部或后取非）

所有的器件均只有一个输出，但这个输出信号可以被用作多个器件的输入。

第二部分

第一行是一个整数 S𝑆，表示此电路需要运行 S𝑆 次。每次运行，都会给定一组输入，并检查部分器件的输出是否正确。S𝑆 满足 1≤S≤Smax1≤𝑆≤𝑆𝑚𝑎𝑥，其中 Smax𝑆𝑚𝑎𝑥 是一个与测试点编号有关的参数。

接下来的 S𝑆 行为输入描述，每一行的格式如下：

I_1 I_2 ... I_M

每行有 M𝑀 个可能为 00 或 11 的数字，表示各个输入信号（按编号排列）的状态。

接下来的 S𝑆 行为输出描述，每一行的格式如下：

s_i O_1 O_2 ... O_s

第一个整数 1≤si≤N(1≤i≤S)1≤𝑠𝑖≤𝑁(1≤𝑖≤𝑆) 表示需要输出的信号数量。后面共有 si𝑠𝑖 个在 11 到 N𝑁 之间的数字，表示在对应的输入下，组合逻辑完成计算后，需要输出结果的器件编号。

注意 O𝑂 序列不一定是递增的，即要求输出的器件可能以任意顺序出现。

输出格式

对于输入中的 Q𝑄 个问题，你需要按照输入顺序输出每一个问题的答案：

如果你检测到电路中存在组合环路，则请输出一行，内容是 LOOP，无需输出其他任何内容。

如果电路可以正常工作，则请输出 S𝑆 行，每一行包含 si𝑠𝑖 个用空格分隔的数字（可能为 00 或 11），依次表示“输出描述”中要求的各个器件的运算结果。

数据范围

输入样例1：

1
3 5
XOR 2 I1 I2
XOR 2 O1 I3
AND 2 O1 I3
AND 2 I1 I2
OR 2 O3 O4
4
0 1 1
1 0 1
1 1 1
0 0 0
2 5 2
2 5 2
2 5 2
2 5 2

输出样例1：

1 0
1 0
1 1
0 0

样例1解释

本样例只有一个问题，它定义的组合逻辑电路结构如下图所示。

其功能是一位全加器，即将三个信号相加，得到一个两位二进制数。

要求的器件 22 的输出是向更高位的进位信号，器件 55 的输出是本位的求和信号。

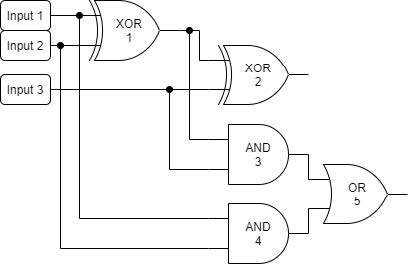
对于第一组输入 0 1 1，输出是 1 0；对于第二组输入 1 0 1，输出恰好依旧是 1 0（但电路内部状态不同）。

输入样例2：

1
2 6
NOR 2 O4 I2
AND 2 O4 O6
XOR 2 O5 O1
NOT 1 O6
NAND 2 O2 O2
AND 2 I1 O3
2
0 0
1 0
3 2 3 4
6 1 2 3 4 5 6

输出样例2：

LOOP

样例2解释

本样例也只有一个问题，它定义的组合逻辑电路结构如下图所示。

这是一个带组合环路的电路，因此无法正常工作。

特别地，其中最短的环路有以下三条：

• 6−2−5−3−66−2−5−3−6
• 4−1−3−6−44−1−3−6−4
• 2−5−3−6−2

3275. 消息传递接口

•    题目
•    提交记录
•    讨论
•    题解
•    视频讲解

消息传递接口（MPI）是一个并行计算的应用程序接口，常用于超级计算机、计算机集群等环境下的程序设计。

老师给了 T𝑇 份 MPI 的样例代码，每份代码都实现了 n𝑛 个进程通信。

这些进程标号从 00 到 n−1𝑛−1，每个进程会顺序执行自己的收发指令，如: S x，R x。

S x 表示向 x𝑥 号进程发送数据，R x 表示从 x𝑥 号进程接收数据。

每一对收发命令必须匹配执行才能生效，否则会“死锁”。

举个例子，x𝑥 号进程先执行发送命令 S y，y𝑦 号进程必须执行接送命令 R x，这一对命令才执行成功。

否则 x𝑥 号进程会一直等待 y𝑦 号进程执行对应的接收命令。

反之，若 y𝑦 号进程先执行接收命令 R x，则会一直等待 x𝑥 号进程执行发送命令 S y，若 x𝑥 号进程一直未执行发送命令 S y，则 y𝑦 号进程会一直等待 x𝑥 号进程执行对应的发送命令。

上述这样发送接收命令不匹配的情况都会造成整个程序出现“死锁”。

另外，x𝑥 号进程不会执行 S x 或 R x，即不会从自己的进程收发消息。

现在老师请你判断每份样例代码是否会出现“死锁”的情况。

每个进程的指令最少有 11 条，最多有 88 条，这些指令按顺序执行，即第一条执行完毕，才能执行第二条，依次到最后一条。

输入格式

输入第一行两个正整数 T,n𝑇,𝑛，表示有 T𝑇 份样例代码，实现了 n𝑛 个进程通信。

接下来有 T×n𝑇×𝑛 行，每行有若干个(1−81−8 个）字符串，相邻之间有一个空格隔开，表示相应进程的收发指令。不存在非法指令。对于第 2+i,0≤i<(T×n−1)2+𝑖,0≤𝑖<(𝑇×𝑛−1) 行，表示第 i÷n𝑖÷𝑛 (商）份代码的 imodn𝑖mod𝑛 (余数）号进程的收发指令。
(比如，S1 表示向 11 号进程发送消息，R1 表示从 11 号进程接收消息。细节请参考样例。)

输出格式

输出共 T𝑇 行，每行一个数字，表示对应样例代码是否出现“死锁”的情况。11 表示死锁，00 表示不死锁。

数据范围

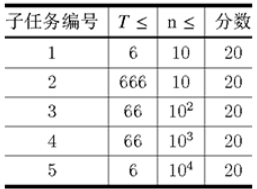
输入样例1：

3 2
R1 S1
S0 R0
R1 S1
R0 S0
R1 R1 R1 R1 S1 S1 S1 S1
S0 S0 S0 S0 R0 R0 R0 R0

输出样例1：

0
1
0

样例1解释

第 11 份代码中，(1) 00 号进程执行的 R1 和 11 号进程执行的 S0 成功执行;(2) 00 号进程执行的 S1 和 11 号进程执行的 R0 成功执行，所以未发生“死锁”，程序顺利运行。

第 11 份代码中，(1) 00 号进程执行的 R1 和 11 号进程执行的 R0 一直在等待发送命令，进入“死锁”状态。

输入样例2：

2 3
R1 S1
R2 S0 R0 S2
S1 R1
R1
R2 S0 R0
S1 R1

输出样例2：

0
1

样例2解释

第 11 份代码中，(1) 22 号进程执行的 S1 和 11 号进程执行的 R2 成功执行;(2) 00 号进程执行的 R1 和 11 号进程执行的S0 成功执行;(3) 00 号进程执行的 S1 和 11 号进程执行的 R0 成功执行;(4) 11 号进程执行的 S2 和 22 号进程执行的 R1 成功执行;所以未发生“死锁”，程序顺利运行。

第 11 份代码中，(1) 22 号进程执行的 S1 和 11 号进程执行的 R2 成功执行;(2) 00 号进程执行的 R1 和 11 号进程执行的 S0 成功执行;(3) 11 号进程执行的 R0 和 22 号进程执行的 R1 一直在等待发送命令;进入“死锁”状态。

3274. 损坏的RAID5

•    题目
•    提交记录
•    讨论
•    题解
•    视频讲解

独立硬盘冗余阵列（RAID,Redundant Array of Independent Disks）是一种现代常用的存储技术。

它以一定形式，将数据分散、冗余地存储在多个磁盘上，从而当部分磁盘不可用时，仍然能保证数据的完整性。

RAID 分为多种级别，提供了丰富的冗余性和性能的搭配方案选择。

本题中，我们主要研究一种十分常见的 RAID 级别——RAID5。

RAID5基本算法

RAID5 可以提供一块硬盘的冗余度，即阵列中至多允许有一块硬盘故障而不丢失数据。

RAID5 的基本原理是异或运算（⊕⊕）。考虑数

a1,a2,…,an𝑎1,𝑎2,…,𝑎𝑛

今令

p=a1⊕a2⊕⋯⊕an=⨁i=1nai𝑝=𝑎1⊕𝑎2⊕⋯⊕𝑎𝑛=⨁𝑖=1𝑛𝑎𝑖

易知

ak=p⊕⨁i=1..n,i≠kai𝑎𝑘=𝑝⊕⨁𝑖=1..𝑛,𝑖≠𝑘𝑎𝑖

上式意味着，在 p𝑝 与 a1…an𝑎1…𝑎𝑛 这 (n＋1)(𝑛＋1) 个数中，由任意 n𝑛 个可以推知其余的一个，这便是 RAID5 的基本原理。

由此，一种朴素的 (n＋1)(𝑛＋1) 块盘的存储方案是:将数据分块存放在前 n𝑛 块盘中，然后在第 (n＋1)(𝑛＋1) 块盘中存储前 n𝑛 块盘上相应位置处数据的异或结果。

这种方案的确可以实现 11 块硬盘的冗余度，但是很显然，如果所有的硬盘都没有发生故障，当读取数据时，最后一块盘完全不会被利用起来，在性能上较为浪费。

因此现行 RAID5 的存储方式采取了条带（stripe）化的方式，将被存储的数据均匀分布在所有磁盘上，从而提高了读写的性能。

硬盘及其组织

现代的硬盘可以被看作是一种能按块随机读写的持久化存储装置。

大多数硬盘每块的大小是 512512 字节或 40964096 字节，硬盘上所有的块，从 00 开始连续编号。

每次对硬盘的读写，都应该以块为单位，在读写时，传入被读写的块的编号，一次读写一整个块。

RAID 装置，可以将多个硬盘组织成一定的存储结构。

在上层软件看起来，被组织后的存储结构好像一整块大硬盘。

因此上层软件向 RAID 发送的读写指令里面的块的编号，应当被 RAID 装置进行适当地转换，反映到对具体某个硬盘或某几个硬盘的操作上。

条带化与数据布局

在 RAID5 中，一个重要的参数是条带大小。

条带是指连续、等大的数据块，是 RAID5 进行数据布局的基本单元。

例如，假设某硬盘有 10241024 个块，条带大小是 88 个块，那么这个硬盘一共被分为 128128 个条带，编号在 [0,8)[0,8) 的块在第一个条带上，编号 [8,16)[8,16) 的块在第二个条带上，依次类推。

一般地，如果将条带也从 00 开始编号，且条带大小为 s𝑠 个块，那么编号为 b𝑏 的块所在的条带编号是 ⌊bs⌋⌊𝑏𝑠⌋。

对于有 (n＋1)(𝑛＋1) 块硬盘的 RAID5 存储，我们利用每块硬盘上编号为 k𝑘 的条带，总共有 (n+1)(𝑛+1)块编号为 k𝑘 的条带，存储编号为 [kn,(k+1)n)[𝑘𝑛,(𝑘+1)𝑛) 的条带（共 n𝑛 个)。

这 n𝑛 个条带具体的存储方法是:先按一定规则，选中某个硬盘作为校验盘，存储这 n𝑛 个条带的异或和，然后再按一定顺序，将这 n𝑛 个条带存入其余的硬盘中。

选中校验盘的规则是：随着 k𝑘 递增，从最后一块盘开始，依次递减地选取校验盘，直到第一块盘为止，然后重新从最后一块盘开始。

存入数据条带的顺序是：从被选中的校验盘的下一块盘开始，依次存入数据条带，直到最后一块盘为止，然后从第一块盘开始，依次存入其余的数据条带，直到被选中的校验盘的上一块盘为止。

我们以 n=3𝑛=3 为例，示意性地给出条带的布局情况。

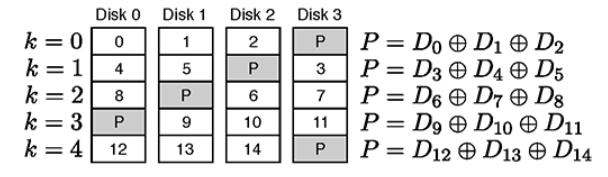
传说中，每个成功的运维背后，都坏着一打 RAID 阵列。

有一天，汉东省政法大学丁香学生公寓楼下的外卖又被偷了！

正在调取监控录像的关键时刻，汉东省政法大学监控中心的 RAID5 阵列发生了故障！

老师拿来了一摞同一个型号的“圆邪”牌硬盘，找到了你。

作为成功的运维，你能不能帮忙恢复里面的数据呢?

为了不辱使命，你立刻使用搜猫搜索得知，该型号硬盘的块大小是 44 字节。

当你正打算擅起袖子加油码代码的时候，电话响了，老师焦急的声音从听筒里传来:“哎呀呀，我好像把硬盘的顺序弄乱了.... ..”

输入格式

输入的第一行包含三个正整数 n(n≥2)、s𝑛(𝑛≥2)、𝑠 和 l𝑙，表示阵列中硬盘的数目、阵列的条带大小(单位:块）和现存的硬盘数目。

接下来的 l𝑙 行，每行包含由空格分开的一个非负整数和一个不含空格，长度相等且为 88 的整数倍的字符串。该整数为从零开始的这个硬盘的顺序号。该字符串仅包含数字 0∼90∼9 和大写字母 A∼F𝐴∼𝐹，每两个字符构成一个 1616 进制数字，表示一个字节的硬盘内容。输入硬盘集合保证：向该硬盘集合补充若干适当内容的硬盘，即可使它们恰好组成一个合法的、数据没有差错的 RAID5 阵列。输入数据保证：阵列的条带大小能整除每块硬盘的大小。

接下来的一行包含一个正整数 m𝑚，表示读取操作的数目。

接下来的 m𝑚 行，每行表示一个读取操作，包括一个非负整数 bi𝑏𝑖，表示要读取的块的编号。

输出格式

输出包含 m𝑚 行。

对于每一个读操作，产生一行输出。如果该读操作能进行，或能由现存的硬盘数据推算出来，则输出长度为 88 的字符串，该字符串仅包含数字 0∼90∼9 和大写字母 A∼F𝐴∼𝐹，每两个字符构成一个 1616 进制数字，表示读取到的数据块的内容。如果该读操作由于下列情形之一无法进行，则输出一个减号(-):

• 阵列不完整，且被读取的块所在的硬盘缺失，且该数据无法由现存的硬盘数据推算出来；
• 指定的块超出阵列总长度。

数据范围

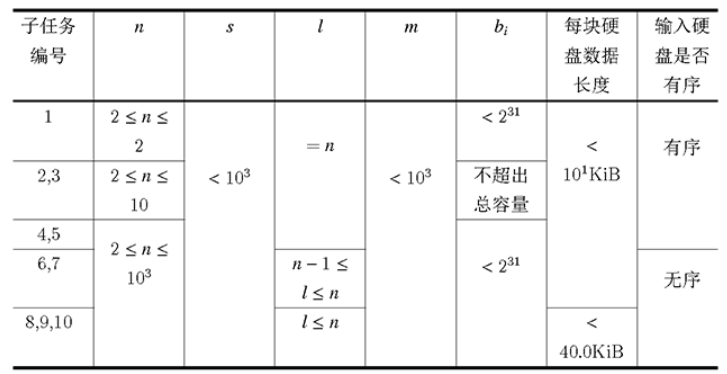
输入样例1：

2 1 2
0 000102030405060710111213141516172021222324252627
1 000102030405060710111213141516172021222324252627
2
0
1

输出样例1：

00010203
04050607

样例1解释

由题意，给出的 RAID5 阵列由两块盘组成，条带大小是 11 块(44 字节）长，并给出了两块盘的数据。

注意到当 RAID5 的阵列中只有两块盘时，有 p=a𝑝=𝑎，因此两块盘中数据是相同的，都是 RAID 阵列中的内容，因此可以任取一块盘进行读取操作。

输入样例2：

3 2 2
0 000102030405060710111213141516172021222324252627
1 A0A1A2A3A4A5A6A7B0B1B2B3B4B5B6B7C0C1C2C3C4C5C6C7
2
2
5

输出样例2：

A0A1A2A3
A0A0A0A0

样例2解释

由题意，给出的 RAID5 阵列由三块盘组成，条带大小是 22 块(88 字节）长，并给出了 00 号、11 号盘的数据，缺失 22 号盘，因此整个 RAID5 阵列的布局情况如图所示。

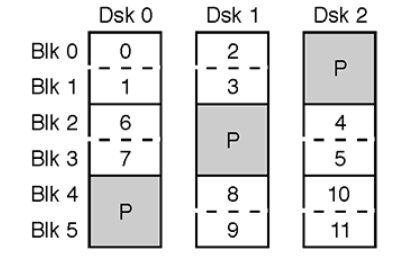
图中，用虚线隔开的长方形表示一个块，连续的两个长方形组成的正方形表示一个条带。

当读取编号为 22 的块时，该数据位于编号为 11 的盘的编号为 00 的块，因此结果是 A0A1A2A3𝐴0𝐴1𝐴2𝐴3;当读取编号为 55 的块时，该数据位于编号为 22 的盘的编号为 33 的块，该盘缺失，因此需要用其余两块盘相应位置处的数据进行异或运算得到 14151617⊕B4B5B6B7=A0A0A0A014151617⊕𝐵4𝐵5𝐵6𝐵7=𝐴0𝐴0𝐴0𝐴0。

3240. 压缩编码

•    题目
•    提交记录
•    讨论
•    题解
•    视频讲解

给定一段文字，已知单词 a1,a2,…,an𝑎1,𝑎2,…,𝑎𝑛 出现的频率分别 t1,t2,…,tn𝑡1,𝑡2,…,𝑡𝑛。

可以用 0101 串给这些单词编码，即将每个单词与一个 0101 串对应，使得任何一个单词的编码（对应的 0101 串）不是另一个单词编码的前缀，这种编码称为前缀码。

使用前缀码编码一段文字是指将这段文字中的每个单词依次对应到其编码。

一段文字经过前缀编码后的长度为：

L=a1𝐿=𝑎1 的编码长度 ×t1+a2×𝑡1+𝑎2 的编码长度 ×t2+…+an×𝑡2+…+𝑎𝑛 的编码长度 ×tn×𝑡𝑛。

定义一个前缀编码为字典序编码，指对于 1≤i<n1≤𝑖<𝑛，ai𝑎𝑖 的编码（对应的 0101 串）的字典序在 ai+1𝑎𝑖+1 编码之前，即 a1,a2,…,an𝑎1,𝑎2,…,𝑎𝑛 的编码是按字典序升序排列的。

例如，文字 E A E C D E B C C E C B D B E 中， 55 个单词 A、B、C、D、E𝐴、𝐵、𝐶、𝐷、𝐸 出现的频率分别为 1,3,4,2,51,3,4,2,5，则一种可行的编码方案是 A:000, B:001, C:01, D:10, E:11，对应的编码后的 0101 串为 1100011011011001010111010011000111，对应的长度 L𝐿 为 3×1+3×3+2×4+2×2+2×5=343×1+3×3+2×4+2×2+2×5=34。

在这个例子中，如果使用哈夫曼(Huffman)编码，对应的编码方案是 A:000, B:01, C:10, D:001, E:11，虽然最终文字编码后的总长度只有 3333，但是这个编码不满足字典序编码的性质，比如 C𝐶 的编码的字典序不在 D𝐷 的编码之前。

在这个例子中，有些人可能会想的另一个字典序编码是 A:000, B:001, C:010, D:011, E:1，编码后的文字长度为 3535。

请找出一个字典序编码，使得文字经过编码后的长度 L𝐿 最小。

在输出时，你只需要输出最小的长度 L𝐿，而不需要输出具体的方案。

在上面的例子中，最小的长度 L𝐿 为 3434。

输入格式

输入的第一行包含一个整数 n𝑛，表示单词的数量。

第二行包含 n𝑛 个整数，用空格分隔，分别表示 a1,a2,…,an𝑎1,𝑎2,…,𝑎𝑛 出现的频率，即 t1,t2,…,tn𝑡1,𝑡2,…,𝑡𝑛。

请注意 a1,a2,…,an𝑎1,𝑎2,…,𝑎𝑛 具体是什么单词并不影响本题的解，所以没有输入 a1,a2,…,an𝑎1,𝑎2,…,𝑎𝑛。

输出格式

输出一个整数，表示文字经过编码后的长度 L𝐿 的最小值。

数据范围

对于 30%30% 的评测用例，1<n≤10，1≤ti≤201<𝑛≤10，1≤𝑡𝑖≤20；
对于 60%60% 的评测用例，1<n≤100，1≤ti≤1001<𝑛≤100，1≤𝑡𝑖≤100；
对于 100%100% 的评测用例，1<n≤1000，1≤ti≤100001<𝑛≤1000，1≤𝑡𝑖≤10000。

输入样例：

5
1 3 4 2 5

输出样例：

34

样例解释

这个样例就是问题描述中的例子。如果你得到了 3535，说明你算得有问题，请自行检查自己的算法而不要怀疑是样例输出写错了。

3239. 权限查询

•    题目
•    提交记录
•    讨论
•    题解
•    视频讲解

授权 (authorization) 是各类业务系统不可缺少的组成部分，系统用户通过授权机制获得系统中各个模块的操作权限。

本题中的授权机制是这样设计的：每位用户具有若干角色，每种角色具有若干权限。

例如，用户 david 具有 manager 角色，manager 角色有 crm:2 权限，则用户 david 具有 crm:2 权限，也就是 crm 类权限的第 22 等级的权限。

具体地，用户名和角色名称都是由小写字母组成的字符串，长度不超过 3232。

权限分为分等级权限和不分等级权限两大类。

分等级权限由权限类名和权限等级构成，中间用冒号 : 分隔。

其中权限类名也是由小写字母组成的字符串，长度不超过 3232。

权限等级是一位数字，从 00 到 99，数字越大表示权限等级越高。

系统规定如果用户具有某类某一等级的权限，那么他也将自动具有该类更低等级的权限。

例如在上面的例子中，除 crm:2 外，用户 david 也具有 crm:1 和 crm:0 权限。

不分等级权限在描述权限时只有权限类名，没有权限等级（也没有用于分隔的冒号）。

给出系统中用户、角色和权限的描述信息，你的程序需要回答多个关于用户和权限的查询。

查询可分为以下几类：

• 不分等级权限的查询：如果权限本身是不分等级的，则查询时不指定等级，返回是否具有该权限；
• 分等级权限的带等级查询：如果权限本身分等级，查询也带等级，则返回是否具有该类的该等级权限；
• 分等级权限的不带等级查询：如果权限本身分等级，查询不带等级，则返回具有该类权限的最高等级；如果不具有该类的任何等级权限，则返回“否”。

输入格式

输入第一行是一个正整数 p𝑝，表示不同的权限类别的数量。

紧接着的 p𝑝 行被称为 P𝑃 段，每行一个字符串，描述各个权限。

对于分等级权限，格式为 <category>:<level>，其中 <category> 是权限类名，<level> 是该类权限的最高等级。

对于不分等级权限，字符串只包含权限类名。

接下来一行是一个正整数 r𝑟，表示不同的角色数量。

紧接着的 r𝑟 行被称为 R𝑅 段，每行描述一种角色，格式为

<role> <s> <privilege 1> <privilege 2> ... <privilege s>

其中 <role> 是角色名称，<s> 表示该角色具有多少种权限。

后面 <s> 个字符串描述该角色具有的权限，格式同 P𝑃 段。

接下来一行是一个正整数 u𝑢，表示用户数量。

紧接着的 u𝑢 行被称为 U𝑈 段，每行描述一个用户，格式为

<user> <t> <role 1> <role 2> ... <role t>

其中 <user> 是用户名，<t> 表示该用户具有多少种角色。

后面 <t> 个字符串描述该用户具有的角色。

接下来一行是一个正整数 q𝑞，表示权限查询的数量。

紧接着的 q𝑞 行被称为 Q𝑄 段，每行描述一个授权查询，格式为 <user> <privilege>，表示查询用户 <user> 是否具有 <privilege> 权限。

如果查询的权限是分等级权限，则查询中的 <privilege> 可指定等级，表示查询该用户是否具有该等级的权限；也可以不指定等级，表示查询该用户具有该权限的等级。

对于不分等级权限，只能查询该用户是否具有该权限，查询中不能指定等级。

输出格式

输出共 q𝑞 行，每行为 false、true，或者一个数字。

false 表示相应的用户不具有相应的权限，true 表示相应的用户具有相应的权限。

对于分等级权限的不带等级查询，如果具有权限，则结果是一个数字，表示该用户具有该权限的（最高）等级。

如果用户不存在，或者查询的权限没有定义，则应该返回 false。

数据范围

评测用例规模：

• 1≤p,r,u≤1001≤𝑝,𝑟,𝑢≤100
• 1≤q≤100001≤𝑞≤10000
• 每个用户具有的角色数不超过 1010，每种角色具有的权限种类不超过 1010

约定：

• 输入保证合法性，包括：
  　　1) 角色对应的权限列表（R𝑅 段）中的权限都是之前（P𝑃 段）出现过的，权限可以重复出现，如果带等级的权限重复出现，以等级最高的为准
  　　2) 用户对应的角色列表（U𝑈 段）中的角色都是之前（R𝑅 段）出现过的，如果多个角色都具有某一分等级权限，以等级最高的为准
  　　3) 查询（Q𝑄 段）中的用户名和权限类名不保证在之前（U𝑈 段和 P𝑃 段）出现过
• 前 20%20% 的评测用例只有一种角色
• 前 50%50% 的评测用例权限都是不分等级的，查询也都不带等级

额外声明：

• 保证没有两个不同的人或两个不同的角色或两个不同的权限出现重名的情况。
• 查询（Q𝑄 段）中的权限类名如果在之前（U𝑈 段和 P𝑃 段）出现过，则一定严格按照题面描述查询规定，为上述三类查询之一。（如果权限本身是不分等级的，则保证查询时不指定等级）

输入样例：

3
crm:2
git:3
game
4
hr 1 crm:2
it 3 crm:1 git:1 game
dev 2 git:3 game
qa 1 git:2
3
alice 1 hr
bob 2 it qa
charlie 1 dev
9
alice game
alice crm:2
alice git:0
bob git
bob poweroff
charlie game
charlie crm
charlie git:3
malice game

输出样例：

false
true
false
2
false
true
false
true
false

样例解释

样例输入描述的场景中，各个用户实际的权限如下：

在如今的互联网中，路由器扮演了一种很重要的角色，它可以高效而快速地处理 IP 数据包，根据其目的地址和路由规则，投向不同的下一个路由器。

自 Internet 建成以来，全球的 IPv4 路由条目稳步增长，根据 CIDR-Report 组织的统计，目前已经接近 8080 万条；IPv6 的路由条目也超过了 66 万条。

如此巨量的路由条目给骨干网上的路由器带来了很大的存储与处理压力。

为了节约路由器资源，很多路由器都会设法缩减路由表的大小。

在本题中，你需要实现一个通过合并前缀条目来缩减前缀列表的算法。

为了简便起见，我们暂时不考虑 IPv6 地址。

IP 地址及其表示

IP 地址是一个 3232 位无符号整数。

为了方便人类阅读，IP 地址可以被表示为点分十进制的形式: a3.a2.a1.a0𝑎3.𝑎2.𝑎1.𝑎0，其中诸 ai∈[0,256)𝑎𝑖∈[0,256)，是用十进制表示的不含前导零的整数。

a3.a2.a1.a0𝑎3.𝑎2.𝑎1.𝑎0 所表示的 IP 地址是 ∑k=03ak×256k∑𝑘=03𝑎𝑘×256𝑘。

例如 101.6.6.6101.6.6.6 表示的 IP 地址是十进制整数 16948935741694893574 或十六进制整数 0x650606060𝑥65060606。

下面示意性地列举一些合法和不合法的点分十进制表示的 IP 地址：

由上述定义易知，任何一个 IP 地址都有其点分十进制表示，并且任何合法的点分十进制的表示都唯一对应一个 IP 地址。

因此为了叙述方便，我们不再区分 IP 地址和它的点分十进制表示，你应当理解二者的等价性。

IP 前缀与前缀列表

IP 前缀是由一个 IP 地址和一个数字组成的有序二元组 <ip,len><𝑖𝑝,𝑙𝑒𝑛>，其中 len∈[0,32]𝑙𝑒𝑛∈[0,32] 称为前缀长度，且 ip𝑖𝑝 的低 (32−len)(32−𝑙𝑒𝑛) 二进制位为 00。

IP 前缀一般写作 a3.a2.a1.a0/len𝑎3.𝑎2.𝑎1.𝑎0/𝑙𝑒𝑛 的形式，其中 “a3.a2.a1.a0”“𝑎3.𝑎2.𝑎1.𝑎0” 是 ip𝑖𝑝 的点分十进制的表示，“len”“𝑙𝑒𝑛” 是十进制表示的数字，不含前导零，二者用斜线分开。

下面示意性地列举一些合法和不合法的 IP 前缀：

前缀列表是一个或多个 IP 前缀的无序可重复集合。

IP 地址和 IP 前缀的匹配关系

一个 IP 地址 ip𝑖𝑝 和一个 IP 前缀 <pref,len><𝑝𝑟𝑒𝑓,𝑙𝑒𝑛> 匹配，是指 ip𝑖𝑝 的高 len𝑙𝑒𝑛 二进制位与 pref𝑝𝑟𝑒𝑓 的高 len𝑙𝑒𝑛 二进制位相同。

一个 IP 地址和一个前缀列表匹配，是指这个 IP 地址至少和这个前缀列表中的一个 IP 前缀匹配。

我们定义一个 IP 前缀或前缀列表的匹配集为与这个 IP 前缀（列表）匹配的全体 IP 地址的集合。例如：

等价前缀列表

两个前缀列表等价，是指这两个前缀列表的匹配集相等。例如:

本题中，你将会得到一个前缀列表。

你的任务是，找到与之等价的包含 IP 前缀数目最少的前缀列表。

你的程序将会具有很高的实用价值，因此我们希望你的程序能够处理下面这几种简写形式的 IP 前缀：

输入格式

输入的第一行包含一个正整数 n𝑛，表示输入的前缀列表有 n𝑛 条 IP 前缀。

接下来的 n𝑛 行，每行一个合法的 IP 前缀。IP 前缀可能是标准型、省略后缀型、省略长度型中的任意一种。

输出格式

输出与输入前缀列表等价的包含 IP 前缀数目最少的前缀列表。

每个 IP 前缀占一行，用标准型输出。

输出的 IP 前缀按 IP 地址从小到大、前缀长度从小到大的顺序输出。

数据范围

1≤n≤1051≤𝑛≤105,

有些测试点具有特殊的性质：

测试点的输入数据规模:

输入样例1：

2
1
2

输出样例1：

1.0.0.0/8
2.0.0.0/8

输入样例2：

2
10/9
10.128/9

输出样例2：

10.0.0.0/8

输入样例3：

2
0/1
128/1

输出样例3：

0.0.0.0/0

提示

你可以用这样的办法计算包含 IP 前缀数目最少的等价前缀列表:

第一步:排序

将所有 IP 前缀进行排序，以其 IP 地址为第一关键字，以前缀长度为第二关键字从小到大排序，形成一个列表。

第二步:从小到大合并

从头到尾扫描该列表，依次考虑其相邻的两个元索 a,b𝑎,𝑏：如果 b𝑏 的匹配集是 a𝑎 的匹配集的子集，则将 b𝑏 从列表中移除。如果 b𝑏 后仍有元素 c𝑐，则此时 a𝑎 与 c𝑐 变为相邻的元素，你应当继续考虑这对新的相邻元素，直到 a𝑎 的下一个元素不能被移除。然后继续依次处理列表中接下来的相邻元素。可以证明，在此趟扫描结束之后，列表中不会存在任何两个元素 a,b𝑎,𝑏 使得 b𝑏 的匹配集是 a𝑎 的匹配集的子集。

第三步:同级合并

从头到尾扫描该列表，依次考虑其相邻的两个元素 a,b𝑎,𝑏：如果 a𝑎 与 b𝑏 的前缀长度相同，则设 a′𝑎′ 为一个新的 IP 前缀，其 IP 地址与 a𝑎 相同，而前缀长度比 a𝑎 少 11。如果 a′𝑎′ 合法且 a𝑎 的匹配集与 b𝑏 的匹配集的并集等于 a′𝑎′ 的匹配集，则将 a𝑎 与 b𝑏 从列表中移除，并将 a′𝑎′ 插入到列表中原来 a,b𝑎,𝑏 的位置。与上一步不同的是，如果 a′𝑎′ 之前存在元素，则接下来应当从 a𝑎 的前一个元素开始考虑；否则继续从 a′𝑎′ 开始考虑。

• 用户 alice 具有 crm:2 权限
• 用户 bob 具有 crm:1、git:2 和 game 权限
• 用户 charlie 具有 git:3 和 game 权限
• 用户 malice 未描述，因此不具有任何权限

• 3269. CIDR合并

•    题目
•    提交记录
•    讨论
•    题解
•    视频讲解
• 0.0.0.00.0.0.0 是合法的点分十进制表示；
• 1.255.255.2551.255.255.255 是合法的点分十进制表示；
• 101.6101.6 不是合法的点分十进制表示，因为它位数不足；
• 101.006.006.001101.006.006.001 不是合法的点分十进制表示，因为它的后三段整数都含有前导零；
• 101.6.123.456101.6.123.456 不是合法的点分十进制表示，因为它的最后一段数字超过了 255255。
• 0.0.0.0/00.0.0.0/0 是合法的 IP 前缀；
• 0.0.0.0/10.0.0.0/1 是合法的 IP 前缀；
• 1.2.0.0/161.2.0.0/16 是合法的 IP 前缀；
• 1.2.0.0/81.2.0.0/8 不是合法的 IP 前缀，因为 IP 地址 1.2.0.01.2.0.0 实际是十六进制数 0x010200000𝑥01020000，其低 2424 位不都是 00；
• 1.2.0.0/331.2.0.0/33 不是合法的 IP 前缀，因为它的前缀长度超过了 3232。
• 101.6.6.6101.6.6.6 与 101.6.6.0/24、101.6.6.0/23、101.6.0.0/16、101.0.0.0/8101.6.6.0/24、101.6.6.0/23、101.6.0.0/16、101.0.0.0/8 都匹配，但是与 101.6.0.0/24101.6.0.0/24 不匹配；
• 101.6.6.0/24101.6.6.0/24 的匹配集包含了从 101.6.6.0101.6.6.0 开始，到 101.6.6.255101.6.6.255 为止的所有 IP 地址；
• 101.6.6.128/25101.6.6.128/25 的匹配集包含了从 101.6.6.128101.6.6.128 开始，到 101.6.6.255101.6.6.255 为止的所有 IP 地址；
• 前缀列表 101.6.6.0/24，101.6.6.128/25101.6.6.0/24，101.6.6.128/25 的匹配集包含了从 101.6.6.0101.6.6.0 开始，到 101.6.6.255101.6.6.255 为止的所有 IP 地址；
• 101.6.6.6/32101.6.6.6/32 的匹配集中只有一个元素：101.6.6.6101.6.6.6；
• 0.0.0.0/00.0.0.0/0 的匹配集是全体 IP 地址。
• 前缀列表 101.6.6.0/24，101.6.6.128/25101.6.6.0/24，101.6.6.128/25 与前缀列表 101.6.6.0/24101.6.6.0/24 等价；
• 前缀列表 101.6.6.0/24，101.6.7.0/24101.6.6.0/24，101.6.7.0/24 与前缀列表 101.6.6.0/23101.6.6.0/23 等价。
• 标准型：形如 a3.a2.a1.a0/len𝑎3.𝑎2.𝑎1.𝑎0/𝑙𝑒𝑛。例如: 101.6.6.0/24101.6.6.0/24;
• 省略后缀型：在标准型的基础上，可以只写出 IP 地址的高位部分位段，没有写出的位段认为是 00；但 IP 地址至少要写一段。例如:
  • 101.6.6/23101.6.6/23 意为 101.6.6.0/23101.6.6.0/23；
  • 101/8101/8 意为 101.0.0.0/8101.0.0.0/8；
  • 1/321/32 意为 1.0.0.0/321.0.0.0/32；
• 省略长度型：当前缀长度是 8、16、248、16、24 或 3232 时，可以省略斜线和前缀长度不写，IP 地址只相应地写出前 1、2、31、2、3 或 44 段。例如:
  • 101.6.6.0101.6.6.0 意为 101.6.6.0/32101.6.6.0/32;
  • 101.6101.6 意为 101.6.0.0/16101.6.0.0/16；
  • 11 意为 1.0.0.0/81.0.0.0/8。
• 测试点 1,2,3,41,2,3,4 保证输出的 IP 前缀个数与输入的个数相同。这说明你不需要处理合并的情况，只需要完成排序的操作。
• 测试点 1,2,5,61,2,5,6 保证输入中只有标准型的 IP 前缀，即输入中没有省略的情况。
• 前 88 个测试点保证 n≤100𝑛≤100。
• 第 99 个测试点保证 n≤104𝑛≤104。
• 第 1010 个测试点保证 n≤105𝑛≤105。