一、贪心算法简介

常用方法：交换论证法、数学归纳法、反证法、分类讨论 

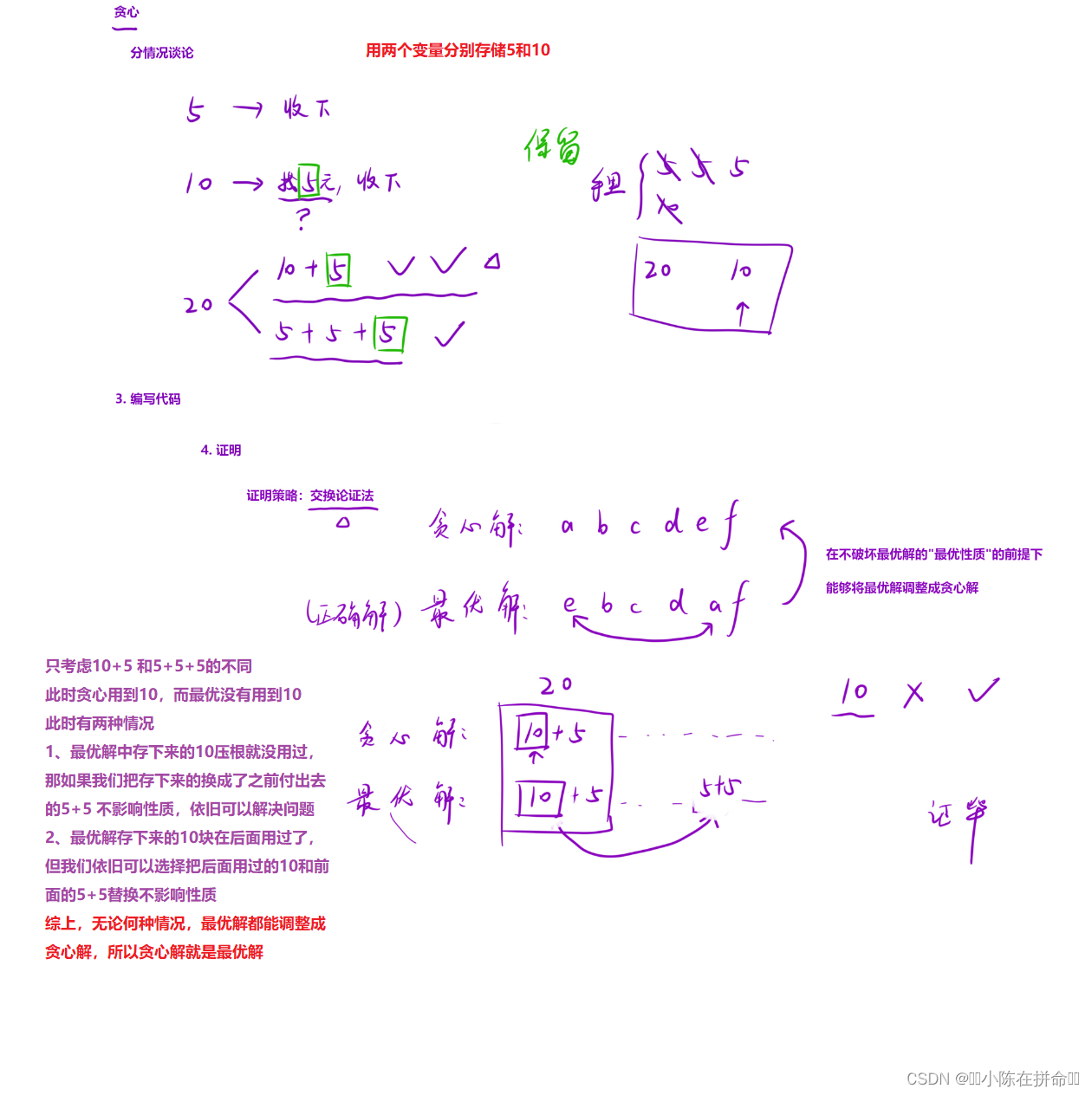
 二、柠檬水找零（交换论证法）

. - 力扣（LeetCode）

class Solution {
public:
    bool lemonadeChange(vector<int>& bills) {
         int five=0,ten=0;
         for(auto&e:bills)
            if(e==5) ++five;
            else if(e==10)
            {
                if(five==0) return false;
                --five,++ten;
            }
            else //贪心策略
            {
                if(five&&ten) --five,--ten;
                else if(five>=3) five-=3;
                else return false;
            }
         return true;
    }
    //交换论证法、数学归纳法和反证法常用的策略
};

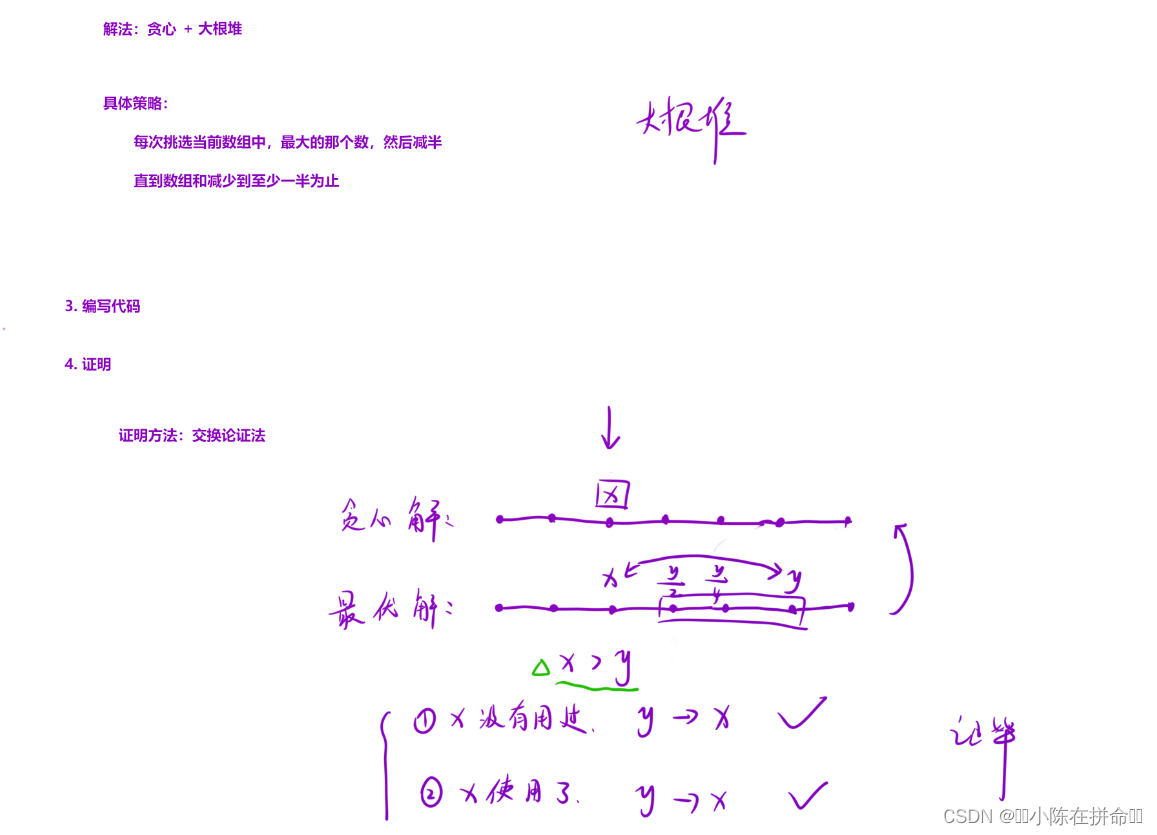
三、将数组减半的最小操作次数（交换论证法）

. - 力扣（LeetCode）

class Solution {
public:
    int halveArray(vector<int>& nums) {
        priority_queue<double> q(nums.begin(),nums.end());
        double sum=accumulate(nums.begin(),nums.end(),0.0);
        int ret=0;
        sum/=2.0;
        while(sum>0)
        {
            double t=q.top()/2.0;
            q.pop();
            sum-=t;
            q.push(t);
            ++ret;
        }
        return ret;
    }
};

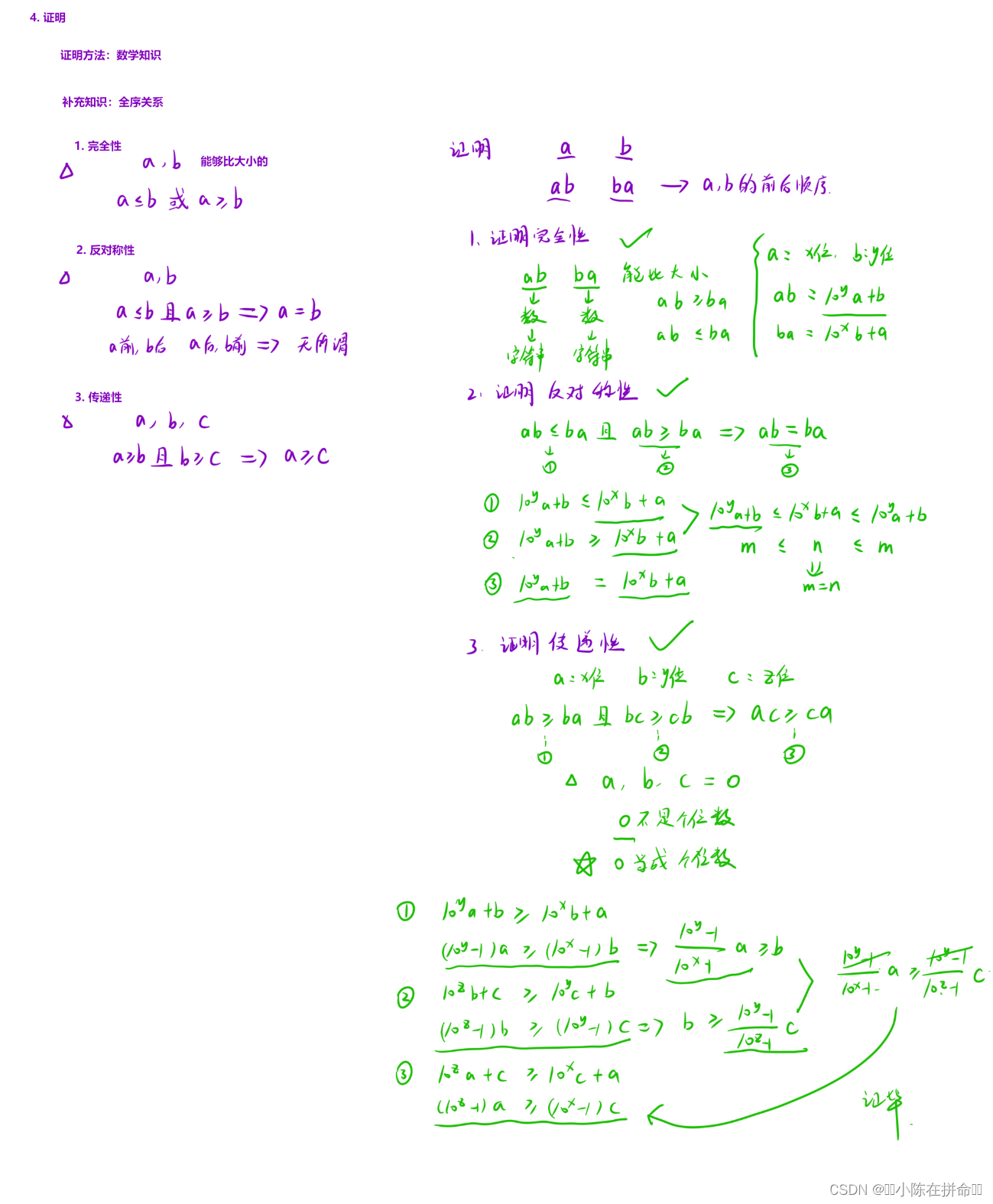
四、最大数（排序规则理解+全序性证明）

. - 力扣（LeetCode）

class Solution {
public:
    string largestNumber(vector<int>& nums) {
       //贪心策略 先转化成字符串 然后利用字典序排序
       vector<string> strs;
       strs.reserve(nums.size());//提前扩容 小优化
       for(auto&e:nums) strs.emplace_back(to_string(e));
       sort(strs.begin(),strs.end(),[](const string&s1,const string&s2)
       {
               return s1+s2>s2+s1;//大的在前面
       });
       //按顺序加入到ret中返回 
       string ret;
       for(auto&s:strs) ret+=s;
       //细节处理:前导0 除非都是0才会出现前导0  所以我们只需要当出现前导0的时候，返回"0"即可
       if(ret[0]=='0') return "0";
       return ret;
    }
    //全序关系  一个集合中任意选出两个元素 如果在你定义的比较规则下能够满足全序关系
                //我们就说这个集合是可以排序的
        //1、完全性 可以推测出他的大小关系（a>=b a<=b）
        //2、反对称性 a>=b&&b>=a  ——>a==b   a前和b前无所谓(唯一性)
        //3、传递性 a>=b  b>=c a>=c
};

五、摆动序列（反证法）

. - 力扣（LeetCode）

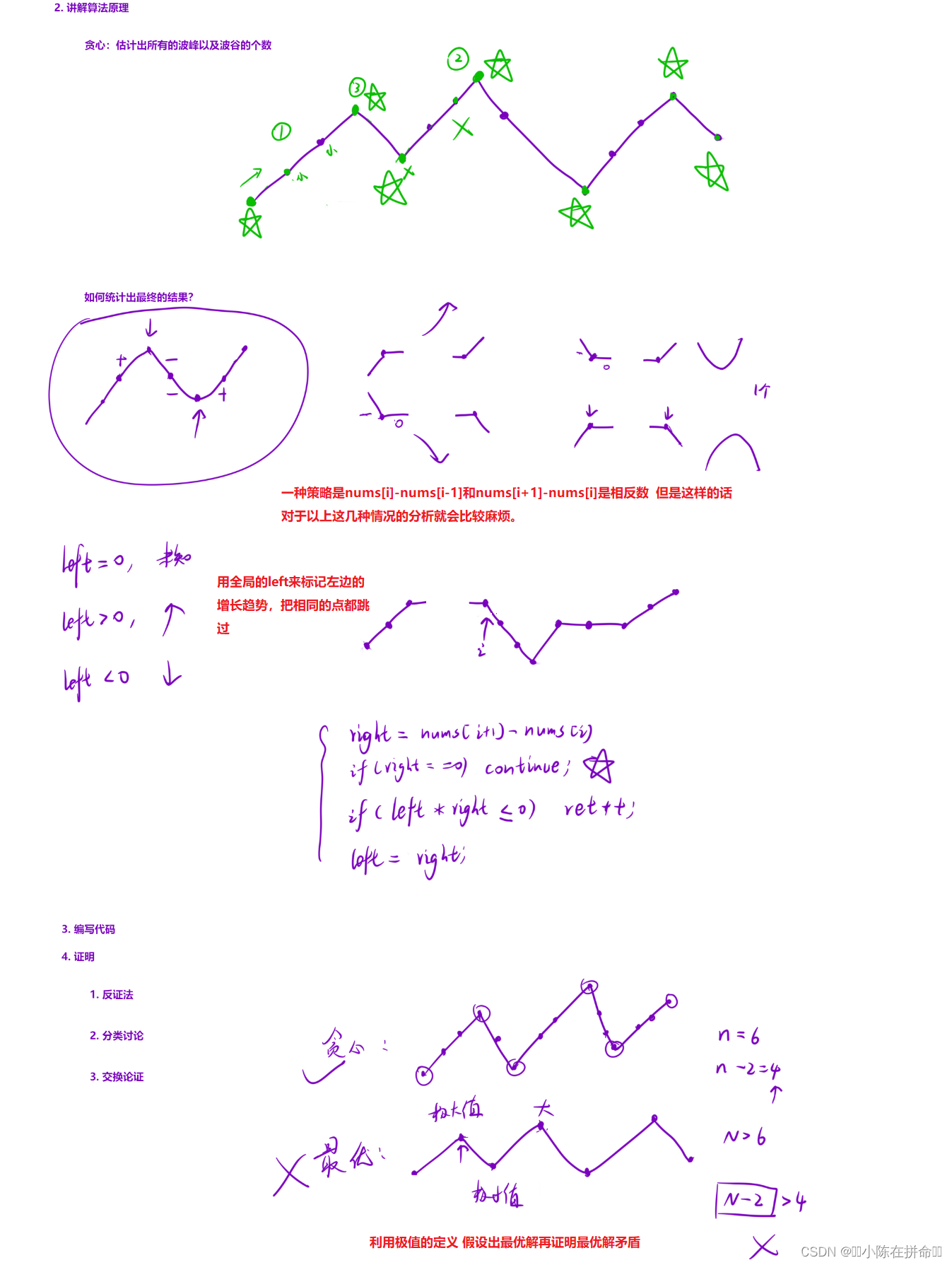
class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) 
    {
        int n=nums.size();
        if(n<2) return n;
      //总是选择当前的最优策略
       int left=0,ret=0; //left表示左边的状态
       for(int i=0;i<n-1;++i)
       {
        int right=nums[i+1]-nums[i];
        if(right==0) continue;//跳过相等的情况
        if(right*left<=0) ++ret;
        left=right;
       }
      return ret+1; //算上最后一个
    }
};

 六、最长递增子序列（交换论证）

. - 力扣（LeetCode）

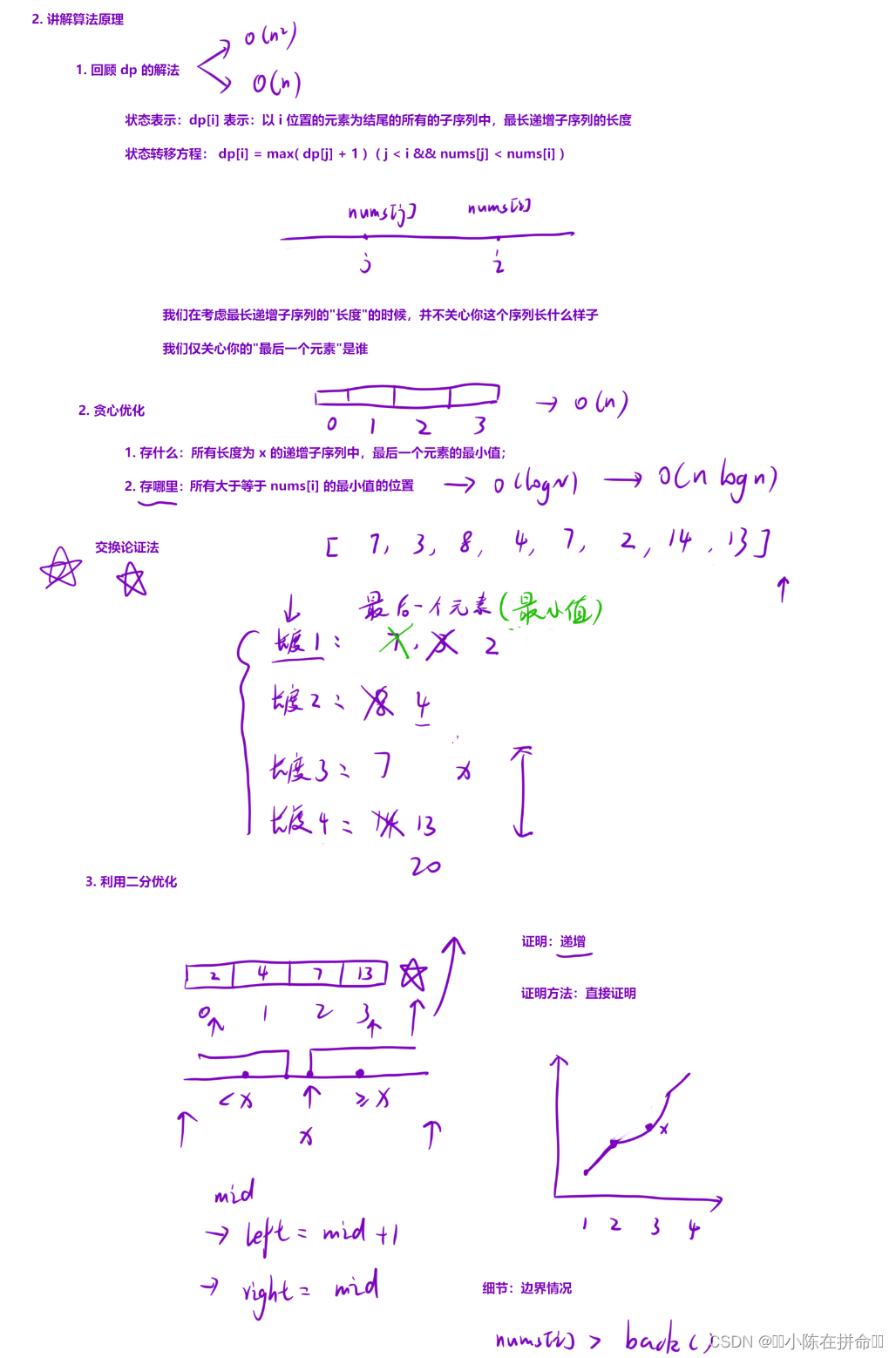
贪心+二分

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) 
    {
       //贪心+二分
       int n=nums.size();
       vector<int> ret;
       ret.emplace_back(nums[0]);
       for(int i=1;i<n;++i)
         //如果比最后一个数大 就直接尾插即可
         if(nums[i]>ret.back()) ret.emplace_back(nums[i]);
         //否则就用二分
         else 
         {
            int left=0,right=ret.size()-1;
            while(left<right)
            {
                int mid=(left+right)>>1;
                if(ret[mid]<nums[i]) left=mid+1;
                else right=mid;
            }
            ret[left]=nums[i];
         }
        return ret.size();
    }
};

 七、递增的三元子序列

. - 力扣（LeetCode）

贪心： 

class Solution {
public:
    bool increasingTriplet(vector<int>& nums) {
     //贪心策略
     int n=nums.size();
     if(n<3) return false;
     int first=nums[0];
     int second=INT_MAX;
     for(int i=1;i<n;++i)
        if(nums[i]>second) return true;
        else if(nums[i]>first) second=nums[i];
        else first=nums[i];//否则我肯定比较小 就得更新first
     return false;
    }
};

八、最长连续递增子序列

. - 力扣（LeetCode）

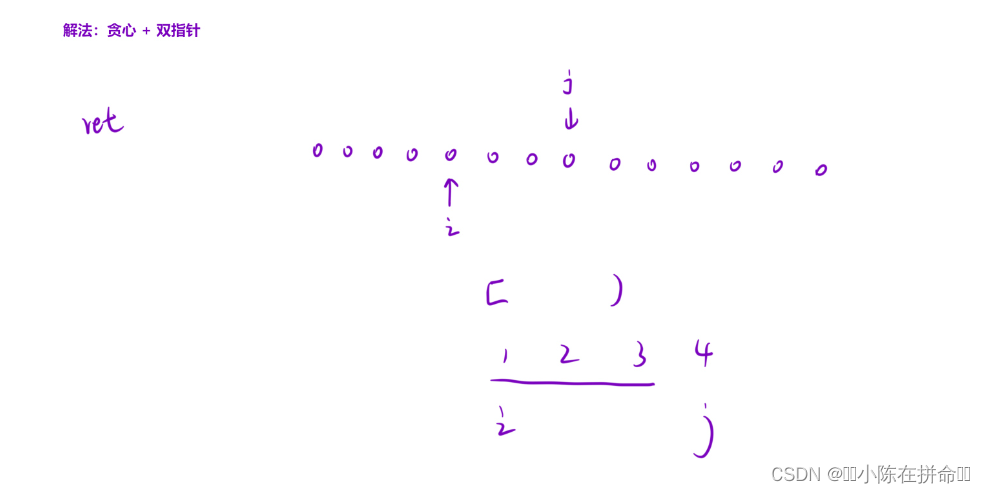
贪心+滑动窗口： 

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
     //贪心+双指针
     int ret=0;
     int n=nums.size();
     for(int i=0;i<n;)
     {
       int j=i+1;
       while(j<n&&nums[j]>nums[j-1]) ++j;
       ret=max(j-i,ret);
       i=j;
     }
     return ret;
    }
};