leetcode hot100_part30

上次写博客已经一个月了，这段时间在做外卖项目，真的啥也没有就是个小玩具。

上次接触是在最长递增子序列的一个题解里，复习一下已经忘完了。如果我们在一个有序数组中进行查找某个target，一般肯定就是从小到大or从大到小遍历查找，那么如果我们知道了有序数组的中间位置的数据的具体值，我们就可以只搜索数组的某一半来找target，这就是二分查找。

等号细节

首先 left 和 right 分别指向首尾，细节的点是

while( left ?? right ) 里的条件是小于还是小于等于
if ( nums [mid] < target) left = mid + 1 还是 mid

结合代码随想录的视频，首先弄清想写的是开区间还是闭区间，怎么写取决于你的定义，

如果是 [ left，right ] 也就是说搜索区间为左闭右闭，那么当 left == right 的时候是合法区间，可以相等，比如[1,1]，所以 <=。
继续，那么当 nums [mid] < target 的时候，我们可以肯定确定，mid不是我们要找的数，不在搜索区间内了，因为我们定义的是左闭右闭区间，所以搜索的区间更新为了[ mid +1, right ]，即 left = mid + 1，如果 left 还等于 mid，在 left 和 right 相邻的时候会死循环。

容易理解并写出左闭右开区间的代码，但左闭右开的时候 right 不是length - 1而是 length。其他区间的开闭写法以此类推。

//左闭右闭
while(left <= right){
    mid = left + ((right-left) >> 1);
    if(nums[mid] > target)
        right = mid - 1;
    else if(nums[mid] < target)
        left = mid + 1;
    else
        return mid;
}
return -1;



//左闭右开
right = nums.length;
while(left < right){
    mid = left + ((right-left) >> 1);
    if(nums[mid] > target)
        right = mid;
    else if(nums[mid] < target)
        left = mid + 1;
    else
        return mid;
}
return -1;

找上下界

参考：📝【LeetCode】一个模板通杀所有「二分查找」问题 (imageslr.com)

什么是上下界已经不重要了，这里简单说，就是如果有很多target，怎么找到第一个和最后一个target 值的index 以及 target 区间的前一个和后一个的下标。

1.第一个 >= target 的位置：index_1

这里包含两种情况，首先是很多 target 的第一个位置，还有就是没有target，第一个比target大的位置，怎么写代码还是取决于你怎么定义，但是做出这个定义是有点难度的。

左闭右闭

我们采用左右闭区间的写法，怎么定义呢，我们定义：

所有小于 target 的元素都在 left 的左侧，不包含 left，即从[ 0，left -1 ] 的元素值都是小于target的。对应的：if ( nums[ mid ] < target ) left = mid + 1；
否则，也就是所有大于等于 target 的元素都在 right 的右侧，不包含right，即从[ right + 1，length -1 ]的值都是大于等于target的。对应的：if（nums[ mid ] > = targrt）right = mid -1;
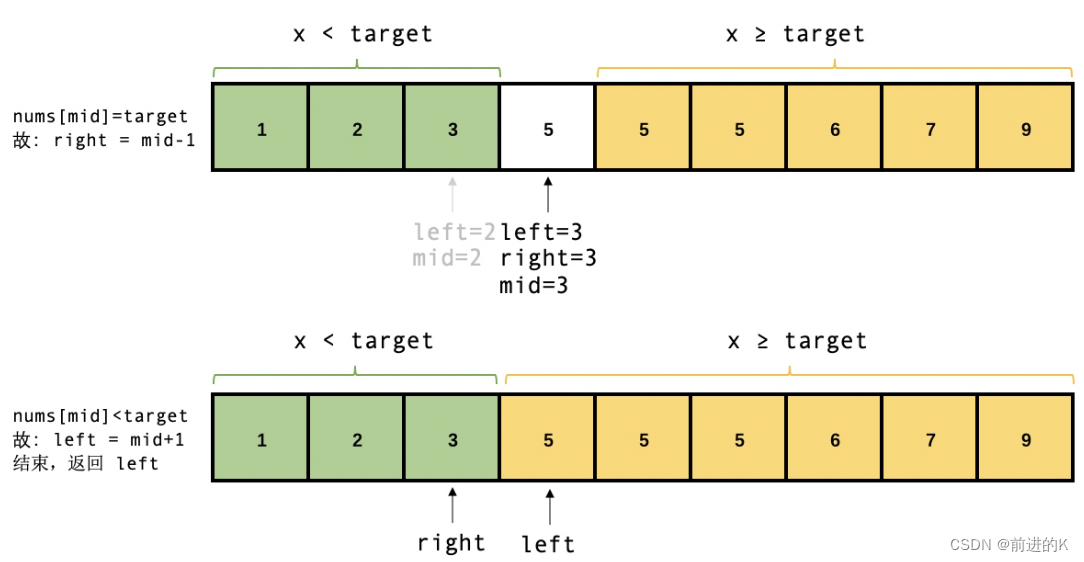
我们采用的是闭区间的写法，也就是说在while循环里最后区间肯定是不为空的，边界就是left和right指向同一个位置，跳出循环时肯定是 left在right的下一个位置，因为不论最后一步left还是right移动都是这个结果。如下图，target = 5；
那么就很显然了，最后的状态left在right的下一个位置，而right后面的根据我们的定义就是比targrt大的元素，而且数组是有序的，left就是我们要找的 index_1。

//left和right的初始化也要注意
while(left <= right){
    mid = left + ((right-left) >> 1);
    if(nums[mid] >= target)
        right = mid - 1;
    else left = mid + 1;
}
return left;

index_1其实也是顺序插入target的位置。如果要找的是第一个 > target 的元素，只要把上面代码里的 >= 改成 > 就行，其实最终的结果就是 left 侵入到了 right 右边的区间，相互侵入。

左闭右开

左闭右开的情况怎么写呢？首先right是length，然后while循环条件是小于，说明跳出循序的状态是 left == right，因为是[ left，right )，所以right更新的时候是 right = mid（此时right相当于上图黄色板块的第一个元素）。最后left和right指向一个位置，最后的搜索区间只有left，而不像左闭右闭那样为空。根据定义，[ 0，left -1 ]都是小于target 的元素，left是最后的区间结果，left == right 重合，即[ left，right )，[ right，length-1 ]是大于等于 target 的元素，所以 left 就是我们要的结果。

right = nums.length;     //变化1
while(left < right){     //变化2
    mid = left + ((right-left) >> 1);
    if(nums[mid] >= target)
        right = mid;     //变化3
    else left = mid + 1;
}
return left;              //变化4，返回right也可以

2.最后一个 <= target 的位置：index_2

如果有连续相等的target，那么结果就是最后一个 target 的位置，如果没有target，那么就是index_1的前一个位置。

按照上面的思考，是需要把上面的模版 > = 换成大于，然后返回 right 或者 left -1。关键的关键还是定义问题。left的左边全是 <= target 的元素。

3.target出现的第一个位置

其实就是index_1那种情况加个判断，先判断是否越界，再判断nums[ index_1 ] 是否为target

while(){
.....
}
if( left >= nums.length || nums[left] != target){
    return -1;
}
return left;

4.target出现的最后一个位置

index_2的变形，right是否越界，nums[ right ]是否为target

while(){
    //index_2代码
}
if(right < 0 || num[right] != target){
    return -1;
}
return right;

总结

关键在于分析出：

跳出while循环时左右指针的状态，相邻（left在right后面）还是重合
左右指针两侧值的含义，这个含义包不包括左右指针
左右相互入侵

题目

35.搜索插入位置

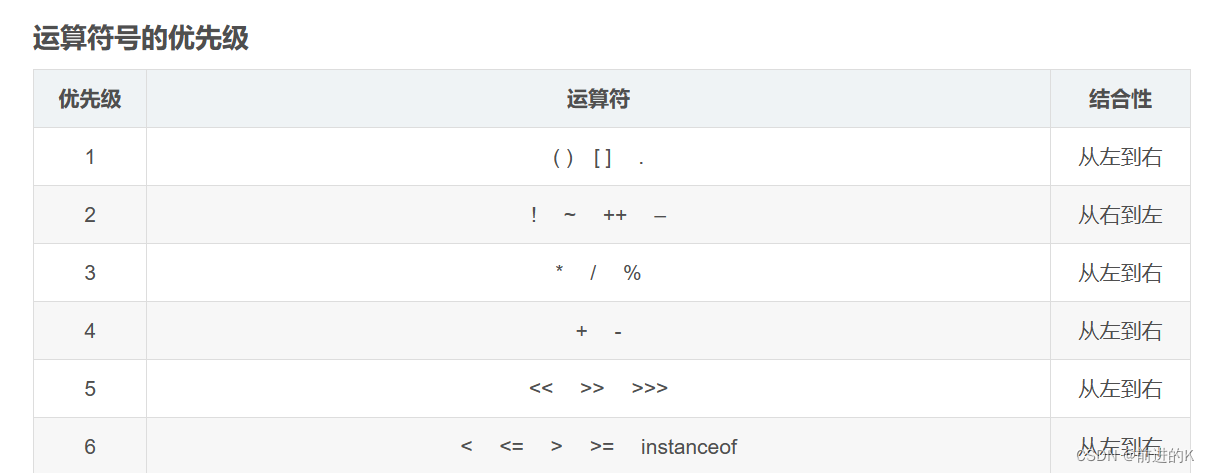
直接套index_1，这里发现了一个小问题，就是计算mid的时候，(right - left) >> 1这个外面要加括号，不能写成 mid = left + (right - left) >> 1，这样就超时了。因为+-运算符的优先级要比位运算高，上面模版一开始写错了，后面改的。

74.搜索二维矩阵

非严格递增就是存在相等的情况，严格递增就是没有等于的情况。

在矩阵中进行搜索，总体的思路是先找到 target 所在的行，然后再在那一行中寻找。

因为根据第二个条件，行到下一行的衔接处是严格严格递增的，能保证：我们在第一列中进行搜索，找到第一个大于 target 的行 x，它的上一行就是target所在的行。反证一下，如果target所在的行是 x - 2 行，那根据第二个条件，x - 1行的第一个数肯定比 target 大，那么找到的结果就是 x- 1行而不是x。

这里注意如果x是0，第0行，那target肯定是不存在的。

然后再目标行中进行寻找，找到第一个大于等于target的index,可行。但是为了代码复用，还是找的第一个大于target的index，同理如果index为0，target不存在。

最后对目标行的 index - 1 处进行判断是否等于target就行。