Python数据分析实战：利用ARIMA模型洞察股市规律

在这里插入图片描述

在股市中，数据的波动与变化风云莫测，难以捉摸。然而，借助科学的分析方法和工具，我们或许能够找到一些数据规律。今天，我们聊聊如何使用Python编程语言，结合ARIMA模型来洞察股市的变幻，为我们的投资决策提供有力支持。

ARIMA模型是经典的时间序列分析模型，它通过对历史数据的拟合和预测，揭示数据背后的动态依存关系。在股市数据分析中，ARIMA模型能够帮助我们理解股票价格、成交量等指标的变动趋势，预测未来的走势，从而做出更明智的投资决策。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-UMIC3b56-1721297882300)(https://i-blog.csdnimg.cn/direct/d84203b30e284286a0921280a7557c8c.jpeg#pic_center)]

一、分析思路

首先，调用财经接口包，获取股票数据，为了使用ARIMA模型研究开盘价的趋势，这里只关注date和open列，将date列转换为Pandas的datetime对象，并将它设置为索引。

然后，我们将对开盘价序列进行平稳性检验，接着进行差分运算，以确定ARIMA模型的阶数。

最后，我们将拟合ARIMA模型，并预测接下来一周的开盘价。

二、数据获取

TuShare是一个免费、开源的python财经数据接口包，主要实现对股票等金融数据从数据采集、清洗加工到数据存储的过程，能够为金融分析人员提供快速、整洁、和多样的便于分析的数据，为他们在数据获取方面极大地减轻工作量，使他们更加专注于策略和模型的研究与实现上。

考虑到Python pandas包在金融量化分析中体现出的优势，TuShare返回的绝大部分的数据格式都是DataFrame类型。本文数据来源于“中国卫星”股市交易数据，其中date 、 open 、high 、low 、close 、volumn、code各字段分别为股票日期、开盘价、最高价、最低价、收盘价、股票价格、股票编码。

#获取股票数据  
import tushare as ts  
#事先安装：!pip install -i https://pypi.tuna.tsinghua.edu.cn/simple tushare  
data = ts.get_k_data('600118', '2023-06-01','2024-05-31', ktype='D') #中国卫星600118  
# D--日线；W--周线；M--月线  
  
data.head()  
#导出数据  
data.to_csv('stock_ren.csv')

三、导入数据

导入端口下载的股票数据。

# 首先，我们需要读取上传的CSV文件以查看其内容。  
import pandas as pd  
# 读取上传的CSV文件  
file_path = 'stock_ren.csv'  
stock_data = pd.read_csv(file_path)  
  
# 显示文件的前几行，以了解数据的结构和内容  
stock_data.head()

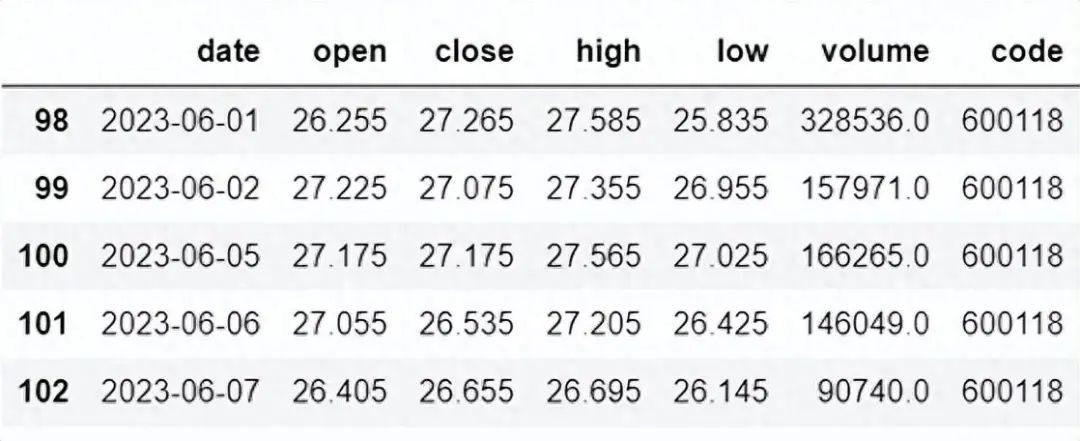
首先，我们将日期转换为datetime对象，并设置它为索引。



`# 将日期转换为datetime对象，并设置它为索引`

`stock_data['date'] = pd.to_datetime(stock_data['date'])`

`stock_data.set_index('date', inplace=True)`

`   `

`# 确认日期已正确设置为索引`

`stock_data.head()`

四、趋势分析

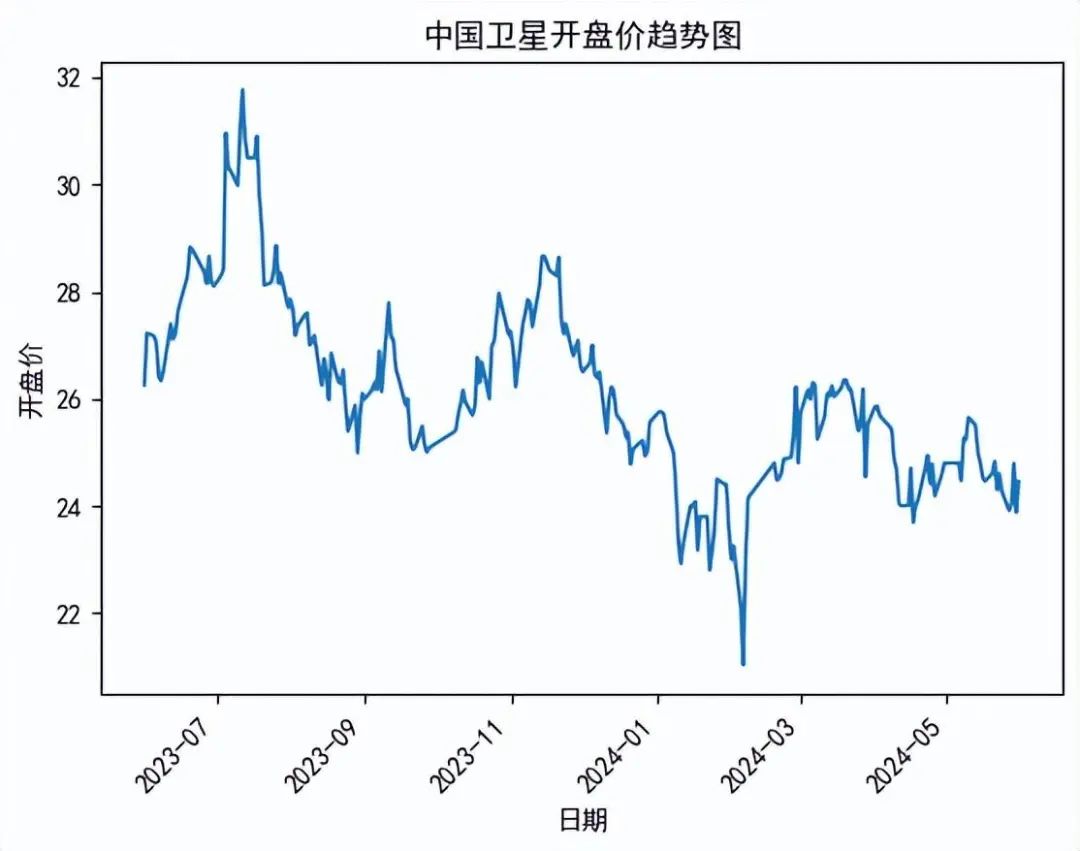
日期已成功转换为datetime对象，并设置为了索引。我们绘制时序图，通过时序图判断该股票开盘价的趋势。

plt.rcParams['font.sans-serif'] = ['simhei'] #用来正常显示中文标签  
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号  
stock_data['open'].plot()  
plt.title("中国卫星开盘价趋势图") #添加图标题  
plt.xticks(rotation=45) #横坐标旋转45度  
plt.xlabel('日期') #添加图的标签（x轴，y轴）  
plt.ylabel('开盘价')

五、平稳性检验

接下来对开盘价序列进行平稳性检验，平稳性检验通常是使用单位根检验，例如ADF检验。如果序列是非平稳的，我们将需要对其进行差分，直到它变得平稳，因为ARIMA模型要求输入序列必须是平稳的。

from statsmodels.tsa.stattools import adfuller
# 提取开盘价序列
open_price = stock_data['open']
# 执行ADF检验
result = adfuller(open_price)
adf_statistic = result[0]
p_value = result[1]
critical_values = result[4]



execution_result = f'ADF Statistic: {adf_statistic}, p-value: {p_value}, Critical Values: {critical_values}'
execution_result

"ADF Statistic: -2.0175512509905835,

p-value: 0.27893090334519033,

Critical Values: {‘1%’: -3.45, ‘5%’: -2.87, ‘10%’: -2.57}"

由于p-值大于0.05，我们不能拒绝序列存在单位根的原假设，这意味着开盘价序列是非平稳的。因此，我们需要对序列进行差分，直到它变得平稳。接下来对开盘价序列再进行一阶差分，并再次进行ADF检验来检查其平稳性。

六、差分运算

由于上面得出的结果是非平稳的，这里在进行一次差分，使其得到平稳的序列结果。

from statsmodels.tsa.stattools import adfuller
# 提取开盘价序列
open_price = stock_data['open']
# 执行ADF检验
result = adfuller(open_price)
adf_statistic = result[0]
p_value = result[1]
critical_values = result[4]



execution_result = f'ADF Statistic: {adf_statistic}, p-value: {p_value}, Critical Values: {critical_values}'
execution_result

`   `

`execution_result_diff = f'ADF Statistic (1st diff): {adf_statistic_diff}, p-value (1st diff): {p_value_diff}, Critical Values (1st diff): {critical_values_diff}'   execution_result_diff

"ADF Statistic (1st diff): -18.355654520506,

p-value (1st diff): 2.232193149282452e-30,

Critical Values(1st diff): {‘1%’: -3.45, ‘5%’: -2.87, ‘10%’: -2.57}"

一阶差分后的序列的p-值远小于0.05，因此我们可以拒绝存在单位根的原假设，这意味着差分后的序列是平稳的。我们现在可以继续使用差分后的序列来定阶ARIMA模型。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AKhXejG7-1721297882303)(https://i-blog.csdnimg.cn/direct/70f4511633c1452a8e298aaa68a6884b.png)]
七、模型定阶

ARIMA模型需要三个参数：p自回归项的阶数，d差分次数，和q移动平均项的阶数，这里已知d=1，因为我们进行了1次差分，为了确定p和q，可以使用**ACF（自相关函数）和PACF（偏自相关函数）**图。

下面绘制ACF和PACF图，以确定ARIMA模型的参数。

from statsmodels.graphics.tsaplots import plot_acf, plot_pacf  
import matplotlib.pyplot as plt  
  
# 设置图形的大小  
plt.figure()  
# 绘制ACF图  
plt.subplot(211)  
plot_acf(open_price_diff, lags=20, ax=plt.gca())  
# 绘制PACF图  
plt.subplot(212)  
plot_pacf(open_price_diff, lags=20, ax=plt.gca())  
  
# 显示图形  
plt.tight_layout()  
plt.show()

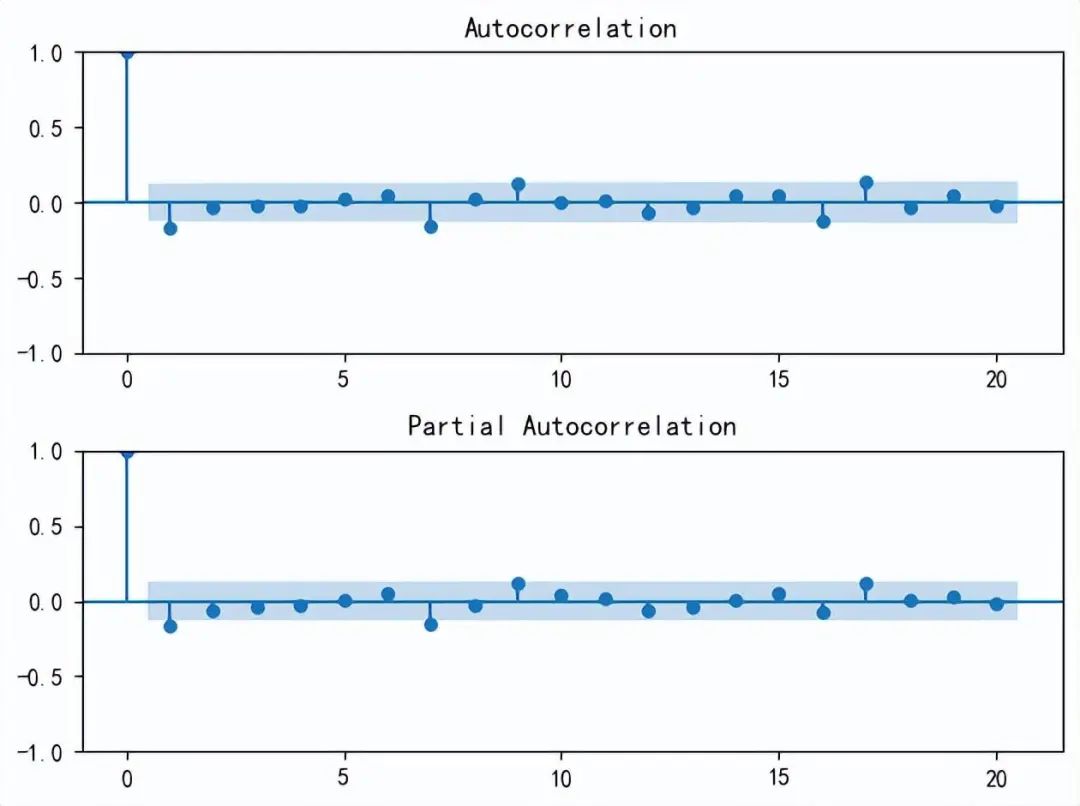
ACF（自相关函数）和PACF（偏自相关函数）图绘制完成，这些图帮助我们确定ARIMA模型的参数。在ACF图中，自相关函数在几阶滞后后会下降到置信区间内，这有助于判断MA项的阶数q，在PACF图中，偏自相关函数在几阶滞后后会下降到置信区间内，这有助于判断AR项的阶数p。

八、模型拟合

根据这些图，我们可以大致估计p和q的值，通常，我们会寻找图形中第一个显著的滞后，即第一个超出置信区间的峰值，由图可以拟合的模型是ARIMA(1,1,1)。

from statsmodels.tsa.arima.model import ARIMA  
import numpy as np  
  
# 拟合ARIMA(1,1,1)模型  
model = ARIMA(open_price, order=(1, 1, 1))  
model_fit = model.fit()  
  
# 显示拟合模型的摘要信息  
model_fit.summary()

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DfNStyLP-1721297882306)(https://i-blog.csdnimg.cn/direct/80119bd3da814439b7f5ae19586b88e1.png)]

ARIMA(1,1,1)模型的拟合结果已显示。模型的系数和统计检验结果如下：

AR项系数为-0.2496，标准误差为0.338，z值为-0.739，p值为0.460；
MA项系数为0.0999，标准误差为0.343，z值为0.292，p值为0.771；
方差为0.3738，标准误差为0.018。

模型的AIC值为634.438，BIC值为645.916。Ljung-Box Q检验的p值为1.00，Jarque-Bera检验的p值为0.00，表明模型残差是白噪声。但是，模型的系数的p值相对较高，表明这些系数可能不太显著。

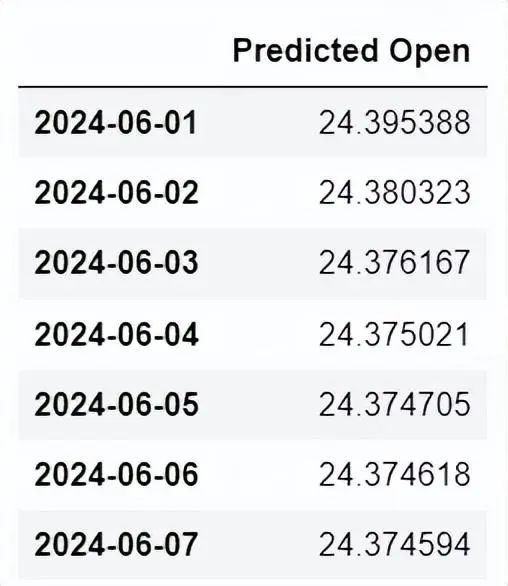
九、模型预测

为了预测接下来一周的开盘价，我们可以使用这个模型来进行数据预测，使用当前的ARIMA(1,1,1)模型来预测接下来一周的开盘价。根据ARIMA(1,1,1)模型，我们预测接下来一周的开盘价如下：

# 预测接下来一周的开盘价  
forecast_steps = 7  
forecast = model_fit.forecast(steps=forecast_steps)  
forecast_values = model_fit.forecast(steps=forecast_steps).values  
  
# 将预测结果转换为DataFrame  
forecast_index = pd.date_range(start=stock_data.index[-1], periods=forecast_steps + 1, closed='right')  
forecast_df = pd.DataFrame(data={'Predicted Open': forecast_values}, index=forecast_index)  
  
# 显示预测结果  
forecast_df

绘制原始开盘价数据和预测开盘价数据的折线图，用于对比预测值的差异。

# 绘制原始开盘价数据和预测开盘价数据的折线图
plt.figure()
# 绘制原始开盘价数据
plt.plot(stock_data.index, stock_data['open'], label='Original Open Price',)
# 绘制预测开盘价数据
plt.plot(forecast_df.index, forecast_df['Predicted Open'], label='Predicted Open Price', color='red', marker='x')


# 添加图例

plt.legend()
# 添加标题和轴标签
plt.title('Original vs Predicted Open Price')
plt.xlabel('Date')
plt.ylabel('Open Price')

# 显示图表
plt.show()

`   `

`# 添加图例`

`plt.legend()   # 添加标题和轴标签   plt.title('Original vs Predicted Open Price')   plt.xlabel('Date')   plt.ylabel('Open Price')      # 显示图表   plt.show()

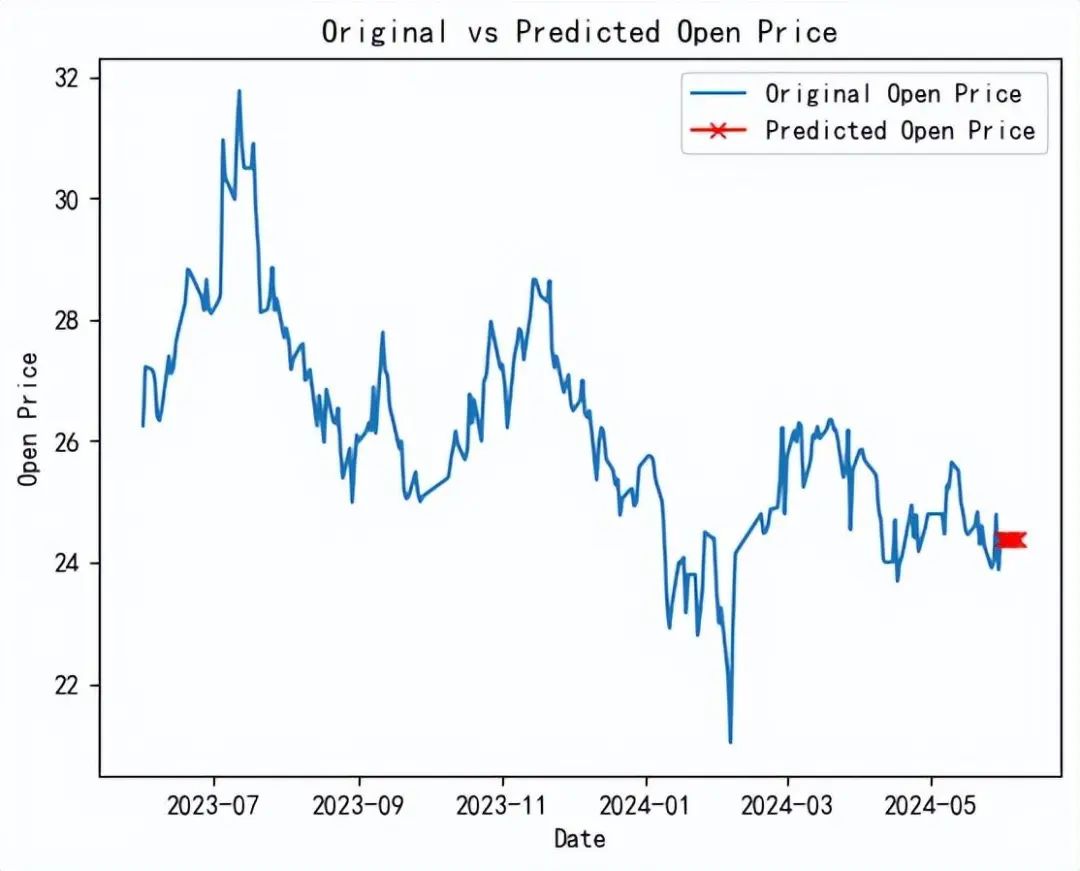
上图展示了原始开盘价数据和预测开盘价数据的对比，从图中可以看出，预测值与原始数据大致吻合。经过上面的实战演练，我们不难发现，ARIMA模型在股市数据分析中确实具有强大的应用潜力，掌握这种分析工具可以帮助我们更好的发现股市规律。

由于文章篇幅有限，文档资料内容较多，需要这些文档的朋友，可以加小助手微信免费获取，【保证100%免费】，中国人不骗中国人。

                                     **（扫码立即免费领取）**

全套Python学习资料分享：

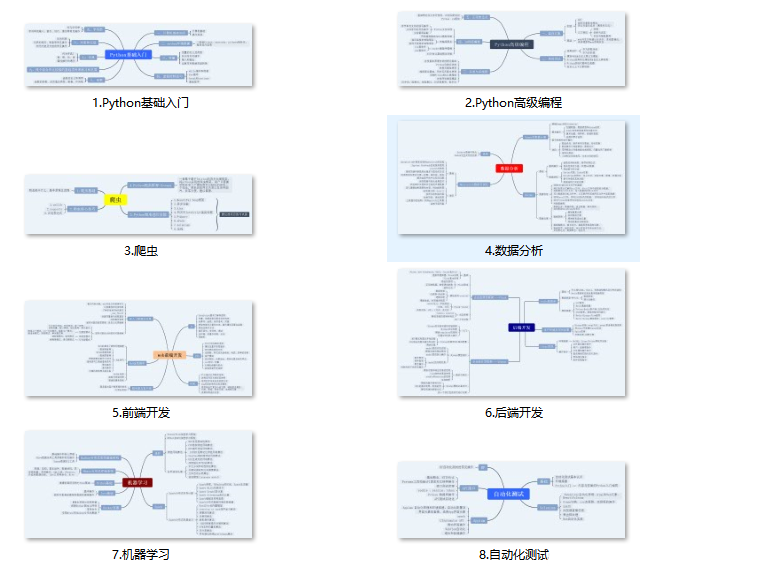
一、Python所有方向的学习路线

Python所有方向路线就是把Python常用的技术点做整理，形成各个领域的知识点汇总，它的用处就在于，你可以按照上面的知识点去找对应的学习资源，保证自己学得较为全面。

二、学习软件

工欲善其事必先利其器。学习Python常用的开发软件都在这里了，还有环境配置的教程，给大家节省了很多时间。

三、全套PDF电子书

书籍的好处就在于权威和体系健全，刚开始学习的时候你可以只看视频或者听某个人讲课，但等你学完之后，你觉得你掌握了，这时候建议还是得去看一下书籍，看权威技术书籍也是每个程序员必经之路。

四、入门学习视频全套

我们在看视频学习的时候，不能光动眼动脑不动手，比较科学的学习方法是在理解之后运用它们，这时候练手项目就很适合了。

五、实战案例

光学理论是没用的，要学会跟着一起敲，要动手实操，才能将自己的所学运用到实际当中去，这时候可以搞点实战案例来学习。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0jyjox8A-1721297882309)(https://i-blog.csdnimg.cn/direct/be8cae709a724a8498fef488a8496061.jpeg#pic_center)]