C++八数码程序图形化界面[2023-02-02]

news2024/11/24 8:50:55

C++八数码程序图形化界面[2023-02-02]

问题简介
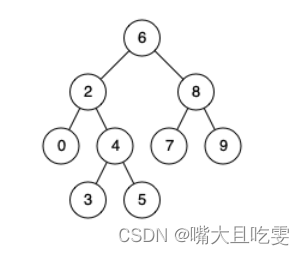
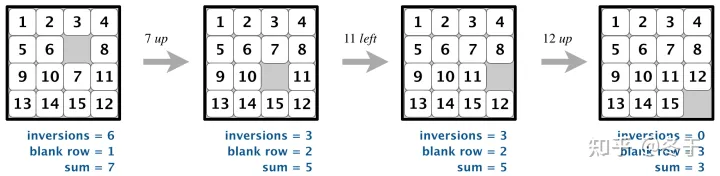
八数码：是指在3x3的矩阵中，其中有8个格子放置成1-8，剩下一个格子是空格。能够移动和空格相邻的格子到空格，直到这个矩阵满足每一行依次从左到右读取是有序，得到最后得到1-8有序，最后一个格子是空格。下图展示了一个案例：

1.png

推广二维N×N的棋盘
对于任意大小的二维N×N的棋盘：

2.png

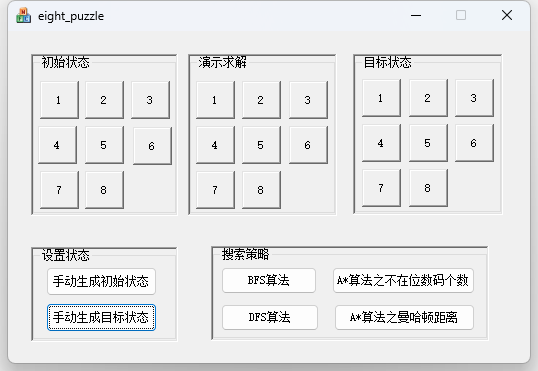
程序界面截屏

程序截屏.png

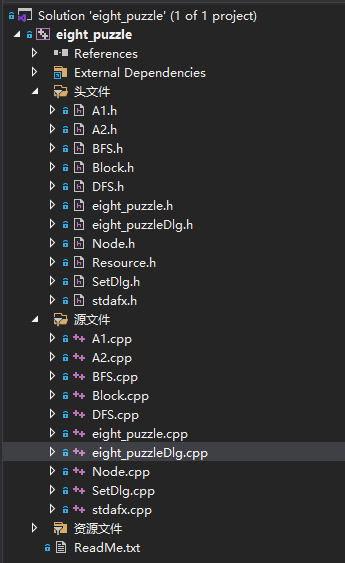
工程项目

工程项目.png

部分代码（MFC）


UINT Ceight_puzzleDlg::BFSThread(LPVOID lParam)
{
	Ceight_puzzleDlg* dlg;
	dlg = (Ceight_puzzleDlg*)lParam;

	int step;
	char** path;
	int initial[9];
	int target[9];
	bool complete;
	path = new char*;
	dlg->block_a->GetNum(initial);
	dlg->block_b->GetNum(target);
	dlg->engine = new BFS;
	dlg->engine->Initialise(initial, target);
	complete = dlg->engine->GetResult(&step, path);
	if(complete == true)
	{
		CString str;
		int buf[9];
		dlg->block_a->GetNum(buf);
		dlg->block_c->SetNum(buf);
		dlg->block_c->DemoResult(step, *path);
		str.Format(_T("BFS算法\n移动次数：%d"), step);
		dlg->MessageBox(str, NULL, MB_ICONINFORMATION);

		dlg->engine->ExportFile(_T("BFS"), step, *path);	
	}
	else
	{
		dlg->MessageBox(_T("移动次数10000步内无解！"), NULL, MB_ICONINFORMATION);
	}
	free(dlg->engine);
	return 0;
}

UINT Ceight_puzzleDlg::DFSThread(LPVOID lParam)
{
	Ceight_puzzleDlg* dlg;
	dlg = (Ceight_puzzleDlg*)lParam;

	int step;
	char** path;
	int initial[9];
	int target[9];
	bool complete;
	path = new char*;
	dlg->block_a->GetNum(initial);
	dlg->block_b->GetNum(target);
	dlg->engine = new DFS;
	dlg->engine->Initialise(initial, target);
	complete = dlg->engine->GetResult(&step, path);
	if (complete == true)
	{
		CString str;
		int buf[9];
		dlg->block_a->GetNum(buf);
		dlg->block_c->SetNum(buf);
		dlg->block_c->DemoResult(step, *path);
		str.Format(_T("DFS算法\n移动次数：%d"), step);
		dlg->MessageBox(str, NULL, MB_ICONINFORMATION);

		dlg->engine->ExportFile(_T("DFS"), step, *path);
	}
	else
	{
		dlg->MessageBox(_T("移动次数10000步内无解！"), NULL, MB_ICONINFORMATION);
	}
	free(dlg->engine);
	return 0;
}

UINT Ceight_puzzleDlg::A1Thread(LPVOID lParam)
{
	Ceight_puzzleDlg* dlg;
	dlg = (Ceight_puzzleDlg*)lParam;

	int step;
	char** path;
	int initial[9];
	int target[9];
	bool complete;
	path = new char*;
	dlg->block_a->GetNum(initial);
	dlg->block_b->GetNum(target);
	dlg->engine = new A1;
	dlg->engine->Initialise(initial, target);
	complete = dlg->engine->GetResult(&step, path);
	if (complete == true)
	{
		CString str;
		int buf[9];
		dlg->block_a->GetNum(buf);
		dlg->block_c->SetNum(buf);
		dlg->block_c->DemoResult(step, *path);
		str.Format(_T("A*算法之不在位数码个数\n移动次数：%d"), step);
		dlg->MessageBox(str, NULL, MB_ICONINFORMATION);

		dlg->engine->ExportFile(_T("A"), step, *path);
	}
	else
	{
		dlg->MessageBox(_T("OPEN表长度10000内无解！"), NULL, MB_ICONINFORMATION);
	}
	free(dlg->engine);
	return 0;
}

UINT Ceight_puzzleDlg::A2Thread(LPVOID lParam)
{
	Ceight_puzzleDlg* dlg;
	dlg = (Ceight_puzzleDlg*)lParam;

	int step;
	char** path;
	int initial[9];
	int target[9];
	bool complete;
	path = new char*;
	dlg->block_a->GetNum(initial);
	dlg->block_b->GetNum(target);
	dlg->engine = new A2;
	dlg->engine->Initialise(initial, target);
	complete = dlg->engine->GetResult(&step, path);
	if (complete == true)
	{
		CString str;
		int buf[9];
		dlg->block_a->GetNum(buf);
		dlg->block_c->SetNum(buf);
		dlg->block_c->DemoResult(step, *path);
		str.Format(_T("A*算法之曼哈顿距离\n移动次数：%d"), step);
		dlg->MessageBox(str, NULL, MB_ICONINFORMATION);

		dlg->engine->ExportFile(_T("ASTAR"), step, *path);
	}
	else
	{
		dlg->MessageBox(_T("OPEN表长度10000内无解！"), NULL, MB_ICONINFORMATION);
	}
	free(dlg->engine);
	return 0;
}

源码

https://pan.baidu.com/s/1pq1Nwwo0hlc_J84F93HM4A?pwd=1111

如何判断问题是否有解？
结论
先说结论：

一个状态表示成一维的形式，求出：除0之外所有数字的逆序数之和，也就是每个数字前面比它大的数字的个数的和，称为这个状态的逆序。

若两个状态的逆序奇偶性相同，则可相互到达，否则不可相互到达。

N是奇数时，当且仅当当前棋盘的逆序对是偶数的时候有解。
N是偶数时，当且仅当当前棋盘的逆序对数加上空格所在的行(行数从0开始算)是奇数的时候有解。
证明
根据棋局的逆序对定义，不论N为奇数或偶数，空格在同一行的左右移动不会修改逆序对数的奇偶性；
不论N为奇数或偶数，空格上下移动，相当于跨过N-1个格子，那么逆序的改变可能为±N-1，±N-3，±N-5 …… ±N-2k-1。
此时，若N为偶数，空格上下移动，逆序对数的奇偶性必然改变：比如N=4时，当上下移动的时候，相当于一个数字跨过了另外三个格子，它的逆序可能±3或±1。
若N为奇数，空格上下移动，逆序对数的奇偶性保持不变：比如N=3时，当上下移动的时候，相当于一个数字跨过了另外三个格子，它的逆序可能±2或0。

所以：
当N为奇数时，空格上下左右移动都不改变奇偶性，当前棋盘的逆序对与目标状态逆序对的奇偶性相同时有解，当八数码问题中，目标状态的逆序对数为0（偶数），所以“N是奇数时，当且仅当当前棋盘的逆序对是偶数的时候有解”。
N为偶数时，空格每上下移动一次，奇偶性改变。称空格位置所在的行到目标空格所在的行步数为空格的距离（不计左右距离），若两个状态的可相互到达，则有，两个状态的逆序奇偶性相同且空格距离为偶数，或者，逆序奇偶性不同且空格距离为奇数数。否则不能。也就是说，当此表达式成立时，两个状态可相互到达：（状态1的逆序数 + 空格距离)的奇偶性==状态2奇偶性。空格距离=N-空格所在行数。

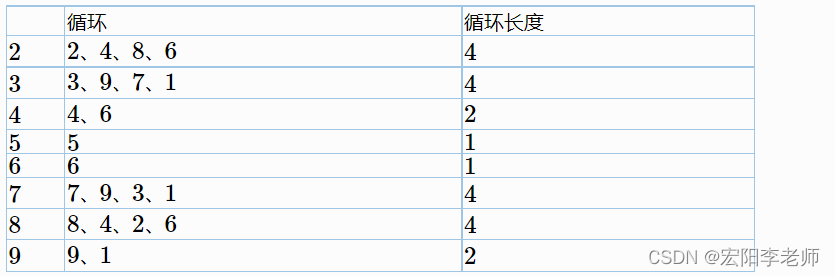
计算逆序对
可以利用归并排序时的“合并操作”来统计逆序对：

双指针i=0,j=0分别指向左半部分left和右半部分right的开始；
判断left[i]和right[j]的大小：
如果left[i]<=right[j]，没有逆序对，i+=1；
如果left[i]>right[j]，逆序对数为mid-i+1，j+=1；

解法
广度优先遍历穷举：让空格不断和周围位置交换，直到换到棋局变成目标棋局。

A star启发式穷举：优先在队列中从有可能更快达到目标棋局的棋局继续穷举。

广度优先遍历(bfs)
让空格不断和周围位置交换，交换后的棋局加入队列，注意使用哈希集合防止遍历重复的棋局，广度优先遍历结束的树高就是步数。

A star(A*)
A星算法是一种具备启发性策略的算法，优先在队列中从有可能更快达到目标棋局的棋局继续穷举。

更有可能达到目标棋局的当前棋局得分通过设置代价函数实现，为：已有的代价+未来的代价估计（可以使用曼哈顿、汉明距离等进行度量）。

所以只需要在计算当前棋局的代价，使用优先级队列，优先从代价较小的棋局继续穷举，就可能更快到达目标棋局。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/193361.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

爱普生LQ-610K针式打印机不通电维修

爱普生LQ-610K针式打印机不通电维修

基本参数： 爱普生LQ-610K是一台针式打印机，不支持网络打印，A4幅面，不支持自动双面打印。 品牌：爱普生Epson 型号：LQ-610K 颜色：灰色 类型：针式打印机 幅面：A4幅面 针数：24针 打印速度：中文（6.7cpi）150汉字/秒 100汉字/秒 （7.5cpi）168汉字/秒 112汉字/秒5…
阅读更多...
【整理分享】一些常见Vue面试题（附答案解析）

【整理分享】一些常见Vue面试题（附答案解析）

本次给大家分享一些关于Vue的常见面试题&#xff0c;带你梳理基础知识&#xff0c;增强Vue知识储备&#xff0c;值得收藏&#xff0c;快来看看吧&#xff01; Vue 常见面试题总结 MVVM模型&#xff1f; MVVM&#xff0c;是Model-View-ViewModel的简写&#xff0c;其本质是MVC…
阅读更多...
【Git笔记】GitHub创建远程库，推送到远程库，拉取到本地库与克隆到本地库

【Git笔记】GitHub创建远程库，推送到远程库，拉取到本地库与克隆到本地库

目录 创建 GitHub 远程库 创建远程库别名 推送本地库到远程库 拉取远程库到本地库 克隆远程库到本地库 创建 GitHub 远程库 点击 New repository Repository name 名字与工作区名称最好一致 Public 就是开源&#xff0c;Private 就是私有&#xff0c;不公开 其它的保持…
阅读更多...
阿里二面：千万级、亿级数据，如何性能优化？ 教科书级 答案来了

阿里二面：千万级、亿级数据，如何性能优化？ 教科书级 答案来了

说在前面 在尼恩指导了几百个小伙伴的面试&#xff0c;在这些过程中&#xff0c; 非常、非常高频的一个面试题&#xff1a; 千万级数据&#xff0c;如何做性能优化&#xff1f; 亿级数据&#xff0c;如何做性能优化&#xff1f; 最近&#xff0c;有个小伙伴阿里二面&#xff0…
阅读更多...
袁树雄有《早安隆回》，杨语莲有《汉川》，后者嫁给前者真是绝配

袁树雄有《早安隆回》，杨语莲有《汉川》，后者嫁给前者真是绝配

随着《早安隆回》的火爆&#xff0c;创作者袁树雄也收获颇丰&#xff0c;不但各种商演邀约不断&#xff0c;还坐到了春晚的观众席上。 、虽然对于袁树雄来说&#xff0c;他能够坐到观众席上面&#xff0c;就已经是一生的荣幸了&#xff0c;但是央视春晚纂改歌词&#xff0c;总是…
阅读更多...
python time模块和datetime模块详解

python time模块和datetime模块详解

一、time模块 time模块中时间表现的格式主要有三种&#xff1a; a、timestamp时间戳&#xff0c;时间戳表示的是从1970年1月1日00:00:00开始按秒计算的偏移量 b、struct_time时间元组&#xff0c;共有九个元素组。 c、format time 格式化时间&#xff0c;已格式化的结构使时间更…
阅读更多...
【生产者消费者模型】

【生产者消费者模型】

Linux生产者消费者模型生产者消费者模型生产者消费者模型的概念生产者消费者模型的特点生产者消费者模型优点基于BlockingQueue的生产者消费者模型基于阻塞队列的生产者消费者模型模拟实现基于阻塞队列的生产消费模型生产者消费者模型 生产者消费者模型的概念 生产者消费者模式…
阅读更多...
剑指 Offer 第19天 二叉树的公共祖先

剑指 Offer 第19天 二叉树的公共祖先

目录 剑指 Offer 68 - I. 二叉搜索树的最近公共祖先 剑指 Offer 68 - II. 二叉树的最近公共祖先 a 小部件 给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为&#xff1a;“对于有根树 T 的两个结点 p、q&#xff0c;最近公共祖先表…
阅读更多...
基于 JMeter 完成 Dubbo 接口的测试

基于 JMeter 完成 Dubbo 接口的测试

JMeter 默认是不支持 Dubbo 接口测试的&#xff0c;但是我们可以通过拓展的插件或 jar 包实现此功能。 JMeter 插件拓展 1.1 插件下载 测试 Dubbo&#xff0c;我们需要下载 Dubbo 的插件&#xff0c;在 Apache 的 Dubbo 插件 GitHub 中可以找到&#xff1a; https://github…
阅读更多...
DDR调试不通？先别扔，这个操作可能帮你逆袭！

DDR调试不通？先别扔，这个操作可能帮你逆袭！

作者&#xff1a;一博科技高速先生成员 黄刚相信大家过完一个美美的春节后&#xff0c;学习的热情一定会暴涨&#xff0c;反正高速先生给大家分享技术文章的热情是非常高涨的哈&#xff01;打从推出这个系列的仿真和理论相结合的话题后&#xff0c;文章受到了很多忠实粉丝的喜爱…
阅读更多...
ThinkPHP6 获取上传文件属性及自定义文件验证及上传处理

ThinkPHP6 获取上传文件属性及自定义文件验证及上传处理

TP^6.1文件上传有封装方法&#xff0c;如果不想用封装的&#xff0c;自定义上传怎么获取文件属性呢 目录 TP文件信息 打印上传文件信息 获取文件属性方法 1.获取文件大小&#xff08;单位bytes&#xff09; 2.获取文件后缀 3.获取文件上传路径 4.获取文件名称 5.上传文…
阅读更多...
XSS Challenges通关教程

XSS Challenges通关教程

11.XSS Challenges通关教程 Stage#1 直接在search 输入框中输入payload&#xff1a; <script>alert(document.domain)</script> 点击search就XSS攻击成功了。 Stage #2 尝试直接输入<script>alert(document.domain)</script>&#xff0c;发现并未…
阅读更多...
【2005NOIP普及组】T4.循环 代码解析

【2005NOIP普及组】T4.循环 代码解析

【2005NOIP普及组】T4.循环 代码解析 时间限制: 1000 ms 内存限制: 65536 KB 【题目描述】 乐乐是一个聪明而又勤奋好学的孩子。他总喜欢探求事物的规律。一天，他突然对数的正整数次幂产生了兴趣。 众所周知，2的正整数次幂最后一位数总是不断的在重复2，4，8，6，2，…
阅读更多...
使用PyTorch构建卷积神经网络（CNN）源码（详细步骤讲解+注释版） 01 手写数字识别

使用PyTorch构建卷积神经网络（CNN）源码（详细步骤讲解+注释版） 01 手写数字识别

1 卷积神经网络&#xff08;CNN&#xff09;简介 在使用PyTorch构建GAN生成对抗网络一文中&#xff0c;我们使用GAN构建了一个可以生成人脸图像的模型。但尽管是较为简单的模型&#xff0c;仍占用了1G左右的GPU内存&#xff0c;因此需要探索更加节约资源的方式。 卷积神经网络…
阅读更多...
vue 文件.env.production、.env.development简析

vue 文件.env.production、.env.development简析

静下来 慢慢看 首先 我们需要搭建一个项目 依赖包会自动下载好 无需自己 npm i .env 无论什么环境都会加载 .env.production 生产环境加载 .env.development 测试开发环境加载 我们下面的例子分开来写 只用 .env.production .env.development 在项目根目录新建两个文件 分别…
阅读更多...
Git和SVN

Git和SVN

一&#xff1a;两者的区别 ——Git是分布式版本控制系统&#xff0c;SVN是集中式版本控制系统 ——集中式版本控制系统 早期出现的版本控制系统有&#xff1a;SVN、CVS等&#xff0c;它们是集中式版本控制系统&#xff0c;集中式版本控制系统有一个单一的集中管理的服务器&…
阅读更多...
【微服务】分布式搜索引擎elasticsearch（2）

【微服务】分布式搜索引擎elasticsearch（2）

分布式搜索引擎elasticsearch&#xff08;2&#xff09;1.DSL查询文档1.1.DSL查询分类1.2.全文检索查询1.2.1.使用场景1.2.2.基本语法1.2.3.示例1.2.4.总结1.3.精准查询1.3.1.term查询1.3.2.range查询1.3.3.总结1.4.地理坐标查询1.4.1.矩形范围查询1.4.2.附近查询1.5.复合查询1…
阅读更多...
Power BI饼图

Power BI饼图

饼图展现的是个体占总体的比例&#xff0c;利用扇面的角度来展示比例大小。 在PowerBI默认的可视化对象中当然也有这种标准饼图&#xff0c;通过点击拖拽轻松生成&#xff0c; 通过对标题和图例的格式稍加设置&#xff0c;一个简单而不失专业的饼图就可以用了&#xff0c; 饼…
阅读更多...
学术加油站｜HIST，面向海量数据的学习型多维直方图

学术加油站｜HIST，面向海量数据的学习型多维直方图

编者按 本文系东北大学李俊虎所著&#xff0c;也是「 OceanBase 学术加油站」系列第九篇内容。 「李俊虎&#xff1a;东北大学计算机科学与工程学院在读硕士生&#xff0c;课题方向为数据库查询优化&#xff0c;致力于应用 AI 技术改进传统基数估计器&#xff0c;令数据库选择…
阅读更多...
mysql逻辑架构和数据库缓冲池

mysql逻辑架构和数据库缓冲池

逻辑架构 典型的CS架构&#xff0c;服务端程序使用的是mysqld 客户端进程向服务器进程发送一段文本&#xff08;SQL语句&#xff09;&#xff0c;服务器进程处理后再向客户端进程发送文本&#xff08;处理结果&#xff09; # 应用连接层: # 连接处理,用户鉴权(username,host…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023