RC-u1 热҈热҈热҈
分数 10
全屏浏览
切换布局
作者 DAI, Longao
单位 杭州百腾教育科技有限公司
热҈热҈热҈……最近热得打的字都出汗了!
幸好某连锁餐厅开启了气温大于等于 35 度即可获得一杯免费雪碧的活动。但不知为何,在每个星期四的时候,这个活动会暂停一天……
现在给定连续的若干天的气温情况以及给定的第一天是星期几,请你算出有多少天你可以喝到免费的雪碧,又有多少天是因为星期四而导致你喝不到雪碧的。
输入格式:
输入第一行是两个正整数 N, W (1≤N≤50,1≤W≤7),表示给定连续的 N 天,下面给定的第一天是星期 W(7 等于星期天)。
接下来的一行给出 N 个用一个空格隔开的、小于 60 的整数,第 i 个数表示第 i 天的温度。保证温度大于等于 -273 度。
输出格式:
输出两个数,第一个是你能喝到免费雪碧的天数,第二个是你本来能喝到免费雪碧、但因为是星期四而无法喝到的天数。
输入样例:
15 3 33 35 34 36 37 40 32 31 30 29 28 29 33 38 40输出样例:
5 1代码长度限制
16 KB
时间限制
400 ms
内存限制
64 MB
栈限制
8192 KB
思路:直接模拟
#include "bits/stdc++.h" using namespace std; int main(){ int n, w, x, ans1 =0, ans2 = 0; cin>>n>>w; for(int i = 0; i < n; i++){ cin>>x; if(x >= 35 && w != 4) ans1 ++; else if(x >= 35 && w == 4) ans2 ++; w ++; if(w == 8) w = 1; } cout<<ans1<<" "<<ans2; return 0; }
RC-u2 谁进线下了?
分数 15
全屏浏览
切换布局
作者 DAI, Longao
单位 杭州百腾教育科技有限公司
Xepa Legends 是一个第一人称射击类大逃杀(“吃鸡”)游戏,每轮游戏共有 20 支 3 人小队参加,最后获胜的队伍被称为“捍卫者”。
最近 Xepa Legends 举行了亚太地区南赛区的线上比赛,争夺 7 个前往德国曼海姆参加线下赛的资格,国内共有 14 支队伍参与到了其中。因为比赛十分激烈,直到最后谁进了线下仍有巨大的疑问。小 K 喜欢的国内知名战队 DreamTear 因其队内选手杀马特表现不佳,正好卡在出线分数前后,请你赶紧帮帮小 K,计算一下最后的分数情况,看看他喜欢的战队出线了没有吧!
Xepa Legends 的比赛共进行 N 场游戏,在每场游戏中,每支队伍在游戏中会获得一个排名和一个杀敌数(击败其他队伍玩家的数量),一支队伍在一场游戏的得分为杀敌数+排名分,排名分由队伍当场的排名根据以下表格求得:
排名 分数 第一名 12 分 第二名 9 分 第三名 7 分 第四名 5 分 第五名 4 分 第六名至第七名 3 分 第八名至第十名 2 分 第十一名至第十五名 1 分 第十六名至第二十名 0 分 例如,
- DreamTear 战队在第三场比赛获得了第三名、有 6 个杀敌数,那么他们将获得 7 + 6 = 13 分;
- KV 战队在第二场比赛获得了第 19 名、有 1 个杀敌数,那么他们将获得 0 + 1 = 1 分;
- SRN 战队在第四场比赛获得了第 1 名、有 9 个杀敌数,那么他们将获得 12 + 9 = 21 分。
注:本题与实际情况无关,所有比赛规则、队伍、队员名称均为虚构。
输入格式:
输入第一行是一个正整数 N (≤20),表示有 N 场比赛。
接下来有 N 部分输入,每部分是一场比赛的情况。对每一场比赛,信息共分 20 行,第 i 行(i=1,⋯,20)给出的两个非负整数 p 和 k 表示第 i 支队伍在这场比赛里获得了第 p 名、杀敌数为 k。
数据保证所有给定的情况中,排名永远大于等于 1 且小于等于 20,杀敌数小于等于 57。
输出格式:
输出 20 行,按编号从小到大依次输出队伍的编号及该队全部游戏结束时的总分。
输入样例:
3 6 2 7 3 11 5 10 1 2 9 5 8 14 3 4 3 1 6 18 1 12 1 20 0 13 0 3 2 16 4 8 1 19 0 9 4 17 1 15 0 8 2 19 1 12 2 1 9 10 1 7 5 18 0 14 0 5 2 4 4 2 5 6 2 16 3 13 1 20 0 3 7 9 3 15 0 17 5 11 3 18 0 5 2 2 9 9 4 4 7 10 3 16 0 1 6 20 0 15 1 6 0 3 6 14 3 7 4 19 0 17 0 8 9 11 0 13 5 12 0输出样例:
1 9 2 13 3 27 4 30 5 33 6 25 7 4 8 27 9 24 10 12 11 19 12 18 13 8 14 18 15 4 16 17 17 16 18 8 19 12 20 6代码长度限制
16 KB
时间限制
400 ms
内存限制
64 MB
栈限制
8192 KB
思路:模拟
#include "bits/stdc++.h" using namespace std; int rank1[30] = {0, 12, 9, 7, 5, 4, 3, 3, 2, 2, 2, 1 , 1, 1, 1, 1, 0 ,0,0,0,0}; int score[30]; int main(){ int T, x, y; cin>>T; while(T--){ for(int i = 1; i <= 20; i ++){ cin>>x>>y; score[i] += rank1[x]; score[i] += y; } } for(int i = 1; i <= 20; i ++){ cout<<i<<" "<<score[i]; if(i != 20) cout<<endl; } return 0; }
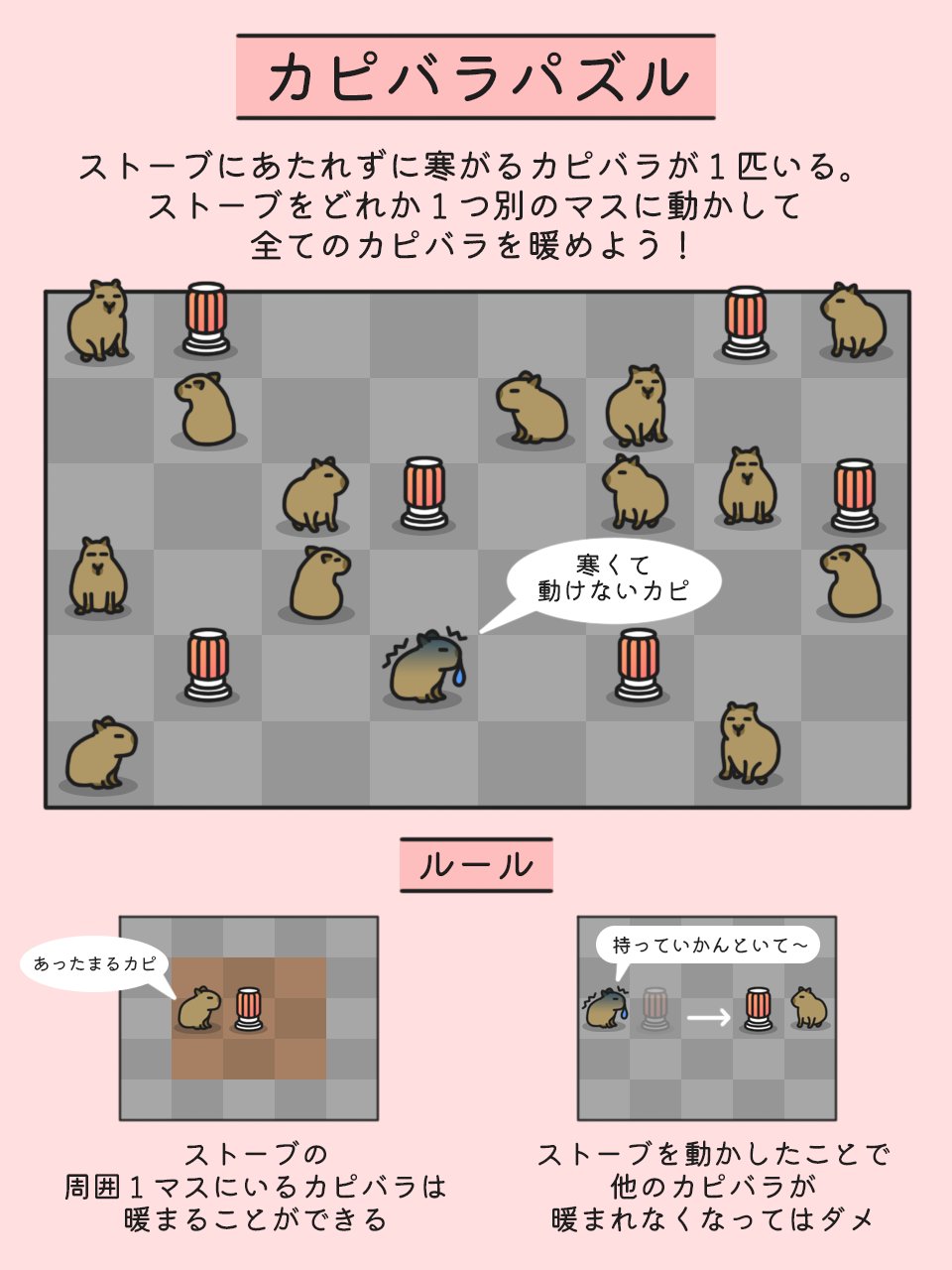
RC-u3 暖炉与水豚
分数 20
全屏浏览
切换布局
作者 DAI, Longao
单位 杭州百腾教育科技有限公司
PapiCon(@PapilloteContet)出了许多有意思的谜题,其中有一道关于水豚的谜题是这样的:
来源:x.com/PapilloteContet在一个 N×M 的矩阵中有若干水豚以及暖炉,暖炉可以辐射以它自身为中心的 3×3 范围里的水豚,使其变得暖呼呼的。谜题里存在一只冷的要命的水豚,你需要移动其中的一个暖炉,使所有水豚都变得暖呼呼的。
在往下读题前,如果你有兴趣的话,不妨思考一下如何解答这个谜题。(思考结果与题目无关,可跳过。)
这个谜题的关键在于,单纯从图中能看到的暖炉来说是无解的,但如果注意到,第 3 行第 6 列的水豚明明周围没有暖炉,却也处于暖呼呼的状态,就能推测出来图中的那个对话框挡住了一个暖炉,只要移动这个暖炉就可以完成题目的要求。
现在我们将谜题一般化,对于给定的一个 N×M 的矩阵、对应的所有水豚状态、以及能看到的暖炉摆放情况,已知最多只有一只水豚的状态不太对劲(周围没有暖炉却暖呼呼的),你需要推测有哪些格子可能藏了暖炉。一个空格可能藏了暖炉可以理解为:当前空格设置暖炉后整个矩阵的状态会从不合法变为合法。
输入格式:
输入第一行是两个正整数 N, M (1≤N,M≤1000),表示矩阵的大小。
接下来的 N 行,每行有 M 个字符,第 i 行的第 j 个字符表示矩阵中对应位置的状态,其中:
.表示空格(或者说,看上去是空格的格子);c表示很冷的水豚;w表示暖呼呼的水豚;m表示暖炉。输出格式:
输出若干行,每行两个正整数 r 和 c,表示第 r 行第 c 列有可能藏了一个暖炉,有多个可能时,先按 r 从小到大输出,r 相同时再按 c 从小到大输出。如果没有一个格子可能藏了暖炉, 则在一行中输出
Too cold!。
行与列均从 1 开始编号。输入样例:
6 8 wm....mw .w..ww.. ..wm.wwm w.w....w .m.c.m.. w.....w.输出样例:
2 7 3 5 4 6 4 7代码长度限制
16 KB
Java (javac)
时间限制
800 ms
内存限制
256 MB
其他编译器
时间限制
400 ms
内存限制
64 MB
栈限制
8192 KB
思路:暴力, 看热鼠鼠(水豚)一圈是否有炉子
#include "bits/stdc++.h" using namespace std; int n, m; typedef pair<int, int> PI; int dir[8][2] = {0, 1, 0, -1, 1, 0, -1, 0, -1, -1, 1, 1, -1, 1, 1, -1}; char a[1100][1100]; int vis[1100][1100]; vector<PI> vv; map<PI, int> mp; int ans = 0; void dfs(){ for(int k = 0; k < n; k ++){ for(int h = 0; h < m; h ++){ int x = k, y = h; if(a[x][y] == 'w'){ int flag = 0; for(int i = 0; i < 8; i ++){ int x1 = x + dir[i][0], y1 = y + dir[i][1]; if(x1 < 0 || x1 >= n || y1 < 0 || y1 >= m ) continue; if(a[x1][y1] == 'm'){ flag = 1; break; } } if(!flag) { for(int i = 0; i < 8; i ++){ int x1 = x + dir[i][0], y1 = y + dir[i][1]; if(x1 < 0 || x1 >= n || y1 < 0 || y1 >= m ) continue; if(a[x1][y1] == '.'){ mp[{x1, y1}] ++; } } } } if(a[x][y] == 'c'){ int flag = 0; for(int i = 0; i < 8; i ++){ int x1 = x + dir[i][0], y1 = y + dir[i][1]; if(x1 < 0 || x1 >= n || y1 < 0 || y1 >= m ) continue; if(a[x1][y1] == '.'){ mp[{x1, y1}]= -10000; } } } } } } int main(){ cin>>n>>m; for(int i = 0; i < n; i++){ for(int j = 0; j < m; j ++){ cin>>a[i][j]; } } dfs(); int xx = mp.size(); // cout<<xx<<endl; int ann = 0; for(auto x : mp){ if(x.second >= 1){ vv.push_back({x.first.first + 1, x.first.second + 1}); } } for(int i = 0; i < vv.size(); i ++){ cout<<vv[i].first<<" "<<vv[i].second; if(i != vv.size() - 1) cout<<endl; } if(vv.size() == 0) cout<<"Too cold!" ; return 0; }
RC-u4 章鱼图的判断
分数 25
全屏浏览
切换布局
作者 DAI, Longao
单位 杭州百腾教育科技有限公司
对于无向图 G=(V,E),我们将有且只有一个环的、大于 2 个顶点的无向连通图称之为章鱼图,因为其形状像是一个环(身体)带着若干个树(触手),故得名。
给定一个无向图,请你判断是不是只有一个章鱼子图存在。
输入格式:
输入第一行是一个正整数 T (1≤T≤5),表示数据的组数。
每组数据的第一行是两个正整数 N,M (1≤N,M≤105),表示给定的无向图有 N 个点,M 条边。
接下来的 M 行,每行给出一条边两个端点的顶点编号。注意:顶点编号从 1 开始,并且题目保证任何边不会重复给出,且没有自环。
输出格式:
对于每组数据,如果给定的图里只有一个章鱼子图,则在一行中输出
Yes和章鱼子图环的大小(及环中顶点数),其间以 1 个空格分隔。否则,则在一行中输出
No和图中章鱼子图的个数,其间以 1 个空格分隔。输入样例:
3 10 10 1 3 3 5 5 7 7 9 1 2 2 4 2 6 3 8 9 10 1 9 10 10 1 3 3 5 5 7 7 9 9 1 1 2 2 4 4 8 8 10 10 1 10 10 1 3 3 5 5 7 7 9 9 1 2 4 4 8 8 10 10 2 10 6输出样例:
Yes 5 No 0 No 2代码长度限制
16 KB
Java (javac)
时间限制
2500 ms
内存限制
512 MB
Python (python3)
时间限制
1400 ms
内存限制
512 MB
其他编译器
时间限制
1000 ms
内存限制
256 MB
栈限制
131072 KB
思路:就是先求有几个环(注意不是普通的环,而是题目给的章鱼环,也就是一个环里面的所有顶点只能参与组成一个环。然后如果只有一个环的话,再dfs求这个环的长度
ps:这个代码是凳子学长写的,我的只得了15分,超时了
#include <bits/stdc++.h> using namespace std; #define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); const int N=1e5+5; vector<int> edge[N]; bool flag[N],visited[N]; int res1,res2,node; // 用于求有几个环 void dfs(int s,int last) { visited[s]=true; flag[s]=true; // flag数组用于标记当前次dfs的结点 for(int i=0;i<edge[s].size();i++) { int nx=edge[s][i]; // last表示当前节点的上一个节点,因为是无向图 // 所以不能又遍历回去了,所以nx即下一个节点不能是last if(nx!=last) { if(flag[nx]) { // 如果下一个节点访问过了,说明成环了,则res2++ res2++; node=nx; // 并保留成环节点,用于求出环的节点个数 } else { dfs(nx,s); } } } } // 求环有几个节点 int dfs(int s,int last,int cnt) { flag[s]=true; for(int i=0;i<edge[s].size();i++) { int nx=edge[s][i]; if(nx!=last) { if(flag[nx]) { // 如果访问过了,说明成环了,返回节点个数 return cnt; } else { int res=dfs(nx,s,cnt+1); if(res!=0) return res; } } } flag[s]=false; return 0; } void solve() { for(int i=0;i<N;i++) edge[i].clear(),visited[i]=false; int n,m,from,to; cin>>n>>m; for(int i=1;i<=m;i++) { cin>>from>>to; edge[from].push_back(to); edge[to].push_back(from); } int cnt=0; for(int i=1;i<=n;i++) { res2=0,memset(flag,0,sizeof(flag)); if(visited[i]==false) { // visited的存在就是有样例三那种情况 dfs(i,0); res2/=2; // 由于在回溯的过程中,每个环都会被重复判断一次,画个图就好理解了,所以需要/=2 if(res2==1) { // 如果只有一个环,说明是一个章鱼图,则cnt++ cnt++; } } } if(cnt==1) { // 如果只有一个章鱼图 memset(flag,0,sizeof(flag)); res1=dfs(node,0,1); // 求环节点个数 cout<<"Yes"<<" "<<res1<<endl; } else cout<<"No"<<" "<<cnt<<endl; } int main() { IOS; int T=1; cin>>T; while(T--) { solve(); } return 0; }上面那个是学长写的
下面这个是我写的
#include "bits/stdc++.h" using namespace std; const int N = 1e5 + 10; vector<int> v[N]; int vis[N]; int res; vector<int> path; vector<vector<int> > finalResult; map<int, int> mp; bool isSame(vector<int> x, vector<int> y){ if(x.size() != y.size()) return false; else { sort(x.begin(),x.end()); sort(y.begin(),y.end()); return x == y; } } bool isExist(vector<int> x){ for(int i = 0; i < finalResult.size(); i ++){ if(isSame(finalResult[i], x)) return true; } return false; } void dfs(int x, int t){ if(x == t){ path.push_back(x); if(path.size() > 2 && !isExist(path)){ mp[x] ++; finalResult.push_back(path); } path.pop_back(); vis[x] = 0; return; } vis[x] = 1; path.push_back(x); for(int i = 0; i < v[x].size(); i ++){ int xx = v[x][i]; if(!vis[xx]) dfs(xx, t); } vis[x] = 0; path.pop_back(); } int main(){ ios::sync_with_stdio(false), cin.tie(0), cout.tie(0); int T; cin>>T; int a, b; int n, m; while(T--){ cin>>n>>m; mp.clear(); finalResult.clear(); for(int i = 1; i <= n; i ++){ v[i].clear(); } for(int i = 0; i < m; i ++){ cin>>a>>b; v[a].push_back(b); v[b].push_back(a); } for(int i = 1; i <= n; i ++){ for(int j = 0; j < v[i].size(); j ++){ dfs(v[i][j], i); } } if(finalResult.size() == 1) { res = finalResult[0].size(); cout<<"Yes"<<" "<<res; } else { int anss = 0; // for(int i = 0; i < finalResult.size(); i ++){ // mp[finalResult[i][finalResult[i].size() - 1]] ++; // } for(auto x : mp){ if(x.second == 1) anss ++; } cout<<"No"<<" "<<anss; } if(T != 0) cout<<endl; } return 0; }
RC-u5 工作安排
分数 30
全屏浏览
切换布局
作者 DAI, Longao
单位 杭州百腾教育科技有限公司
小 K 有 N 项工作等待完成,第 i 项工作需要花 ti 单位时间,必须在 di 时刻或之前完成,报酬为 pi。假设小 K 工作时刻从 0 开始,且同一时刻只能做一项工作、工作一旦开始则不可中断或切换至其他工作,请你帮小 K 规划一下如何选择合适的工作,使小 K 可以获得最多的报酬。
输入格式:
输入第一行是一个正整数 T (≤5),表示数据的组数。
接下来有 T 组数据,每组数据第一行是一个正整数 N (≤5000),表示待完成工作的数量。接下来的 N 行,每行三个非负整数 ti、di、pi (均 ≤5000;1≤i≤N),表示第 i 项工作需要花费的时间、截止时间以及报酬。
输出格式:
对于每组数据,输出小 K 能获得最多的报酬是多少。
输入样例:
3 5 1 2 50 3 3 100 1 5 1 3 2 5000 4 5 30 5 1 2 50 3 3 20 1 5 1 3 2 5000 4 5 30 5 1 2 50 3 3 100 1 5 1 3 2 5000 5 5 800输出样例:
101 80 800代码长度限制
16 KB
Java (javac)
时间限制
1000 ms
内存限制
256 MB
其他编译器
时间限制
400 ms
内存限制
64 MB
栈限制
8192 KB
思路:其实就是一个01背包,但是附加了时间的限制,这样的话我们按照时间进行排序,然后在进行dp就可以了 ,如果不加时间限制的话,如果是先遍历时间上靠后完成的任务,然后再遍历靠前的任务,那么靠前的任务的收益就加不上了,因为你后面那个不能再重来一遍了,其实就相当于你靠前的那个任务没做一样了。
#include "bits/stdc++.h" using namespace std; const int N = 5100; int t[N], d[N], p[N]; typedef long long ll; ll dp[N]; ll ans = 0, tt; int k = 0; struct node{ int t; int d; int p; bool operator < (const node & b)const { if(b.d != d) return d < b.d; else return p > b.p; } }; node a[N]; void f(int n){ for(int i = 0; i < n; i ++){ for(int j = a[i].d; j >= a[i].t; j --){ dp[j] = max(dp[j], dp[j - a[i].t] + a[i].p); if(dp[j] > ans){ ans = dp[j]; } } } } int main(){ int T; cin>>T; while(T--){ ll n , aa, b, c; ans = 0, tt = 0; cin>>n; memset(t, 0, sizeof(t)); memset(d, 0, sizeof(d)); memset(p, 0, sizeof(p)); memset(dp, 0, sizeof(dp)); k = 0; for(int i = 0; i < n; i++){ cin>>aa>>b>>c; if(aa <= b) a[k].t = aa, a[k].d = b, a[k ++ ].p = c, tt = max(tt, b); } sort(a, a + k); f(k); cout<<ans; if(T != 0) cout<<endl; } return 0; }