欢迎来到@一夜看尽长安花 博客,您的点赞和收藏是我持续发文的动力
对于文章中出现的任何错误请大家批评指出,一定及时修改。有任何想要讨论的问题可联系我:3329759426@qq.com 。发布文章的风格因专栏而异,均自成体系,不足之处请大家指正。

专栏:
- java全栈
- C&C++
- PythonAI
- PCB设计
文章概述:ACM算法 ——快排
关键词:ACM 快排
本文目录:
快速排序(quick sort)
原理
步骤
示例:
C语言版
C++版
算法特性
快速排序为什么快
基准数优化
示例:
尾递归优化
快速排序(quick sort)
是一种基于分治策略的排序算法,运行高效,应用广泛。
原理
快速排序的核心操作是“哨兵划分”,其目标是:选择数组中的某个元素作为“基准数”,将所有小于基准数的元素移到其左侧,而大于基准数的元素移到其右侧。具体来说,哨兵划分的流程如图 所示。
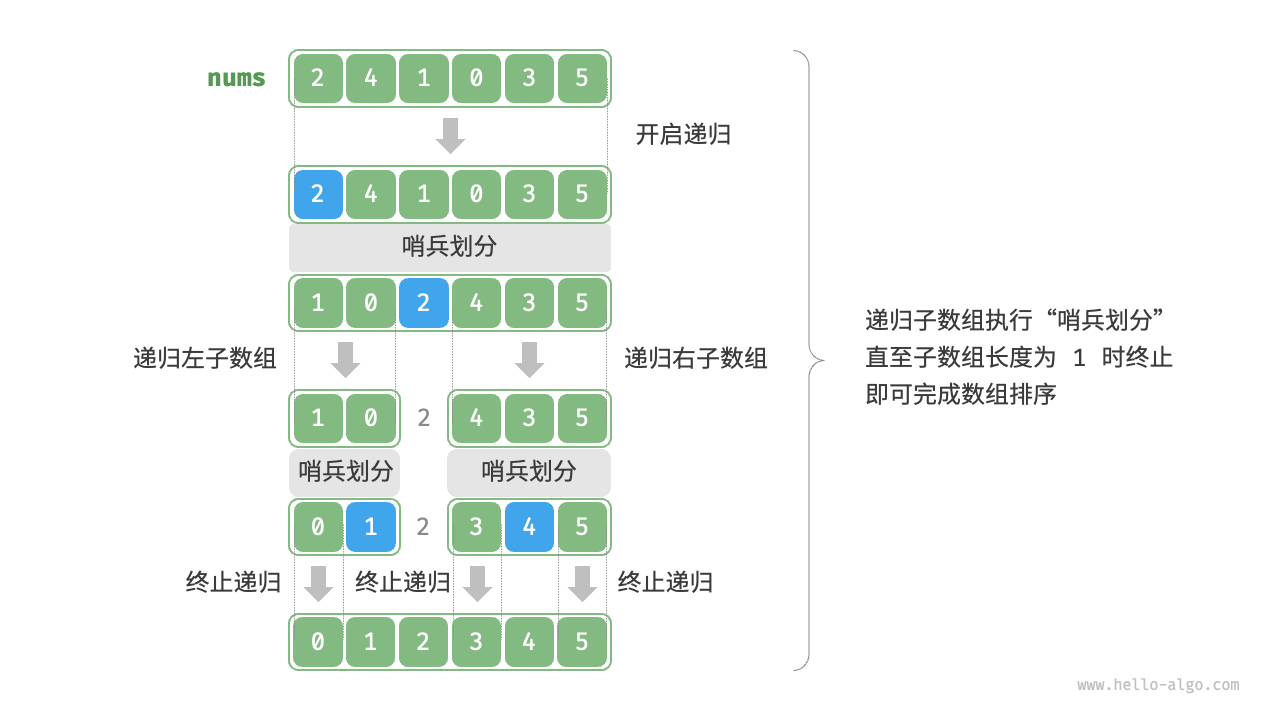
步骤
- 确定分界点X:
- 调整区间:
- 选取数组最左端元素作为基准数,初始化两个指针
i和j分别指向数组的两端。 - 设置一个循环,在每轮中使用
i(j)分别寻找第一个比基准数大(小)的元素,然后交换这两个元 素。 - 循环执行步骤
2.,直到i和j相遇时停止,最后将基准数交换至两个子数组的分界线。
- 递归处理左右两端
示例:
C语言版
#include <stdio.h>
#include <stdlib.h>
void swap(int *a, int *b)
{
int temp = *a;
*a = *b;
*b = temp;
}
void quick_sort(int q[], int l, int r)
{
if (l >= r) return;
int i = l - 1, j = r + 1, x = q[l+r >> 1];
while (i < j)
{
do i ++ ; while (q[i] < x);
do j -- ; while (q[j] > x);
if (i < j) swap(&q[i], &q[j]);
}
quick_sort(q, l, j), quick_sort(q, j + 1, r);
}
int main(void)
{
int n;
scanf("%d", &n);
int *q = (int *)malloc(n * sizeof(int));
if (q == NULL)
{
fprintf(stderr, "Memory allocation failed.\n");
return 1;
}
for (int i = 0; i < n; i++)
{
scanf("%d", &q[i]);
}
quick_sort(q, 0, n - 1);
for (int i = 0; i < n; i++)
{
printf("%d ", q[i]);
}
printf("\n");
free(q);
return 0;
}
C++版
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int n;
const int N = 100002;
int nums[N];
void quick_sort(int q[], int l, int r) {
if (l >= r) {
return;
}
int x = q[ l+r >> 1];
int i = l - 1, j = r + 1;
while (i < j) {
do i++; while (q[i] < x);
do j--; while (q[j] > x);
if (i < j) swap(q[i], q[j]);
}
quick_sort(q, l, j);
quick_sort(q, j + 1, r);
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", &nums[i]);
}
quick_sort(nums, 0, n - 1);
for (int i = 0; i < n; i++) {
printf("%d ", nums[i]);
}
return 0;
}
算法特性
- 时间复杂度为 𝑂(𝑛log𝑛)、自适应排序:在平均情况下,哨兵划分的递归层数为 log𝑛 ,每层中的总循环数为 𝑛 ,总体使用 𝑂(𝑛log𝑛) 时间。在最差情况下,每轮哨兵划分操作都将长度为 𝑛 的数组划分为长度为 0 和 𝑛−1 的两个子数组,此时递归层数达到 𝑛 ,每层中的循环数为 𝑛 ,总体使用 𝑂(𝑛2) 时间。
- 空间复杂度为 𝑂(𝑛)、原地排序:在输入数组完全倒序的情况下,达到最差递归深度 𝑛 ,使用 𝑂(𝑛) 栈帧空间。排序操作是在原数组上进行的,未借助额外数组。
- 非稳定排序:在哨兵划分的最后一步,基准数可能会被交换至相等元素的右侧。
快速排序为什么快
从名称上就能看出,快速排序在效率方面应该具有一定的优势。尽管快速排序的平均时间复杂度与“归并排序”和“堆排序”相同,但通常快速排序的效率更高,主要有以下原因。
- 出现最差情况的概率很低:虽然快速排序的最差时间复杂度为 𝑂(𝑛2) ,没有归并排序稳定,但在绝大多数情况下,快速排序能在 𝑂(𝑛log𝑛) 的时间复杂度下运行。
- 缓存使用效率高:在执行哨兵划分操作时,系统可将整个子数组加载到缓存,因此访问元素的效率较高。而像“堆排序”这类算法需要跳跃式访问元素,从而缺乏这一特性。
- 复杂度的常数系数小:在上述三种算法中,快速排序的比较、赋值、交换等操作的总数量最少。这与“插入排序”比“冒泡排序”更快的原因类似。
基准数优化
快速排序在某些输入下的时间效率可能降低。举一个极端例子,假设输入数组是完全倒序的,由于我们选择最左端元素作为基准数,那么在哨兵划分完成后,基准数被交换至数组最右端,导致左子数组长度为 𝑛−1、右子数组长度为 0 。如此递归下去,每轮哨兵划分后都有一个子数组的长度为 0 ,分治策略失效,快速排序退化为“冒泡排序”的近似形式。
为了尽量避免这种情况发生,我们可以优化哨兵划分中的基准数的选取策略。例如,我们可以随机选取一个元素作为基准数。然而,如果运气不佳,每次都选到不理想的基准数,效率仍然不尽如人意。
需要注意的是,编程语言通常生成的是“伪随机数”。如果我们针对伪随机数序列构建一个特定的测试样例,那么快速排序的效率仍然可能劣化。
为了进一步改进,我们可以在数组中选取三个候选元素(通常为数组的首、尾、中点元素),并将这三个候选元素的中位数作为基准数。这样一来,基准数“既不太小也不太大”的概率将大幅提升。当然,我们还可以选取更多候选元素,以进一步提高算法的稳健性。采用这种方法后,时间复杂度劣化至 𝑂(𝑛2) 的概率大大降低。
示例:
/* 选取三个候选元素的中位数 */
int medianThree(int nums[], int left, int mid, int right) {
int l = nums[left], m = nums[mid], r = nums[right];
if ((l <= m && m <= r) || (r <= m && m <= l))
return mid; // m 在 l 和 r 之间
if ((m <= l && l <= r) || (r <= l && l <= m))
return left; // l 在 m 和 r 之间
return right;
}
/* 哨兵划分(三数取中值) */
int partitionMedian(int nums[], int left, int right) {
// 选取三个候选元素的中位数
int med = medianThree(nums, left, (left + right) / 2, right);
// 将中位数交换至数组最左端
swap(nums, left, med);
// 以 nums[left] 为基准数
int i = left, j = right;
while (i < j) {
while (i < j && nums[j] >= nums[left])
j--; // 从右向左找首个小于基准数的元素
while (i < j && nums[i] <= nums[left])
i++; // 从左向右找首个大于基准数的元素
swap(nums, i, j); // 交换这两个元素
}
swap(nums, i, left); // 将基准数交换至两子数组的分界线
return i; // 返回基准数的索引
}尾递归优化
在某些输入下,快速排序可能占用空间较多。以完全有序的输入数组为例,设递归中的子数组长度为 𝑚 ,每轮哨兵划分操作都将产生长度为 0 的左子数组和长度为 𝑚−1 的右子数组,这意味着每一层递归调用减少的问题规模非常小(只减少一个元素),递归树的高度会达到 𝑛−1 ,此时需要占用 𝑂(𝑛) 大小的栈帧空间。
为了防止栈帧空间的累积,我们可以在每轮哨兵排序完成后,比较两个子数组的长度,仅对较短的子数组进行递归。由于较短子数组的长度不会超过 𝑛/2 ,因此这种方法能确保递归深度不超过 log𝑛 ,从而将最差空间复杂度优化至 𝑂(log𝑛)
C++版
#include <iostream>
#include <algorithm>
#include <cstdlib> // for rand() and srand()
#include <ctime> // for time()
using namespace std;
const int N = 100002;
int nums[N];
// 随机选择基准数并进行交换
int randomPartition(int nums[], int left, int right) {
int randomIndex = left + rand() % (right - left + 1);
swap(nums[left], nums[randomIndex]); // 将随机选择的基准数交换至数组最左端
int pivot = nums[left]; // 以 nums[left] 为基准数
int i = left + 1, j = right;
while (true) {
while (i <= right && nums[i] < pivot) i++;
while (j >= left && nums[j] > pivot) j--;
if (i >= j) break;
swap(nums[i], nums[j]);
i++;
j--;
}
swap(nums[left], nums[j]); // 将基准数交换至两子数组的分界线
return j; // 返回基准数的索引
}
// 快速排序,使用尾递归优化
void quick_sort(int nums[], int left, int right) {
while (left < right) {
int mid = randomPartition(nums, left, right);
if (mid - left < right - mid) {
quick_sort(nums, left, mid - 1);
left = mid + 1;
} else {
quick_sort(nums, mid + 1, right);
right = mid - 1;
}
}
}
int main() {
srand(time(0)); // 设置随机数种子
int n;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> nums[i];
}
quick_sort(nums, 0, n - 1);
for (int i = 0; i < n; i++) {
cout << nums[i] << " ";
}
return 0;
}
C语言版:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define N 100002
void swap(int* a, int* b) {
int temp = *a;
*a = *b;
*b = temp;
}
int randomPartition(int nums[], int left, int right) {
int randomIndex = left + rand() % (right - left + 1);
swap(&nums[left], &nums[randomIndex]);
int pivot = nums[left];
int i = left + 1, j = right;
while (1) {
while (i <= right && nums[i] < pivot) i++;
while (j >= left && nums[j] > pivot) j--;
if (i >= j) break;
swap(&nums[i], &nums[j]);
i++;
j--;
}
swap(&nums[left], &nums[j]);
return j;
}
void quick_sort(int nums[], int left, int right) {
if (left >= right) return;
int mid = randomPartition(nums, left, right);
quick_sort(nums, left, mid - 1);
quick_sort(nums, mid + 1, right);
}
int main() {
srand(time(0));
int nums[N];
int n, i;
scanf("%d", &n);
for (i = 0; i < n; i++) {
scanf("%d", &nums[i]);
}
quick_sort(nums, 0, n - 1);
for (i = 0; i < n; i++) {
printf("%d ", nums[i]);
}
printf("\n");
return 0;
}