一、 问题：

二、分析：

在讲解这道题之前，大家需要对线性区间DP和环形区间DP有一定的了解，因此如果不会这两个知识点的话，作者建议先去看一下作者之前写过的两篇文章：石子合并（分治+贪心+DP+前缀和）和AcWing 1068. 环形石子合并（环形区间DP）

在对这两个知识点都有了详细地了解之后，我们发现这道题唯一的区别就在于合并两堆石子的时候，吸收能量的方式并不是简单地相加。
除此以外和环形的区间DP是没有区别的。

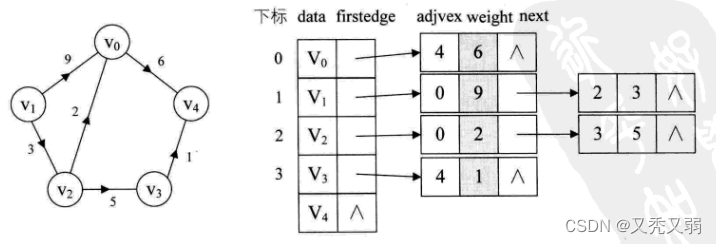
而这道题的合并方式可以画成下面这个图的样子：

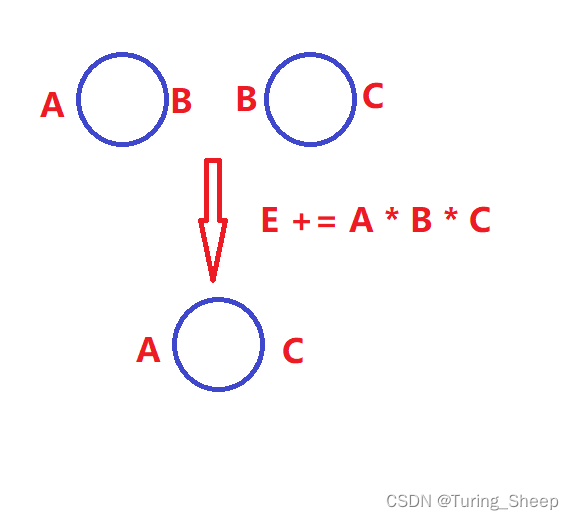
那么对于一个环上的能量而言，最终合并的效果又是什么样的呢？

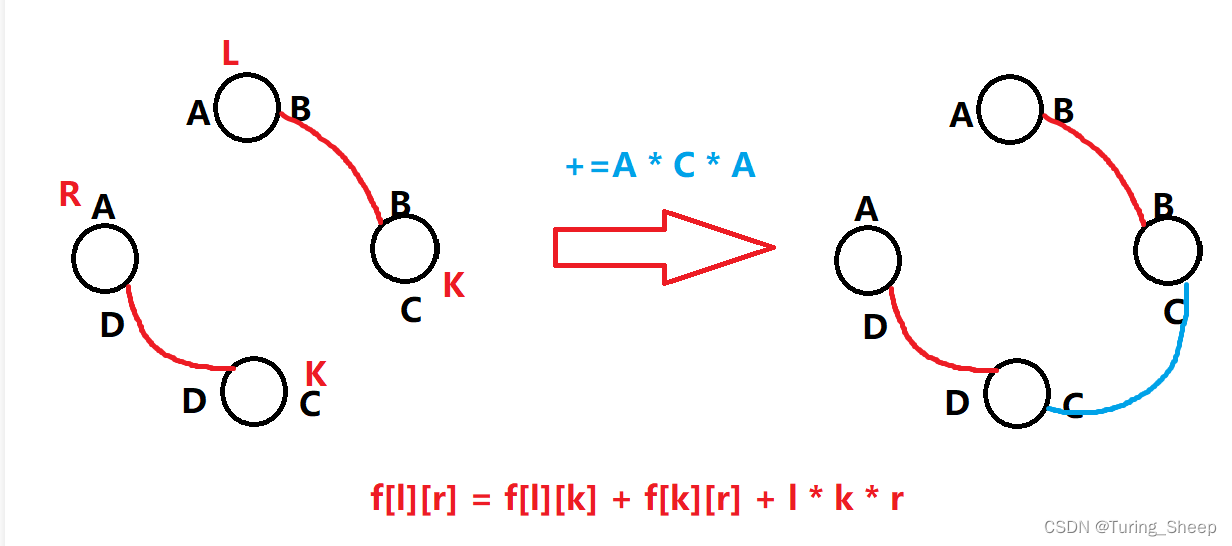
根据合并的方式我们可以映射到我们的转移方程之中，通过和之前两篇文章中的转移方程进行对比，我们发现，这个转移方程有两处不同，一处是由于能量吸收方式造成的最后一项所加的数不再是前缀和，另外一个是我们之前的k和k+1，但是这里是两个k。

那么除了转移方程的不同，还有什么不同呢？

我们接着看：

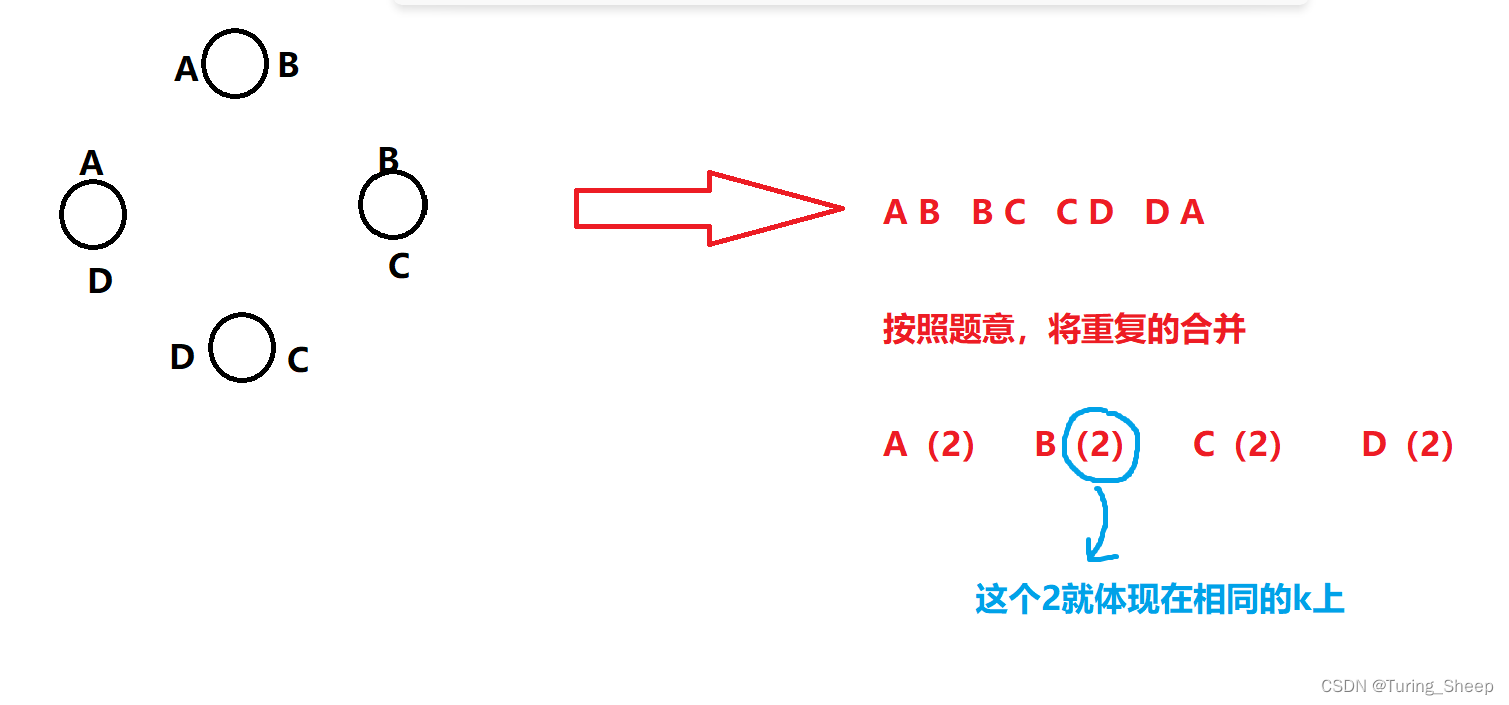
那么转化成最终的序列A，B，C，D对吗？

如果这么表示的话，假设我们还是提前将A和B合并，C和D合并，那么最终合并这两大堆的时候，就成了A * C * D了。因此，我们需要将两个A拆出一个放在末尾。

这么表示的话，我们才能够代表环。

所以此时我们就需要去计算长度为n + 1的序列。

那么环变成链的方式和之前所提到的两篇文章中所写的一样，将两个序列拼在一起。

三、代码

#include<bits/stdc++.h>
using namespace std;
const int N = 210;
int f[N][N];
int a[N];
int main()
{
	int n;
	cin >> n;
	for(int i = 0; i < n; i ++ )
	{
		cin >> a[i];
		a[i + n] = a[i];
	}
	for(int len = 3; len <= n + 1; len ++ )
	{
		for(int l = 0; l + len - 1 < 2 * n; l ++ )
		{
			int r = l + len - 1;
			for(int k = l + 1; k < r; k ++ )
			{
				f[l][r] = max(f[l][r], f[l][k] + f[k][r] + a[l] * a[k] * a[r]);
			}
		}
	}
	int maxv = 0;
	for(int i = 0; i + n + 1 - 1 < 2 * n; i ++ )
	{
		int r = i + n + 1 -1;
		if(maxv < f[i][r])maxv = f[i][r];
	}
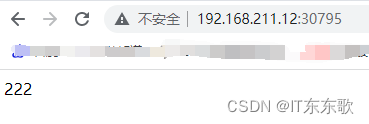
	cout << maxv << endl;
	return 0;
}