KMP（字符串匹配算法）

主串或目标串：比较长的，我们就是在它里面寻找子串是否存在；

子串或模式串：比较短的。

前缀：字符串A和B，A = B+S，S非空，则B为A的前缀。

后缀：A = S+B，S非空，则B为A的后缀。

PMT：前缀集合和后缀集合的交集中，最长前缀的长度。

部分匹配表：PMT值集合，字符串的所有前缀的PMT值。

当出现失配的字符时，我们原来的暴力算法需要将目标串逐个后移，这个过程其实就是拿已经匹配部分的前缀去逐个匹配后缀。如果我们能够知道每一个位置i处，S[0:i]中已经和后缀匹配的前缀，那么我们是不是就可以直接将前缀和后缀对齐，进而跳过了中间一些字符，然后直接去比较模式串i+1处的字符呢？答案是肯定的。

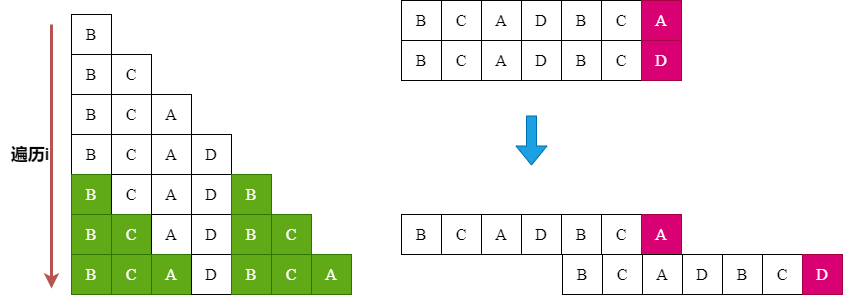
图中绿色块，就是构建next数组过程中，随着遍历的深入，前缀和后缀的匹配情况。

其实，我们换一个方向去思考或许更容易：

例如红色A处失配，那么我们就将目标串往后移动，我们希望移动到模式串的前缀和当前已经遍历到的目标串的后缀匹配字符最多的地方。

我们需要一个next数组记录目标串的当前位置失配时，模式串应该转跳的位置。

next数组与模式串对应。并且next[0] = -1，表示第一个字符没有匹配的前后缀，如果在0位置失配，只能将目标串后移一位，去和模式串的第二位进行匹配。

next数组中如果某一个元素值为-1，其实就是表示模式串当前位置没有匹配的前缀，如果在这个位置失配，那么应该直接将目标串的第一位和模式串的下一位比较。

next数组的构造，是通过模式串自己的前缀和后缀匹配进行的。

next[0]=-1;
// 初始化next数组
int i=0,j=-1;//i指向目标串，j指向模式串
while(i<ch.length){
    if(j==-1){
        // j=-1，说明，与i匹配的地方是空，那么也就说明，模式串已经到开头了
        // 但是还是和目标串不匹配
        // abab bab b和a不匹配，我们应该将i后移再和j匹配。
        i+=1;
        j+=1;
    }
    if(ch[i]==ch[j]){
        i+=1;
        j+=1;
        // 当前位置匹配，next[i]的值等于当前位置之前的字符串的PMT
        next[i]=j;
    }
    else{
        // 当前位置不匹配，对模式串进行转跳，
        // next[j]表示如果在当前位置失配，就应该将模式串的索引转跳到next[j]位置，继续匹配
        j=next[j];
    }
}

next[i]数组的值表示匹配串的i位置失配了，那么就应该拿模式串的前缀继续和当前位置匹配，即转跳到next[i]位置，继续判断是否匹配。

public static int KMP(String Str,String Sub,int pos){
    if (Str == null || Sub == null){
        return -1;
    }
    int i = pos, j = 0;
    int[] next = new int[Sub.length()];
    getNext(next,Sub);
    while(i < Str.length() && j < Sub.length()){
        if (j == -1 || Str.charAt(i) == Sub.charAt(j)){
            i++;
            j++;
        }else {
            j = next[j];
        }
    }
    if (j >= Sub.length()){
        return i-j;
    }else {
        return -1;
    }
}
public static void getNext(int[] next,String sub){
    next[0] = -1;
    next[1] = 0;
    int i = 2,k = 0;
    while(i < next.length){
        if (k ==- 1 || sub.charAt(k) == sub.charAt(i-1)){
            next[i] = k+1;
            i++;
            k++;
        }else {
            k = next[k];
        }
    }
}

示例一

459. 重复的子字符串

/**
 * 方法一：枚举法，由于子串至少有两个，因此，我们枚举子串的长度1<=k<=n//2;
 * 方法二：KMP算法，首先先证明一个原理
 * 假设s的子串为c，且为4个，那么s可以表示为     ccccc
 * 如果我们将第一个c移动到末尾，那么应该还可以组成s。
 * 基于这个原理，我们将s复制一份，变成 ss，如果我们删除ss的第一个字符和最后一个字符
 * 如果s存在子串c，那么，ss经过删除前后两个字符后，中间部分一定还存在和s匹配的字符串
 */

示例二

1392. 最长快乐前缀

/**
 * 思路：kmp算法，首先需要得到字符串s的next数组
 * 然后，根据题意可知，快乐前缀是和后缀匹配的。那么我们就需要知道，next数组中最后一个位置的数值pos
 * pos表示，s最后一个数对应的转跳位置，然后，我们需要进一步比较s[pos]是否等于s[-1]：
 *   a. 等于，则找到了最长的快乐前缀；
 *   b. 不等于，pos位置失配，继续转跳pos=next[pos];
 * 直到s[pos]==s[-1]或者pos==-1为止。
 */