JAVA中的Prim和Dijkstra问题详解

news2024/9/23 7:33:05

1.概念

Prim算法是一种计算加权无向图的最小生成树的算法。所谓最小生成树，是指一个图的子图，它包含图中所有的顶点，并且有保持图连通的最少的边，且所有边的权值之和最小。
Prim算法的基本思想是从图中任意一个顶点开始，逐渐增长最小生成树。在每一步，算法都会选择连接已选顶点和未选顶点之间权重最小的边，并将其加入到最小生成树中，同时将新加入的顶点标记为已选。这个过程一直重复，直到所有的顶点都被选中，最终形成最小生成树。

Prim算法的具体步骤如下：
1. 初始化：选择一个起始顶点v，加入到最小生成树中，并将与v相连的边和它们的权重记录下来。
2. 循环执行以下步骤，直到所有顶点都被加入最小生成树：
   a. 在所有连接已选顶点和未选顶点的边中，找到权重最小的边(u, v)，其中u是已选顶点，v是未选顶点。
   b. 将边(u, v)加入到最小生成树中，并将顶点v标记为已选。
   c. 更新与顶点v相连的边和它们的权重的记录。
3. 当所有顶点都被加入最小生成树后，算法结束，最小生成树形成。
Prim算法的时间复杂度取决于所使用的的数据结构。如果使用邻接矩阵表示图，算法的时间复杂度为O(V^2)，其中V是顶点的数量。如果使用优先队列（例如斐波那契堆）来实现，算法的时间复杂度可以降低到O(E + VlogV)，其中E是边的数量。 

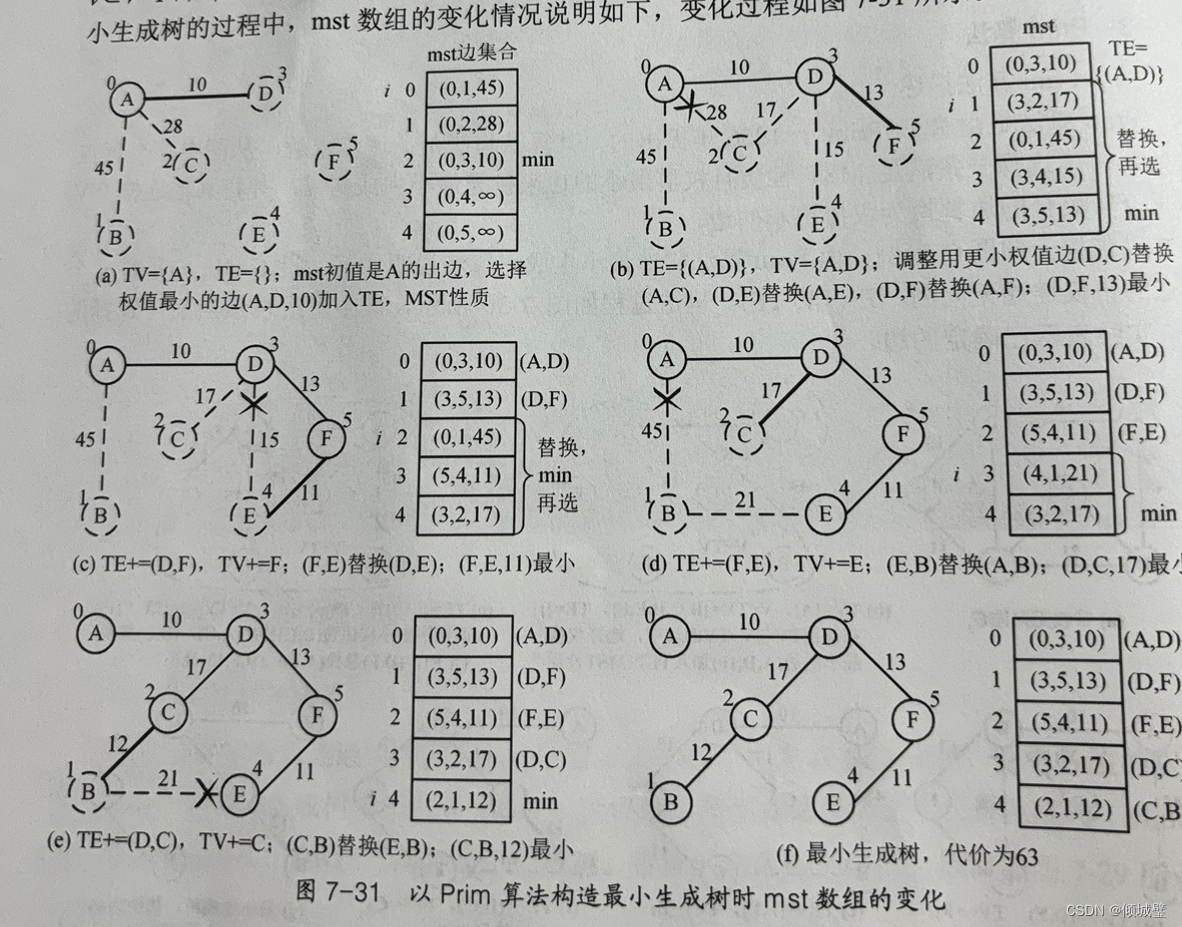
 1.最初T的顶点集合TV={A}，V-TV{B,C,D,E,F},边的集合为TE={}。

2.在所有的邻接边中，选择权值最小的边，如（A，B），（A，C），（A，D），中最小的权值边为（A，D）。不断重复这个过程，将边(u, v)加入到最小生成树中，并将顶点v标记为已选。 更新与顶点v相连的边和它们的权重的记录。 

2.Prim的算法实现

设已构造一个有n个顶点的图G，Prim算法使用一个数组mst记录G的一颗最小生成树，我们可以使用优先队列（通常是一个最小堆）来高效地选择最小边。

下面是实现Prim算法的代码

import com.sun.org.apache.bcel.internal.generic.IF_ACMPEQ;

public class prim {
    private char[] mVexs;//顶点集合
    private int[][] mMatrix;//邻接矩阵
    private static final int INF =Integer.MAX_VALUE;
    public void prim(int start){
        int num =mVexs.length;//顶点个数
        int index =0;//prim最小数的索引，即prims数组的索引
        char[] prims =new char[num];//prim最小数的结果数组
        int[] weights =new int[num];//顶点间边的权值

        //prim最小生成树中第一个数是“图中第start个顶点”，因为是从start开始的
        prims[index++]=mVexs[start];
        //初始化“顶点的权值数组”
        //将每个顶点的权值初始化为“第start个顶点”到“该顶点”的权值
        for (int i =0;i<num;i++){
            weights[i]=mMatrix[start][i];
            //将第start个顶点的权值初始化为0
            //可以理解为“第start个顶点到它自身的距离为0”
            weights[start]=0;

            for(int j =0;j<num;j++){
                //由于从start开始的，因此不需要再对第start个顶点进行处理
                if(start==j)
                    continue;

                    int i1 =0;
                    int k =0;
                    int min=INF;
                    //再未加入到最小生成树的顶点中，找出权值最小的顶点
                while(i1<num){
                    //若weight[j]=0，意味着“第i1个节点已经被排序过”
                    if(weights[i1]!=0&&weights[i1]<min){
                        min=weights[j];
                        k=i1;
                    }
                    i++;

                }
                //在经过上面的处理之后，在未加入到最小生成树的顶点中，权值最小的顶点时第k个顶点
                //将第k个顶点加入到最小生成树的结果数组中
                prims[index++]=mVexs[k];
                //将“第k个顶点的权值”标记为0，意味着第k个顶点已经排序过了
                weights[k]=0;
                //当第k个顶点被加入到最小生成树的数组中之后，更新其他的顶点权值
                for (j=0;j<num;j++){
                    //当第j个节点没有被处理，并且需要更新是才被更新
                    if (weights[j]!=0&&mMatrix[k][j]<weights[j]){
                        weights[j]=mMatrix[k][j];
                        
                    }
                }
             
                }

            }
     
        }
    }

单源最短路径

单源最短路径是指从一个顶点vi到图中其他顶点的最短路径。Dijkstra针对非负权值的带权图，提出一个按路径长度递增次序逐步求得单源最短路径的算法。通常称为Dijkstra算法。

1.Dijkstra算法描述 

Dijkstra算法思想是：逐步求解，每步将一条最短路径扩充一条边形成下一条最短路径，并将其他路径替换成更短的。

Dijktra算法描述： 

1、初始化一个距离数组dist[ ]，其中dist[i]表示从源点到定点i的当前已知最短距离。初始时，源点到自身的距离设置为0，其余定点的距离设置为无穷大。同时设置一个标记数组path来记录哪些定点的最短路径已经被确定。

2、确定最小距离顶点：从未确定最短路径的顶点集合中，选择一个具有最小dist[]值的顶点u，将其加入到已经确定最短路径的集合s中

3、更新距离：对于顶点u的每一个邻接顶点v如果通过顶点u到达个路径小于当前已知的dist[v]，则更新dist[v]为

如图所示v1-v6六个点以及他们的有向权重连线，现在我们假设从v1出发，画出从顶点v1到其余各点最短路径的过程。

该算法需要使用3个数组的定义

  1. s数组用于存储前述集合s
  2. dist数组用于保存最短路径长度
  3. path数组保存最短路径经过顶点序列
  4. v用于存储还有多少个数组没有被确认
数组s数组vdist[]path
{v1}{v2，v3，v4，v5，v6}{0,10,12,oo,oo,oo}{v1,v1,v1,-1,-1,-1}
{v1,v2}
  1.  首先，我们将v1拿出来，v1能连接v2和v3，v1到v1的距离我们可以看成0，v1到v2的距离是10，v1到v3的距离是12。
  2. v1不能直接到达v4，v5，v6，我们可以看成无穷大，那么v1的上一个节点是v1，但是v4，v5，v6目前还没有连接到节点就记录为-1.
  3. 然后我们根据数组{0,10,12,oo,oo,oo}，找到数组的最小值，即v2的10，我们将v2加入到数组s中
数组s数组vdist[]path
{v1}{v2，v3，v4，v5，v6}{0,10,12,oo,oo,oo}{v1,v1,v1,-1,-1,-1}
{v1,v2}{v3,v4,v5,v6}{0,10,12,26,35,oo}{v1,v1,v1,v2,v2,-1}
{v1,v2,v3}
  1. 我们从距离数组中{0,10,12,26,35,oo}，选取最小值，即v3节点加入数组s中，数组v为{v4，v5，v6}。
  2. 现在有另一个路线为v1-v3-v2,但是长度为15比10大，所以不做变化，v1到v3的距离还是12，所以v3的上一个节点还是v1。
  3. v4和v5是可以根据v2进行跟进的，v4 =10+16=26，v5 =10 +15 =35。

 

数组s数组vdist[]path
{v1}{v2,v3,v4,v5,v6}{0,10,12,oo,oo,oo}{v1,v1,v1,-1,-1,-1}
{v1,v2}{v3,v4,v5,v6}{0,10,12,26,35,oo}{v1,v1,v1,v2,v2,-1}
{v1,v2,v3}{v4,v5,v6}{0,10,12,24,35,20}{v1,v1,v1,v3,v2,v3}
{v1,v2,v3,v6}{v4,v5}
  1. 我们在数组中{0,10,12,24,35,20}可以看出在去掉v1,v2,v3之后的最小点是v6，我们将v6加入到数组当中， 所以我们将v6加入到数组s中，v1到v1，v2，v3的距离保持不变。
  2. v1到v4的路径，多了个v6，所以多出来了个路径v1-v3-v6-v4，距离是22，比之前的24小，进行更新，所以v4的上一个节点变成了v6。
  3. 然后v1到v5，多增加了路线了，v1-v3-v6-v5,距离变成了30，比之前的35要小，更新表格，v5的上一个节点变成v6。

 

数组s数组vdist[]path
{v1}{v2,v3,v4,v5,v6}{0,10,12,oo,oo,oo}{v1,v1,v1,-1,-1,-1}
{v1,v2}{v3,v4,v5,v6}{0,10,12,26,35,oo}{v1,v1,v1,v2,v2,-1}
{v1,v2,v3}{v4,v5,v6}{0,10,12,24,35,20}{v1,v1,v1,v3,v2,v3}
{v1,v2,v3,v6}{v4,v5}{0,10,12,22,30,20}{v1,v1,v1,v6,v6,v3}
{v1,v2,v3,v6,v4}          {v5}

从数组v中取出距离最短的值v4放入数组s中，此时v1到v1，v2，v3，v4的距离保持不变，v1-v5的距离多出一条v1-v3-v6-v4-v5，路径29比之前的30要短，更新表格，所以v5的上一个节点是v4。

数组s数组vdist[]path
{v1}{v2,v3,v4,v5,v6}{0,10,12,oo,oo,oo}{v1,v1,v1,-1,-1,-1}
{v1,v2}{v3,v4,v5,v6}{0,10,12,26,35,oo}{v1,v1,v1,v2,v2,-1}
{v1,v2,v3}{v4,v5,v6}{0,10,12,24,35,20}{v1,v1,v1,v3,v2,v3}
{v1,v2,v3,v6}{v4,v5}{0,10,12,22,30,20}{v1,v1,v1,v6,v6,v3}
{v1,v2,v3,v6,v4}          {v5}{0,10,12,22,30,20}{v1,v1,v1,v6.v4.v3}
{v1,v2,v3,v6,v4,v5}{}{0,10,12,22,30,20}{v1,v1,v1,v6.v4.v3}
public class Dijkstra {
    private Queue visited;
    int[] distance;

    public Dijkstra(int len) {
        // TODO Auto-generated constructor stub
        visited = new LinkedList();
        distance = new int[len];

    }

    private int getIndex(Queue q, int[] dis) {
        int k = -1;
        int min_num = Integer.MAX_VALUE;
        for (int i = 0; i < dis.length; i++) {
            if (!q.contains(i)) {
                if (dis[i] < min_num) {
                    min_num = dis[i];
                    k = i;
                }
            }
        }
        return k;
    }

    public void dijkstra(int[][] weight, Object[] str, int v) {
        HashMap path;
        path = new HashMap();
        for (int i = 0; i < str.length; i++)
            path.put(i, "");

        //初始化路径长度数组distance
        for (int i = 0; i < str.length; i++) {
            path.put(i, path.get(i) + "" + str[v]);
            if (i == v)
                distance[i] = 0;
            else if (weight[v][i] != -1) {
                distance[i] = weight[v][i];
                path.put(i, path.get(i) + "-->" + str[i]);
            } else
                distance[i] = Integer.MAX_VALUE;
        }
        visited.add(v);
        while (visited.size() < str.length) {
            int k = getIndex(visited, distance);//获取未访问点中距离源点最近的点
            visited.add(k);
            if (k != -1) {

                for (int j = 0; j < str.length; j++) {
                    //判断k点能够直接到达的点
                    if (weight[k][j] != -1) {
                        //通过遍历各点，比较是否有比当前更短的路径，有的话，则更新distance，并更新path。
                        if (distance[j] > distance[k] + weight[k][j]) {
                            distance[j] = distance[k] + weight[k][j];
                            path.put(j, path.get(k) + "-->" + str[j]);
                        }
                    }

                }
            }
        }
        for (int h = 0; h < str.length; h++) {
            System.out.printf(str[v] + "-->" + str[h] + ":" + distance[h] + " ");
            if (distance[h] == Integer.MAX_VALUE)
                System.out.print(str[v] + "-->" + str[h] + "之间没有可通行路径");
            else
                System.out.print(str[v] + "-" + str[h] + "之间有最短路径，具体路径为：" + path.get(h).toString());
            System.out.println();
        }
        visited.clear();

    }
public static void main(String[] args) {
        // TODO Auto-generated method stub
        int[][] weight = {
                {0, 10, 12, -1, -1, -1},
                {-1, 0, -1, 16, 25, -1},
                {4, 3, 0, 12, -1, 8},
                {-1, -1, -1, 0, 7, -1},
                {-1, -1, -1, -1, 0, -1},
                {-1, -1, -1, 2, -1, 0}};
        String[] str = {"V1", "V2", "V3", "V4", "V5", "V6"};
        int len = str.length;
        Dijkstra dijkstra = new Dijkstra(len);
        //依次让各点当源点，并调用dijkstra函数
        for (int i = 0; i < str.length; i++) {
            dijkstra.dijkstra(weight, str, i);
        }
    }

}

运行结果：

V1-->V1:0 V1-V1之间有最短路径，具体路径为：V1
V1-->V2:10 V1-V2之间有最短路径，具体路径为：V1-->V2
V1-->V3:12 V1-V3之间有最短路径，具体路径为：V1-->V3
V1-->V4:22 V1-V4之间有最短路径，具体路径为：V1-->V3-->V6-->V4
V1-->V5:29 V1-V5之间有最短路径，具体路径为：V1-->V3-->V6-->V4-->V5
V1-->V6:20 V1-V6之间有最短路径，具体路径为：V1-->V3-->V6
V2-->V1:2147483647 V2-->V1之间没有可通行路径
V2-->V2:0 V2-V2之间有最短路径，具体路径为：V2
V2-->V3:2147483647 V2-->V3之间没有可通行路径
V2-->V4:16 V2-V4之间有最短路径，具体路径为：V2-->V4
V2-->V5:23 V2-V5之间有最短路径，具体路径为：V2-->V4-->V5
V2-->V6:2147483647 V2-->V6之间没有可通行路径
V3-->V1:4 V3-V1之间有最短路径，具体路径为：V3-->V1
V3-->V2:3 V3-V2之间有最短路径，具体路径为：V3-->V2
V3-->V3:0 V3-V3之间有最短路径，具体路径为：V3
V3-->V4:10 V3-V4之间有最短路径，具体路径为：V3-->V6-->V4
V3-->V5:17 V3-V5之间有最短路径，具体路径为：V3-->V6-->V4-->V5
V3-->V6:8 V3-V6之间有最短路径，具体路径为：V3-->V6
V4-->V1:2147483647 V4-->V1之间没有可通行路径
V4-->V2:2147483647 V4-->V2之间没有可通行路径
V4-->V3:2147483647 V4-->V3之间没有可通行路径
V4-->V4:0 V4-V4之间有最短路径，具体路径为：V4
V4-->V5:7 V4-V5之间有最短路径，具体路径为：V4-->V5
V4-->V6:2147483647 V4-->V6之间没有可通行路径
V5-->V1:2147483647 V5-->V1之间没有可通行路径
V5-->V2:2147483647 V5-->V2之间没有可通行路径
V5-->V3:2147483647 V5-->V3之间没有可通行路径
V5-->V4:2147483647 V5-->V4之间没有可通行路径
V5-->V5:0 V5-V5之间有最短路径，具体路径为：V5
V5-->V6:2147483647 V5-->V6之间没有可通行路径
V6-->V1:2147483647 V6-->V1之间没有可通行路径
V6-->V2:2147483647 V6-->V2之间没有可通行路径
V6-->V3:2147483647 V6-->V3之间没有可通行路径
V6-->V4:2 V6-V4之间有最短路径，具体路径为：V6-->V4
V6-->V5:9 V6-V5之间有最短路径，具体路径为：V6-->V4-->V5
V6-->V6:0 V6-V6之间有最短路径，具体路径为：V6

Process finished with exit code 0

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1929979.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Go Web开发框架之Gin

Go Web开发框架之Gin

&#x1f49d;&#x1f49d;&#x1f49d;欢迎莅临我的博客&#xff0c;很高兴能够在这里和您见面&#xff01;希望您在这里可以感受到一份轻松愉快的氛围&#xff0c;不仅可以获得有趣的内容和知识&#xff0c;也可以畅所欲言、分享您的想法和见解。 推荐:「stormsha的主页」…
阅读更多...
【香橙派AiPro】基于VGG16的火灾检测模型预测

【香橙派AiPro】基于VGG16的火灾检测模型预测

目录 引言开发板介绍开发板使用准备工作工具文档 拨码开关镜像烧录连接开发板下载MobaXterm网线-SSH连接开发板设置WIFI连接WIFI-SSH连接开发板确定开发板IP方法 Vnc可视化WindowsiPad 开发工具安装 散热风扇基于VGG16的火灾检测模型预测数据集准备目录结构代码操作 安装宝塔最…
阅读更多...
pico+unity手柄和摄像机控制初级设置

pico+unity手柄和摄像机控制初级设置

1、摄像头配置 摄像头模式、floor是追踪原点类型&#xff08;将根据设备检测到地面的高度来计算追踪原点&#xff09;&#xff0c; Device 模式时&#xff0c;为通常理解的 Eye 模式&#xff0c;不会将根据设备检测到地面的高度来计算追踪原点 选择floor时&#xff0c;修改相…
阅读更多...
UE4-初见虚幻引擎

UE4-初见虚幻引擎

一.创建自己的工程 1.启动 a.通过桌面双击图标来打开对应版本的虚幻引擎 b.通过EPIC启动器开启动虚幻引擎 2.选择或新建项目 ps:高版本虚幻编辑器可以打开低版本的虚幻项目&#xff0c;但是高版本虚幻的项目不可以由低版本的虚幻编辑器打开。 3. 选择要打开的项目 4.选择模版 选…
阅读更多...
Linux桌面环境手动编译安装librime、librime-lua以及ibus-rime，提升中文输入法体验

Linux桌面环境手动编译安装librime、librime-lua以及ibus-rime，提升中文输入法体验

Linux上的输入法有很多&#xff0c;大体都使用了Fcitx或者iBus作为输入法的引擎。相当于有了一个很不错的“地基”&#xff0c;你可以在这个“地基”上盖上自己的“小别墅”。而rime输入法&#xff0c;就是一个“毛坯别墅”&#xff0c;你可以在rime的基础上&#xff0c;再装修…
阅读更多...
Win10+Docker环境使用YOLOv8 TensorRT推理加速

Win10+Docker环境使用YOLOv8 TensorRT推理加速

这一部分内容和WSL-Ubuntu20.04环境使用YOLOv8 TensorRT推理加速-CSDN博客 是基本相同的，有细微差别我也会在文中指出来。 1.TensorRTX下载 这里使用Wang-xinyu大佬维护的TensorRTX库来对YOLOv8进行推理加速的演示，顺便也验证一下前面环境配置的成果。 github地址：GitHub -…
阅读更多...
windows10 背景如何变成护眼淡绿色

windows10 背景如何变成护眼淡绿色

windows10 背景如何变成护眼淡绿色&#xff0c;office、输入窗口、网页前景、通讯软件光标全是变绿&#xff0c;保护色。 1、运行窗口输入 regedit 2、计算机\HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\Windows\CurrentVersion\Themes\DefaultColors\Standard 侧面的window名称数…
阅读更多...
浏览器确定是否停留在当前Tab页面

浏览器确定是否停留在当前Tab页面

切换页面时打印页面状态如图&#xff1a; 这里用到了visibilitychange事件。 document.addEventListener(visibilitychange,function(){console.log(document.visibilityState)})
阅读更多...
Vue和Element UI 路由跳转

Vue和Element UI 路由跳转

在Vue.js中&#xff0c;使用Vue Router可以方便地实现页面之间的路由跳转。Element UI是一个基于Vue 2.0的桌面端组件库&#xff0c;它本身并不直接提供路由跳转的功能&#xff0c;但你可以在使用Element UI的Vue项目中结合Vue Router来实现这一功能。 以下是一个基于Vue和Ele…
阅读更多...
JavaScript进阶（四）---js解构

JavaScript进阶（四）---js解构

目录 一.定义&#xff1a; 二.类型&#xff1a; 1.数组解构&#xff1a; 1.1变量和值不匹配的情况 1.2多维数组 2.对象解构 3.对象数组解构 4.函数参数解构 5.扩展运算符 一.定义&#xff1a; JavaScript 中的解构&#xff08;Destructuring&#xff09;是一种语法糖&…
阅读更多...
基于Ubuntu2310搭建openstack高可用集群B版

基于Ubuntu2310搭建openstack高可用集群B版

openstack-ha 环境初始化安装haproxy安装keepalived数据库集群高可用rabbitmq集群高可用memcache集群配置 keystone高可用glance高可用placement高可用nova高可用neutron高可用horizon高可用 本实验使用两台节点master和node配置haproxy高可用&#xff0c;keepliaved配置主备抢…
阅读更多...
H5 Svg 半圆圆环占比图

H5 Svg 半圆圆环占比图

效果图 主逻辑 /* 虚线长度 */ stroke-dasharray /* 偏移 */ stroke-dashoffset 代码 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge&qu…
阅读更多...
sentinel网关限流配置及使用

sentinel网关限流配置及使用

sentinel控制台源码&#xff1a;https://download.csdn.net/download/yixin605691235/89543923 sentinel控制台jar包&#xff1a;https://download.csdn.net/download/yixin605691235/89543931 不同环境直接修改jar包中的application.yml文件中的nacos地址就可以了。 一、网关限…
阅读更多...
socket功能定义和一般模型

socket功能定义和一般模型

1. socket的功能定义 socket是为了使两个应用程序间进行数据交换而存在的一种技术&#xff0c;不仅可以使同一个主机上两个应用程序间可以交换数据&#xff0c;而且可以使网络上的不同主机间上的应用程序间进行通信。 2. 图解socket的服务端/客户端模型
阅读更多...
MySQL面试篇章——MySQL基础复习

MySQL面试篇章——MySQL基础复习

文章目录 MySQL基本介绍MySQL数据类型数值类型字符串类型日期和时间类型ENUM和SET MySQL运算符算数运算符逻辑运算符比较运算符 MySQL常用函数字符串函数数值函数时间和日期函数聚合函数 MySQL完整性约束范式第一范式&#xff08;1NF&#xff09;第二范式&#xff08;2NF&#…
阅读更多...
＜数据集＞钢铁缺陷检测数据集＜目标检测＞

＜数据集＞钢铁缺陷检测数据集＜目标检测＞

数据集格式&#xff1a;VOCYOLO格式 图片数量&#xff1a;1800张 标注数量(xml文件个数)&#xff1a;1800 标注数量(txt文件个数)&#xff1a;1800 标注类别数&#xff1a;6 标注类别名称&#xff1a;[crazing, patches, inclusion, pitted_surface, rolled-in_scale, scr…
阅读更多...
【C语言】详解结构体（上）

【C语言】详解结构体（上）

文章目录 前言1. 结构体类型的含义2.结构体的声明2.1 结构体声明的语法2.2 结构体变量的创建和初始化 3.结构体的特殊声明4. 结构体的自引用5.小结 前言 C语言的数据类型分为内置数据类型和自定义的数据类型。所谓的内置的数据类型可以认为是C语言自带的数据类型&#xff08;c…
阅读更多...
three完全开源扩展案例03-模型加载

three完全开源扩展案例03-模型加载

https://www.threelab.cn/three-cesium-examples/public/index.html#/codeMirror?navigationThree.js%E6%A1%88%E4%BE%8B[r166]&classifybasic&idmodelLoad 更多内容&#xff1a;https://threelab.cn/ import * as THREE from three import { OrbitControls } from …
阅读更多...
AI+折叠屏，荣耀的创新周期论

AI+折叠屏，荣耀的创新周期论

文&#xff5c;刘俊宏 编&#xff5c;王一粟 2024年&#xff0c;AI和折叠屏的演进路线&#xff0c;已经成为了手机行业的共识。 首先&#xff0c;手机市场的新增量已经被折叠屏所接管。据Counterpoint Research数据显示&#xff0c;中国2024年第一季度折叠屏手机销量同比增长…
阅读更多...
最新Qt6的下载与成功安装详细介绍

最新Qt6的下载与成功安装详细介绍

引言 Qt6 是一款强大的跨平台应用程序开发框架&#xff0c;支持多种编程语言&#xff0c;最常用的是C。Qt6带来了许多改进和新功能&#xff0c;包括对C17的支持、增强的QML和UI技术、新的图形架构&#xff0c;以及构建系统方面的革新。本文将指导你如何在Windows平台上下载和安…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023