没有白走的路,每一步都算数🎈🎈🎈
题目描述:
已知一个4x4的方格,和一个16个单位长度组成的玩具蛇,即蛇头,蛇身,蛇尾的长度总共是16,
假设蛇的一节在方格中的位置有一点的不一样,也就是有一个不同的摆法。求总共有多少种方法?
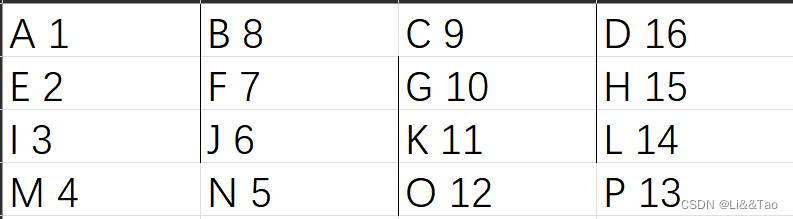
一种摆法
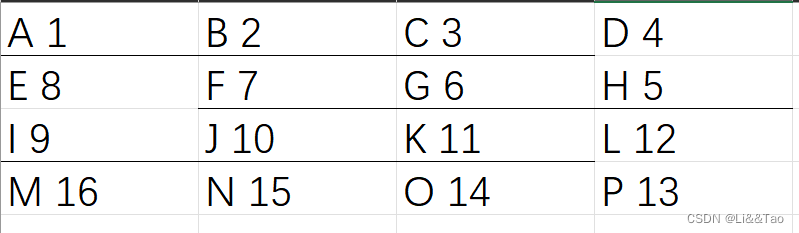
一种摆法
其中1,2,3,4,...16表示蛇的每个小结点
输入描述:
程序没有输入的数据
输出描述:
输出在上述方格种玩具蛇可以摆置的方案数
算法分析:
在之前刷过的题目当中,已经做过很多的dfs的题目,但是都不是完全熟练。
还好这道题目,给我一个手写dfs的机会,难得。写代码的过程特别的舒服,很开心。
数据定义:
- mp数组 用来判定位置是否被使用,初始值都设置为0
- d数组 为上一个递归位置和下一个递归位置搭建桥梁[[1,0],[-1,0],[0,1],[0,-1]]
- ans 变量,定义为全局变量,用来计算所有可行的方案数。初始值设置为0
初步算法设计分析:
- 因为有16个格子,所以对16个格子都可以先设置为1
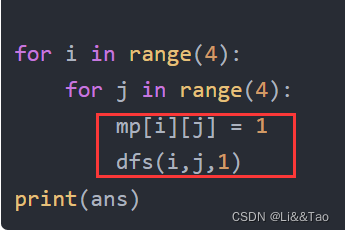
当时好像连这个双重for循环都紧张的不会写了。
- 编写dfs函数
第一步:
是编写for循环,if条件语句,用来dfs出下一个dfs的坐标
第二步:
是编写dfs程序结束的条件,当cnt等于16的时候,就结束,同时ans+=1,ans的值增加1。
同时程序return,return可以返回任何整数值。
第三步:
检验递归,即把mp的值设置成1,或者其他任何非0值都行
如果不设置map的值,你的风扇估计会转。
可以试试这个代码
import os
import sys
sys.setrecursionlimit(10000)
mp = [[0]*4 for i in range(4)]
d = [[1,0],[-1,0],[0,1],[0,-1]]
ans = 0
def dfs(x,y,cnt):
global ans
if cnt==16:
ans += 1
return
for i in range(4):
nx = x+d[i][0]
ny = y+d[i][1]
if 0<=nx<=3 and 0<=ny<=3:
if mp[nx][ny]==0:
## mp[nx][ny]=1
dfs(nx,ny,cnt+1)
## mp[nx][ny] = 0
## mp[x][y] = 0
for i in range(4):
for j in range(4):
mp[i][j] = 1
dfs(i,j,1)
print(ans)AC算法
import os
import sys
sys.setrecursionlimit(10000)
mp = [[0]*4 for i in range(4)]
d = [[1,0],[-1,0],[0,1],[0,-1]]
ans = 0
def dfs(x,y,cnt):
global ans,mp
if cnt==16:
ans += 1
return 1
for i in range(4):
nx = x+d[i][0]
ny = y+d[i][1]
if 0<=nx<=3 and 0<=ny<=3:
if mp[nx][ny]==0:
mp[nx][ny]=1
dfs(nx,ny,cnt+1)
mp[nx][ny] = 0
mp[x][y] = 0
for i in range(4):
for j in range(4):
mp[i][j] = 1
dfs(i,j,1)
print(ans)
每日一句
摘自《《晚熟的人》》:
不要太在意别人怎么在背后议论你,比不上你,只是在背后说你,比你强,人家忙着赶路,没时间理你。