给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
示例 1:
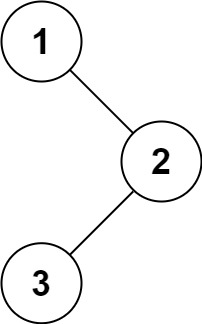
输入:root = [1,null,2,3] 输出:[1,2,3]
示例 2:
输入:root = [] 输出:[]
示例 3:
输入:root = [1] 输出:[1]
示例 4:
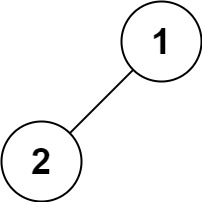
输入:root = [1,2] 输出:[1,2]
示例 5:
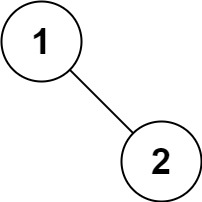
输入:root = [1,null,2] 输出:[1,2]
提示:
- 树中节点数目在范围
[0, 100]内 -100 <= Node.val <= 100
【方法一】递归算法
二叉树的先序遍历按照:根-左-右来进行。
针对主函数,我们需要定义一个数组a,将遍历的树中元素放在数组中;returnSize指针所指向的值初始化为0,表示结果数组的大小初始为0;调用preorder函数,返回数组a。
针对调用函数,首先进行判断是否为空,为空的话直接进行返回,不需要进行任何操作。然后按照根-左-右来进行遍历。针对根节点处理:a[(*returnSize)++] = root->val。将根节点保持到数组中,然后将returnSize+1,进行下一个节点操作。
具体案例分析:
root = [1,null,2,3],输出:[1,2,3]。
针对主函数,开始时a[0]={},returnSize=0,然后调用preorder(root, a, returnSize)。
由于 root 不为空,访问 root->val,即1,将其添加到数组 a[0],并将 *returnSize 递增为1。然后递归调用 preorder(root->left, a, returnSize),但 root->left 为空,因此直接返回。
递归调用 preorder(root->right, a, returnSize)。
同样地,由于 root->right->val不为空,访问 root->val,即2,将其添加到数组 a[1],并将 *returnSize 递增为1。继续递归调用preorder(root->left, a, returnSize)。
进入左子树后,此时的root->left->val不为空,访问 root->val,即3,将其添加到数组 a[2],并将 *returnSize 递增为1。然后继续preorder(root->left, a, returnSize)和preorder(root->right, a, returnSize)。为空返回到上一层,进行调用root=2的右子树,preorder(root->right, a, returnSize)。为空,直接返回。
最终,数组 a 包含元素 [1, 2, 3],并且 *returnSize 为3。
返回数组 a。
(整个流程可以描述为,root=1->返回1->preorder(root->left, a, returnSize)为空->调用preorder(root->right, a, returnSize)进入右子树,此时root=2->返回2->调用preorder(root->left, a, returnSize)进入左子树,此时root=3->返回3->preorder(root->left, a, returnSize)和preorder(root->right, a, returnSize)为空,返回到根为2的这一层,调用preorder(root->right, a, returnSize)为空。循环和调用结束。返回a[1,2,3])
C语言具体代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
void preorder(struct TreeNode* root, int* a, int *returnSize){
if(!root)
return ;
a[(*returnSize)++] = root->val;
preorder(root->left,a, returnSize);
preorder(root->right, a, returnSize);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
*returnSize = 0;
int *a = (int*)malloc(sizeof(int)*100);
preorder(root,a,returnSize);
return a;
}时间复杂度O(n);空间复杂度O(n)
【方法二】非递归算法
二叉树的中序遍历按照:根-左-右来进行
非递归通过栈来进行模拟。
第一步:创建一个栈。
第二步:定义一个stack来开辟一个栈空间。并将栈初始化,top=0。定义一个数组,用来返回最后中序遍历后的树,returnSize指针所指向的值初始化为0,定义一个移动指针p指向树的根,用来遍历树。
第三步:树不为空的时候 ,入栈,然后将栈中的元素给数组,并向左遍历。左子树为空的时候,将p指针向下移动,并向右遍历树。最后返回数组a。
具体案例分析:
root = [1,null,2,3],输出:[1,2,3]。
开始时p指向root,也就是1,不为空,执行if(p != NULL)中的语句,将1进行入栈,将top++,也就是等于1,然后将栈中的元素给数组a,并将(*returnSize)++,此时returnSize=1。遍历左子树,此时为空,执行else中的语句,首先是p = stack->s[(stack->top) - 1](此时p=stack->[0]=1,也就是将p指针移回到1),然后(stack->top)--(也就是stack->top=0),下一句是 p = p->right(也就是2),开始遍历1的右子树。
此时p=2,不为空,执行if(p != NULL)中的语句,将2进行入栈,将top++,也就是等于1,然后将栈中的元素给数组a,并将(*returnSize)++,此时returnSize=2。然后继续向左遍历。此时p=3,不为空,执行if(p != NULL)中的语句,将3进行入栈,将top++,也就是等于2,然后将栈中的元素给数组a,并将(*returnSize)++,此时returnSize=3。然后继续向左遍历,为空,则进行else语句的执行。
首先是p = stack->s[(stack->top) - 1](此时p=stack->[1]=3,也就是将p指针移回到3),然后(stack->top)--(也就是stack->top=1),下一句是 p = p->right,为空,继续进入else语句的执行。首先是p = stack->s[(stack->top) - 1](此时p=stack->[0]=2,也就是将p指针移回到2),然后(stack->top)--(也就是stack->top=0),下一句是 p = p->right,为空,此时不符合while循环,跳出。结束。最后返回a=[1,2,3]。
C语言具体代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
// 创建栈
struct stack {
struct TreeNode *s[100];
int top;
};
// 先序遍历函数
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
// 开辟一个栈空间
struct stack *stack = (struct stack *)malloc(sizeof(struct stack));
// 初始化
stack->top = 0;
// 定义一个数组,用来返回最后先序遍历后的树
int *a = (int *)malloc(sizeof(int) * 100);
// returnSize指针所指向的值初始化为0
*returnSize = 0;
struct TreeNode *p = root; // 定义一个移动指针指向树的根,用来遍历树
while (p != NULL || (stack->top) != 0) { // 树不为空或者栈不为空的时候,进行入栈和出栈操作
if (p != NULL) { // 树不为空的时候 ,向左遍历。并入栈
stack->s[stack->top] = p;
(stack->top)++;
a[(*returnSize)++] = p->val; // 访问当前节点
p = p->left;
} else {
// 左子树为空,右进行遍历右字树
p = stack->s[(stack->top) - 1];
(stack->top)--;
p = p->right;
}
}
return a;
}时间复杂度O(n);空间复杂度O(h)