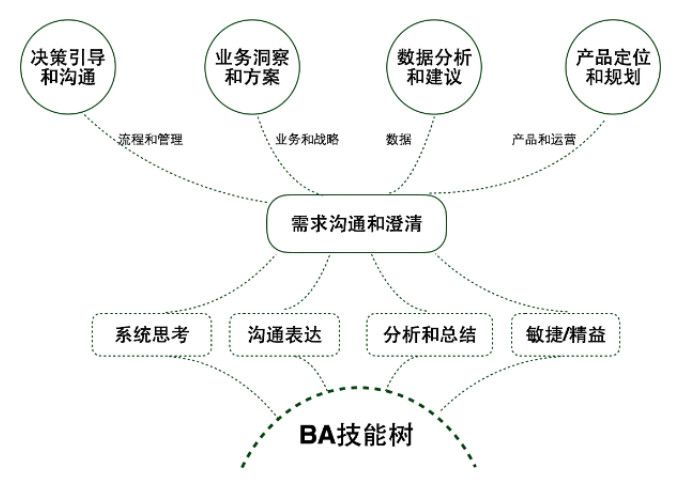
Numpy是Python科学计算库的基础,主要包括:
- 强大的N维数组对象和向量运算。
- 一些复杂的功能。
- 与C++和FORTRAN代码的集成。
- 实用的线性代数运算、傅里叶变换、随机数生成等。
9.1 Numpy基础
Numpy的主要对象是一个均匀的多维数组。Numpy提供了各种函数。可以非常方便、灵活地操作数组,熟练掌握数组的基本概念是使用数组这种数据结构的基本要求。
9.1.1 数组对象介绍
如下图所示,可以通过下标对数组内的数据进行索引取值。

在Numpy中,方向称作轴,轴的数目称作维。比如,3D空间内的一点坐标是(1,1,0),在Numpy中是一个一维数组,因为它只有一个轴。在比如:
array([1,1,1],
[0.0.0])这个数组有两个方向,有两个轴,所以是一个二维数组。
N维数组在Numpy中是一个ndarray类,也可以叫做array。不要把Numpy中的array和Python标准库中的array混淆,Python标准库中的array只处理一维数组,且只提供少量的函数。ndarray类比较重要的属性有以下几个。
1.ndarray.ndim
数组的纬度,如下图:

2.ndarray.shape
数组的形状。返回一个元组,表示数组在各个方向上的长度。比如一个n行m列的矩阵,shape值会是(n,m)。返回的元组的长度等于数组的纬度,如下图:

3.ndarray.size
数组的大小。这个值等于shape元组内各个元素的乘积,如下图:

4.ndarray.dtype
数组内元组的数据类型。可以使用Python的标准数据类型,Numpy也提供了常用的数据类型。
5.ndarry.itemsize
数组内的元素占计算机内存的大小。比如,一个float64类型的数据在计算机内占8bit的内存空间。
6.ndarray.data
数组在内存中的地址。一般通过索引操作元素,所以很少用到这个属性。
9.1.2 生成数组
生成数组的方式多种多样,比较常用的是使用Python列表、元组或者其他有序数据结构作为array()函数的参数来生成数组。Numpy会根据元素来推测合适的数组数据类型,如下图:

初学者在使用array()函数生成数组时,直接在括号内输入一系列数字,而不是使用列表等作为输入参数,如下:

array()函数回把序列的序列转换成二维数组,序列内嵌套序列的序列会生成三维数组,以此类推,如下:

也可以在array()函数内显式地声明数组的数据类型,如下:

实际中经常已知数组的大小,但是不知道数组内元素的值。因此,Numpy提供了其它生成数组的方法,数组内的数据只是用来占位的,后面有需要可以更新。
比如,zero()函数用于生成元素全为0的数组,ones()函数用于生成元素全为1的数组,empty()函数用于生成随机数组。在默认情况下,使用这些函数生成的数组的数据类型是float64。zero()函数的输入参数如果是一个整数,则会生成一维数组;如果是一个序列,则会生成多维数组,如下图:

ones()函数的使用方法和zeros()类似,如下图:

empty()函数会根据系统的状态,随机生成一些占位的元素,如下图:

注意:使用empty()函数生成的数组完全是随机的,不要试图假设生成的数组元素的值。
Numpy提供了一个与Python内建函数range()类似的arange()函数,其输入参数包括初始值、终止值、间隔值,可以生成一维的有序数组。
如果只输入一个参数,则默认的初始值是0,间隔值为1,如下图:

如果提供两个参数,则第一个参数作为初始值,第二个参数作为终止值,默认间隔值为1,如下图:

如果提供三个参数,则三个输入值依次对应初始值、终止值、间隔值,如下图:

注意:在三种情况下,输出数组的元素都没有包括终止值
当arrange()函数用于浮点数的时候,由于浮点数有限的精度,所以很难预测所生成数组的大小。Numpy提供了linspace()函数,该函数可以指定生成数组的大小,在指定的区间内生成均匀的数组,其中第一个参数为初始值,第二个参数为终止值,第三个参数为数组的大小,默认值是50,如下图:

Numpy()提供了rand()函数用于生成元素在[0,1)区间上均匀分布的数组,输入参数是数组在各个维度上的长度,如下图:

注意:以上函数生成的数组,元素的默认数据类型是float64.
常用的生成数组的函数如下表:

9.1.3 数组对象类型
Python在编写程序的时候,不需要像C/C++那样声明变量的数据类型,但是对于科学计算而言,对数据类型的控制有时候是必须的。Numpy提供了新的24种基本的数值数据类型,且大都基于C语言数据类型的命名方式:


可以使用ndrray类的astype()方法转换数组的数据类型,如下图,另外说明astype()方法首先复制原数组,然后转换数组的数据类型,并返回新的数组,所以原数组的数据类型并没有发生改变,如下图:

9.1.4 打印数组
Numpy以列表嵌套的形式打印数组,如下图,但有自动分层的特点。
最后一个轴,由左向右
倒数第二个轴,从上到下
剩下的轴从上到下,并用空行隔开
比如,一维数组以行的形式打印,二维数组以矩阵的形式打印,三维数组以嵌套矩阵的形式打印,如下图:

9.2 数组的基本操作
数组的操作非常灵活,不仅允许数组与数组之间的运算,如下图,还允许数组与某一个数字之间的运算,如下图,在进行算术运算的时候,Numpy会创建一个新的数组,并把结果写入这个新的数组中。

数组中有+=、/=运算符,这类运算符并不会创建一个新的数组,而是直接对原来的数组的元素进行修改,如下图所示。
这类运算符初学者容易误用,比如a数组元素的数据类型是整型树,b数组元素的数据类型是浮点数。假设a/b数组相加,并把值赋给a数组,这时会引发异常,如下图:

现在假设a,b数组相加,并把值赋给b数组,来看会出现什么结果,如下图:

为什么第二种方法会得到正确的结果呢?
因为a/b数组相加,Numpy会首先把a数组元素转换成与b数组元素相同的数据类型。这里有一个转换原则,就是向精度更高的数据类型转换。a/b数组相加后,得到的数组元素的数据类型是浮点数。a数组元素的数据类型是整型数,Numpy不会把精度高的数转换成精度低的数,所以会引发异常;而b数组元素的数据类型本身就是浮点数,所以可以把运算结果赋给b数组。
9.3 基本的分片和索引操作
数组可以进行分片和索引操作,从而可以非常方便地提取数组的子集或者某个元素。一维数组可以进行索引、分片、迭代等操作,和对列表的操作方式相似,如下图:

数组经过分片后,得到的数组仍然指向原数组,并没有生成一个新的数组。
比如,为分片后的数组重新赋值,原数组的值也会改变,如下图所示。之所以不直接生成一个新的数组,主要是为了节约内存资源。

多维数组的索引、分片操作更为丰富,难度也更大。多维数组的取值操作和一维数组的取值操作有所不同,如下图所示。二维数组可以看作一张表,行、列的起始位置都是0,如下图所示:

在二维数组中,要对某个元素进行索引,需要在两个轴向上定位元素,如下图:
比如,现在需要取出15这个元素,有两种方式,如下图所示:

三维数组的取值操作与二维数组类似。要取出某一个元素,必须要在三个轴向上定位;如果只在一个轴向上定位,则会得到一个二维数组,如下图:
这里得到的是一个3*3的二维数组。可以把一个数赋给取出的这个二维数组,这个数字会自动拓展这个二维数组的所有元素;也可以把形状完全一样的二维数组赋给它,如下图所示:

首先复制a[0]的原始值并赋值给old_value变量,并把9赋给a[0].
再把old_value变量中保存的二维数组赋给a[0],使得a变回最初的值,如下图所示:
和一维数组一样,多维数组也可以进行分片操作,如下图所示:

从上面几个分片操作可以看出,对多维数组进行分片操作,需要分别定义各个轴上的分片范围。
注意:方括号内从左向右以此0轴、1轴......,参考图10-38。
如果要对整个轴进行切片,则可以只使用一个冒号,如图10-45所示。

除以上分片方式外,还可以使用负值分片,如下图:

基本语法是a[i:j:k],如果i、j和表示的索引位置与n+i、n+j值表示的索引位置是一样的。
注意:n表示进行分片操作的这个轴的长度。
k<0表示从大到小反向分片。再来看下上面这个例子,i<0,那么i就被解释成7;k=-2,会依次取出索引值为7、5的元素。所以,分片结果是:
array([7,5])
Newaxis对象可以在分片操作中新建一个长度为1的轴,如下图:

9.4 高级索引
当方括号内的索引方式不再是之前介绍的简单序列的时候,就会触发高级索引。高级索引包括整数索引和布尔索引。
注意:与常规索引不同的是,高级索引会复制原数据,并返回一个新的数组。
9.4.1 整数索引
对于一维数组而言,使用数组进行索引,返回的结果和索引数组的形状一样,不同的地方在于被索引数组的相关值会替代索引数组对应位置的值。如下索引数组的形状是2*2,返回的结果也是2*2的数组;由于被索引数组在1、2、3、4位置上的值正好也是1、2、3、4,所以返回的结果和索引数组一模一样,如下图所示:

假设现在有一个4*4的二维数组,需要选出其对角线上的元素,如下图所示。首先选出各行,行号包括[0,1,2,3];然后从各行里选择相应的对角线上元素的列号,也正好是[0,1,2,3]。

可以通过在索引数组内重新排列各行的行号来定义索引的顺序,如下图。也可以使用负值来索引数组,如下图。

9.4.2 布尔索引
布尔索引是另一种高级索引方式。当索引的是布尔数组的时候,就会触发布尔索引。首先使用random下的rand()函数生成一个10*4的均匀分布的二维数组;然后定义一个长度为10的一维数组,数组元素是一些人名,每行数据和人名一一对应,如图所示:

假设要筛选出所有与‘小王’相关的数据,如图所示:

name == ‘小王’
会生成一个布尔数组,凡是name这个数组里元素值是‘小王’的,布尔值是True;其余的则为False,如图所示:

在布尔索引的同时也可以进行分片操作,如下图所示:

还可以和之前介绍 的整数索引结合起来使用,如下图所示:

可以使用!=(不等于)筛选出除‘小王’以外的其他数据,如下图所示:

还可以使用逻辑运算符&(与)、|(或)、~(非)连接多个逻辑表达式,进行更加复杂的布尔索引操作。比如,上面使用!=比较运算符筛选出了不属于‘小王’的数据,也可以使用逻辑运算符得到相同的结果。如下图所示:

要筛选出属于‘小王’或者‘小张’的数据,如下图:

9.4.3 布尔索引的简单应用
在进行数据分析的时候,经常会剔除数据集内的默认值。定义一个带有nan(在Numpy中代表‘无’的意思)的二维数组,并使用isnan()函数筛选出为nan的数组元素,并且剔除它们,如下图:

还可以对数组内的某些特殊元素进行修改。比如,给数组内元素值小于1的元素加上一个值,如下图:

nonzero()函数可以用来生成数组元素值非0的整数数组索引,如下图:

布尔索引数组必须和被索引数组对应轴上的长度一样,否则会引发异常。因为布尔索引数组只有True和False两个值,如果和索引数组对应轴上的长度不一样,那么Numpy不知道要对哪个位置上的元素进行操作。
9.5 改变数组的形状
数组的形状可以被改变,使得元素重新排列,但是并不改变元素本身。比如之前使用的reshape()函数,如图所示,输入参数是表示数组形状的序列。
在reshape()函数的操作中,如果某个方向上的大小设为-1,则会自动根据其他方向上设定的大小来计算-1这个方向上的大小,如图所示。

在线性代数中,经常会对矩阵进行转置。数组也有一个特殊的T属性,可以执行类似矩阵的转置操作,如图所示。对于纬度大于2的数组,可以使用transpose()函数来进行重新排列。通过排列各个轴的轴号,从而实现数组结构的改变,如下图所示

还可以使用ravel()函数改变数组的形状,与reshape()函数不同的是,它将直接对原数组进行修改,如下图所示。

9.6 组装、分割数组
可以把位于不同方向上的几个数组组装起来。比如,有两个二维数组,可以在垂向上把它们组装起来,如下图:

也可以在横向上把两个树组组装起来,如下图:

反过来也可以对数组进行分割操作,比如,通过在第2列和第4列对数组进行分割,得到三个数组,三个数组在横轴上的长度分别为2/2/4,如下图

9.7 数组的基本函数
Numpy提供了一些基本函数,如exp()、sin()、add()等,可以非常方便地对数组内的元素进行运算,运算结果一般也是数组, 如下图所示:

还有一个比较常用的函数argmax(),用来返回某个轴上最大值的位置。如果没有定义轴的方向,则数组自动扩展成一维数组,然后返回最大元素的索引值,如下图所示:
在线性代数的运算中,经常需要进行矩阵乘法运算。Numpy提供了dot()函数,可以对两个形状匹配的二维数组进行矩阵乘法运算,如下图:

下表列出了一些常用的数组函数,包括数组的算术运算、三角函数、比较运算、浮点函数4类。


9.8 复制和指代
前面介绍了众多与数组相关的函数,有的函数是先对原数组进行复制再进行操作的,有的函数则是直接对原数组进行修改,然后返回一个对原数组的指代(view)。一般有三种情况:完全不复制、返回指代和深度复制。
1.完全不复制
赋值操作属于完全不复制数组的一类操作,如下图:

2.返回指代
不同的变量可以指向同一个数组。使用数组的view()方法可以生成一个数组对象,指代同一个数组,如下图。分片操作也可以返回一个对原数组的指代,如下图。

完全不复制和返回指代的共同点是都没有复制原数组。
3.深度复制
copy()方法会创建一个新的数组对象,而不是建立一个对原数组的索引。通俗来说,就是原数组和新的数组没有任何关系,任何对新数组的操作都不会影响到原数组,如下图:

9.9 线性代数
Numpy可用于计算矩阵相乘、分解矩阵、求解线性方程等线性代数问题。之前已经介绍过可以使用dot()函数求解矩阵相乘。使用MATLAB的用户需要注意,不能使用“*”运算符直接计算两个矩阵的乘积,因为该运算符在Numpy中用于两个数组相乘,如下图所示:

numpy.linalg模块中有矩阵计算经常会用到的功能,如inv()函数,用于求解矩阵的逆矩阵,如下图所示:

导入这个模块的方法如下:
import numpy.linalg as LA
可以使用solve()函数求解下面这个线性方程组,如下图所示:

使用eig()函数求解一个矩阵的特征值和特征向量,如下图所示

这里q是一个对角线上元素为4,5,6的对角矩阵。使用eig()函数求解该矩阵后,同时返回该矩阵的特征值和对应的特征向量。
9.10 使用数组来处理数据
在使用numpy数组处理数据的时候,可以避免重复地写循环语句;使用Numpy表达式可以节约大量的编程时间,把更多的精力投入到数据处理分析本身,而不需要关注繁琐的细节问题。
首先使用Numpy的mgrid()函数创建一个多维的网格。mgird()函数的输入参数是与所创建的网格相关的序列值,返回值是与网格坐标相关的两个数组,两个数组的组合代表了序列值可能生成的所有坐标对,如下图:
然后使用之前介绍的Numpy基本函数,根据x,y坐标计算Z值,如下图所示:
最后使用Matololib绘制Z=f(x,y)的关系,如下图



9.11 Numpy的where()函数和统计函数
筛选满足一定条件的数组元素是数据处理经常会遇到的任务。Numpy为了避免用户重复书写代码,提供了where()函数,使得用户可以非常简捷地筛选数据。数据的统计分析离不开求和、计算方差等基本函数,通过对这些基本函数的掌握,用户可以实现更加复杂的逻辑和应用。
9.11.1 where()函数
where()函数的语法是where(condition,[x,y])。使用这个函数可以方便地进行数组在一定条件下的筛选。比如,有三个数组a、b、c,其中c是bool数组。现在要在bool数组元素为Ture时,选择a数组对应位置的元素放到d数组中;否则,选择b数组对应位置的元素放在d数组中,如图所示:

常规的做法是使用for循环来筛选相应的元素,如下图:

可以看出这种方法还是比较麻烦的,可以使用where()函数非常简捷地得到同样的结果,如下图:

where()函数的第二个参数和第三个参数也可以不是数组,如下图:

这里的操作是:凡是数组a内大于0的值,设定为1;小于或者等于0的值,设定为0。
9.11.2 统计函数
统计函数是Numpy提供的用于数据分析的基础函数,在处理数据的时候经常会用到。sum()函数用于计算整个数组元素的和,或者在某一个轴向上元素的和,如下图:

mean()函数用于计算整个数组元素的平均值,或者某一个轴向上元素的平均值,如下图:

min()、max()函数分别用于返回数组元素的最小值、最大值,或者某一个轴向上元素的最小值和最大值,如下图:

std()、var()函数分别用于计算数组元素的标准差和方差,如下图:

argmin()、argmax()函数分别用于计算最小、最大元素的索引值,如下图:

cumsum()函数用于计算数组元素的累加和,比如,分别计算三列元素的累加和,如下图:

9.12 输入与输出
Numpy数组可以写入文件中,并保存下来,反过来,也可以从文件中读取数据,生成Numpy数组。常用的文件格式包括二进制文件和文本文件。
9.12.1 二进制文件
Numpy提供了load()、save()、savez()、savez_compressed()这4个函数来处理二进制文件。在使用Numpy的save()函数保存数组的时候,会生成一个扩展名为.npy的二进制文件,如下图所示:

使用load()函数导入保存的.npy文件,如下图:

也可以使用savez()函数将多个数组以非压缩的方式写入同一个二进制文件中,如下图:

如果不对写入文件的数组命名,那么Numpy会以array_0,array_1,...对其命名。同样可以使用load()函数读取文件内的数组,并以字典形式返回,如下图:

如果不知道数组的名字,则可以使用files属性查看文件内保存的所有数组名。使用savez_compressed()函数可以把多个数组以压缩的格式保存在二进制文件中。
9.12.2 文本文件
操作文本文件是数据处理经常遇到的任务,下面介绍一下处理文本文件的savetxt()和loadtxt()函数。和save()函数相比,savetxt()函数可以通过delimiter参数定义数组元素在文本文件中的分隔符号。比如,使用‘,’来分隔数组元素在文本文件中的保存方式,如下图所示:

使用文本编辑器打开out.txt文件,可以看到用逗号分隔的数字(CSV格式的文本)。

9.14 数组的排序和查找
9.14.1 排序
Numpy提供了sort()函数,它将复制数组并返回排序结果,如下图所示:

如果是多维数组,则可以设置axis参数定义需要排序的轴,sort()函数会对这个轴向上的所有元素排序,如下图所示:

sort()函数的order参数重新定义排序的关键字段。现有小明、小张、小王、小李4位同学的身高和体重数据,如下图:

先以‘身高’字段排序,如果身高一样,则以‘体重’字段对这几个人排序,排序结果如图所示:

数组对象也有一个sort()函数,与Numpy的上层的sort()函数的区别在于,ndarray.sort()函数是对数组进行原地排序,也就是直接修改原数组不会生成新的数组。
除sort()一类的直接排序函数外,Numpy还提供了间接排序函数,如lexsort()函数,用于返回排序结果的索引值,如下图所示:

这里使用lexsort()函数对a/b两个列表进行排序。lexsort()函数的输入参数可以是一个k*n的数组,也可以是k*n的有序数字,本例输入的是两个长度为5的列表,返回排序结果的索引值。读者可能会对这个排序方法感到迷惑,下面讲解一下为什么排序结果的第一个索引值为5。
该函数默认从最后一行开始向前依次进行排序。比如,本例首先对b列表进行排序,该行最小的数是4,索引值是3和5;然后根据a列表里的数字排序,索引位置3和5对应的数是2和1,所以索引位置5应该排在3的前面。
9.14.2 查找
seachsorted()是查找数组元素时经常用到的函数。查找一个合适的位置,将元素插入已排好序的一维数组中,并且保持数组元素的顺序不被打乱,如下图:

除了可以输入某个数外,还可以输入一个序列,如下图:

注意:这里返回的是一个数组,对应序列中数字的合适位置
seachsorted()函数还有一个side参数,在默认情况下,该参数的值是‘left’,假设数组有多个位置与查找的数字匹配,则会返回第一个位置;如果要将该参数设置为‘right’,则会返回最后一个位置,如下图:

extract()函数可以用来提取满足一定条件的元素,比如,提取0,1,...,16中不能被4整除的数,如下图:

引用说明
《Python数据分析从入门到精通》 张啸宇 李静 编著
往期文章
1. Python3的33个保留字详解-CSDN博客
2. Python3 学习起步必备知识点-CSDN博客
3. Python3 数据类型与流程控制语句-CSDN博客
4. Python3 可复用的函数与模块-CSDN博客
6. Python3 面向对象的Python-CSDN博客
7. Python3 异常处理与程序调试-CSDN博客
8. Python3 pandas数据分析处理库-CSDN博客