目录

摘要

ABSTRACT

一、文献阅读

一、题目

二、摘要

三、文献解读

一、Introduction

二、KINN框架

三、主要结果

四、Conclusion

二、KAN

一、KAN与MLP区别

二、KAN网络解析

三、激活函数参数化（B-splines）

三、网络架构代码

摘要

本周我阅读了一篇题目为Kolmogorov–Arnold-Informed neural network: A physics-informed deep learning framework for solving PDEs based on Kolmogorov–Arnold Networks的文献，它是将PINN中的网络架构用KAN来代替，提出了KINN。其次对KAN和KAN的网络架构进行了初步学习，加深了对其的认识。

ABSTRACT

This week I read a paper titled "Kolmogorov–Arnold-Informed Neural Network: A Physics-Informed Deep Learning Framework for Solving PDEs Based on Kolmogorov–Arnold Networks." The paper proposes replacing the network architecture in PINN with KAN, introducing KINN. Additionally, I conducted a preliminary study of KAN and its network architecture, which deepened my understanding of it.

一、文献阅读

一、题目

题目：Kolmogorov–Arnold-Informed neural network: A physics-informed deep learning framework for solving PDEs based on Kolmogorov–Arnold Networks

链接：https://arxiv.org/html/2406.11045v1

二、摘要

受Kolmogorov-Arnold表示定理的启发，本文提出Kolmogorov-Arnold网络(KAN)作为多层感知器(MLP)的有前途的替代品。MLP在节点(“神经元”)上有固定的激活函数，而KAN在边缘(“权重”)上有可学习的激活函数。KAN根本没有线性权重——每个权重参数都被参数化为样条的单变量函数所取代。这个看似简单的改变使得KAN在准确性和可解释性方面优于MLP。就准确性而言，在数据拟合和PDE求解方面，更小的KAN可以达到与更大的MLP相当或更好的准确性。从理论和经验上看，KAN比MLP具有更快的神经尺度规律。对于可解释性，KAN可以直观地可视化，并且可以轻松地与人类用户交互。通过数学和物理的两个例子，KAN被证明是有用的“合作者”，帮助科学家(重新)发现数学和物理定律。

Inspired by the Kolmogorov-Arnold representation theorem, this paper proposes the Kolmogorov-Arnold Network (KAN) as a promising alternative to the Multilayer Perceptron (MLP). While MLPs have fixed activation functions at the nodes ("neurons"), KANs feature learnable activation functions at the edges ("weights"). KANs have no linear weights at all—each weight parameter is replaced by a univariate function parameterized as a spline. This seemingly simple change enables KANs to surpass MLPs in terms of both accuracy and interpretability. In terms of accuracy, smaller KANs can achieve comparable or better accuracy than larger MLPs in data fitting and PDE solving. Both theoretically and empirically, KANs exhibit faster neural scaling laws than MLPs. For interpretability, KANs can be intuitively visualized and can easily interact with human users. Through two examples from mathematics and physics, KANs are demonstrated to be useful "collaborators" in helping scientists (re)discover mathematical and physical laws.

三、文献解读

一、Introduction

用于PDEs的AI中有三种重要的方法：物理信息神经网络（PINNs）、算子学习和物理信息神经算子（PINO）。PINNs：由于同一个PDE可以有不同的表达形式，每种形式的准确性和效率各不相同，基于这些表达形式开发了不同形式的PINNs。这些形式包括强形式的PINNs、弱形式的PINNs（hp-VPINNs）、能量形式的PINNs（深度能量方法：DEM）和逆形式的PINNs（边界元方法：BINN）。算子学习：代表性的有DeepONet和傅里叶神经算子（FNO）。最初提出的算子学习方法完全是数据驱动的，非常适合大数据问题。PINO：它将物理方程与算子学习结合起来。通过在算子学习的训练过程中加入物理方程，传统的算子学习可以实现更高的精度。此外，PINO可以利用算子学习首先获得一个好的近似解，然后使用PDEs进行精细化，大大加快了PDEs的计算速度。KAN（Kolmogorov-Arnold网络）加深了浅层Kolmogorov网络，创造了具有良好性质的单变量函数。KAN与MLP非常相似，主要区别在于KAN的激活函数需要学习。在原始的KAN中，由于其出色的拟合能力，使用B样条作为激活函数的构建。KAN的核心是引入了一个可以学习激活函数的复合函数框架。因此本文提出了KINN，它是PDEs不同形式（强形式、能量形式和逆形式）的KAN版本。由于在使用不同逼近函数替代B样条的广泛工作，我们使用原始的B样条版本的KAN与PDEs的不同形式的MLP直接比较，系统地比较精度和效率是否有所改善。KAN的参数比MLP少，而且由于KAN的激活函数是B样条，KAN的函数构建更符合解决PDEs的数值算法的本质。因此，有理由相信将KAN与各种形式的PINNs结合以替代MLP将取得更好的结果。

二、KINN框架

KINN的思想是在不同形式的PDEs（强形式、能量形式和逆形式）中用Kolmogorov-Arnold网络（KAN）替代MLP。在KAN中，主要训练参数是激活函数中B样条的未确定系数。KINN基于PDEs的不同数值格式建立损失函数并优化。虚拟网格的大小由KAN中的网格尺寸决定。

三、主要结果

验证MLP和KAN在拟合时的“频谱偏差”。(a) 精确解、MLP预测和KAN预测在训练周期100, 1000和10000时的情况；(b) MLP和KAN的特征值分布；(c) 第一行是从大到小排序的最大特征值的特征向量，第二行是最小三个特征值的特征向量；(d) MLP和KAN的损失函数的演变。

MLP和KAN拟合高低频混合热传导问题。(a) 频率为 (F = 50) 的精确解；(b) 在5000次迭代后，频率 (F = 50) 的MLP预测；(c) 在5000次迭代后，频率 (F = 50) 的MLP的绝对误差；(d) 在5000次迭代后，频率 (F = 50) 的KAN预测；(e) 在5000次迭代后，频率 (F = 50) 的KAN的绝对误差；(f) 在不同网格尺寸和频率下，经过3000次迭代及网络结构为[2,5,1]的KAN的相对误差。

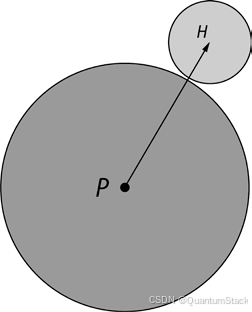
介绍模式III裂纹。(a) 模式III裂纹的结构，位于一个正方形区域内，尺寸为。蓝色和黄色区域代表两个神经网络，因为裂纹处的位移是不连续的（x<0,y=0），因此需要两个神经网络来拟合裂纹上下的位移。(b) 这个问题的解析解为 ，其中r是从坐标x到原点x=y=0的距离， 是角度，以x>0,y=0为参考，逆时针方向为正角。(c) KINN的网格分布，顺序为3，网格大小为10，在x和y方向上均匀分布。(d) 用于PINN、DEM和KINN的无网格随机采样点。红色点代表上部区域神经网络的必要边界位移点（256点），蓝色点代表下部区域神经网络的点（2048点），黄色点是接口采样点（1000点）。

不同的基于MLP或KAN的PINNs、DEM和BINN算法之间的比较。参数意味着NNs架构中的训练参数。相对误差代表收敛时的L2误差。网格范围是KAN网格的初始范围。阶数是KAN中B样条的阶数。NNs的架构是相应神经网络的结构。参数是相应网络的可训练参数。时间是相应算法1000个周期的持续时间。

PINNs、DEM、BINN及其对应的KINN版本预测的位移解：(a) FEM参考解，(b) PINNs，(c) DEM，(d) BINN，(e) KINN-PINNs，(f) KINN-DEM，(g) KINN-BINN。

四、Conclusion

本文比较了KAN和MLP在不同形式的偏微分方程（PDE）中的表现，并提出了KINN算法用于解决KAN在强形式、能量形式和逆问题中的PDE。进行了系统的数值实验和工程力学常见基准验证。结果显示，在大多数PDE问题中，特别是在奇异性问题、应力集中问题、非线性超弹性问题和异质问题中，KAN具有比MLP更高的精度和收敛速度。然而，由于KAN算法缺乏特定的优化，其效率目前比同样epoch下的MLP低。通过优化，KINN的效率可以显著提高。此外，从NTK（神经正切核）的角度系统分析了KAN，发现其谱偏差远小于MLP，使其更适合解决高低频混合问题。最后，我们发现KAN在复杂几何PDE问题上表现不佳，主要是由于网格尺寸与几何复杂性之间的冲突。然而，目前KINN存在局限性和扩展空间。在实验过程中，我们发现过大的网格尺寸可能导致KAN失败，即由于过拟合而增加误差。因此，在使用KINN时，根据问题的复杂性确定合适的网格尺寸至关重要。

二、KAN

一、KAN与MLP区别

MLP：线性组合，非线性激活
KAN：非线性激活（每个输入），线性组合

可以理解为顺序换了一下，下图左边是MLP，右边是KAN，很好理解。最大的点是激活函数不再是固定的Sigmoid或ReLU，它被参数化了，可学。

二、KAN网络解析

就是f是一个多元函数（有多个x变量，吐出来一个数），可以被表示为多个单元函数的线性组合，就是单元函数和加法，可以构建出乘法！

其实两层理论上可以拟合任何函数，但是激活函数有时会变得非常不光滑，非常病态，才能满足要求，所以这也是多层KAN的必要性。

三、激活函数参数化（B-splines）

激活函数所以必须先参数化，才能 learnable。作者是选了B样条函数下图说明了这个样条函数怎么来的：

其实就是多个basic函数的相加，C参数控制每个basic的幅值。Φ函数有粗粒度和细粒度选择，就是选多些basic函数相加就越精准嘛，上图是展示7和12两种情况。G=5表示interval是5。

MLPs通过增加模型的宽度和深度可以提高性能，但这种方法效率低下，因为需要独立地训练不同大小的模型。KANS:开始可以用较少的参数训练，然后通过简单地细化其样条网格来增加参数，无需重新训练整个模型。基本原理就是通过将样条函数(splines)旧的粗网格转换为更细的网格，并对应地调整参数，无需从头开始训练就能扩展现有的 KAN 模型。这种技术称为“网格扩展”(grid extension)。

三、网络架构代码

class KANLinear(torch.nn.Module):
    def __init__(
        self,
        in_features,
        out_features,
        grid_size=5,
        spline_order=3,
        scale_noise=0.1,
        scale_base=1.0,
        scale_spline=1.0,
        enable_standalone_scale_spline=True,
        base_activation=torch.nn.SiLU,
        grid_eps=0.02,
        grid_range=[-1, 1],
    ):
        super(KANLinear, self).__init__()
        self.in_features = in_features
        self.out_features = out_features
        self.grid_size = grid_size
        self.spline_order = spline_order

        h = (grid_range[1] - grid_range[0]) / grid_size
        grid = (
            (
                torch.arange(-spline_order, grid_size + spline_order + 1) * h
                + grid_range[0]
            )
            .expand(in_features, -1)
            .contiguous()
        )
        self.register_buffer("grid", grid)

        self.base_weight = torch.nn.Parameter(torch.Tensor(out_features, in_features))
        self.spline_weight = torch.nn.Parameter(
            torch.Tensor(out_features, in_features, grid_size + spline_order)
        )
        if enable_standalone_scale_spline:
            self.spline_scaler = torch.nn.Parameter(
                torch.Tensor(out_features, in_features)
            )

        self.scale_noise = scale_noise
        self.scale_base = scale_base
        self.scale_spline = scale_spline
        self.enable_standalone_scale_spline = enable_standalone_scale_spline
        self.base_activation = base_activation()
        self.grid_eps = grid_eps

        self.reset_parameters()

    def reset_parameters(self):
        torch.nn.init.kaiming_uniform_(self.base_weight, a=math.sqrt(5) * self.scale_base)
        with torch.no_grad():
            noise = (
                (
                    torch.rand(self.grid_size + 1, self.in_features, self.out_features)
                    - 1 / 2
                )
                * self.scale_noise
                / self.grid_size
            )
            self.spline_weight.data.copy_(
                (self.scale_spline if not self.enable_standalone_scale_spline else 1.0)
                * self.curve2coeff(
                    self.grid.T[self.spline_order : -self.spline_order],
                    noise,
                )
            )
            if self.enable_standalone_scale_spline:
                # torch.nn.init.constant_(self.spline_scaler, self.scale_spline)
                torch.nn.init.kaiming_uniform_(self.spline_scaler, a=math.sqrt(5) * self.scale_spline)

    def b_splines(self, x: torch.Tensor):
        """
        Compute the B-spline bases for the given input tensor.

        Args:
            x (torch.Tensor): Input tensor of shape (batch_size, in_features).

        Returns:
            torch.Tensor: B-spline bases tensor of shape (batch_size, in_features, grid_size + spline_order).
        """
        assert x.dim() == 2 and x.size(1) == self.in_features

        grid: torch.Tensor = (
            self.grid
        )  # (in_features, grid_size + 2 * spline_order + 1)
        x = x.unsqueeze(-1)
        bases = ((x >= grid[:, :-1]) & (x < grid[:, 1:])).to(x.dtype)
        for k in range(1, self.spline_order + 1):
            bases = (
                (x - grid[:, : -(k + 1)])
                / (grid[:, k:-1] - grid[:, : -(k + 1)])
                * bases[:, :, :-1]
            ) + (
                (grid[:, k + 1 :] - x)
                / (grid[:, k + 1 :] - grid[:, 1:(-k)])
                * bases[:, :, 1:]
            )

        assert bases.size() == (
            x.size(0),
            self.in_features,
            self.grid_size + self.spline_order,
        )
        return bases.contiguous()

    def curve2coeff(self, x: torch.Tensor, y: torch.Tensor):
        """
        Compute the coefficients of the curve that interpolates the given points.

        Args:
            x (torch.Tensor): Input tensor of shape (batch_size, in_features).
            y (torch.Tensor): Output tensor of shape (batch_size, in_features, out_features).

        Returns:
            torch.Tensor: Coefficients tensor of shape (out_features, in_features, grid_size + spline_order).
        """
        assert x.dim() == 2 and x.size(1) == self.in_features
        assert y.size() == (x.size(0), self.in_features, self.out_features)

        A = self.b_splines(x).transpose(
            0, 1
        )  # (in_features, batch_size, grid_size + spline_order)
        B = y.transpose(0, 1)  # (in_features, batch_size, out_features)
        solution = torch.linalg.lstsq(
            A, B
        ).solution  # (in_features, grid_size + spline_order, out_features)
        result = solution.permute(
            2, 0, 1
        )  # (out_features, in_features, grid_size + spline_order)

        assert result.size() == (
            self.out_features,
            self.in_features,
            self.grid_size + self.spline_order,
        )
        return result.contiguous()

    @property
    def scaled_spline_weight(self):
        return self.spline_weight * (
            self.spline_scaler.unsqueeze(-1)
            if self.enable_standalone_scale_spline
            else 1.0
        )

    def forward(self, x: torch.Tensor):
        assert x.size(-1) == self.in_features
        original_shape = x.shape
        x = x.reshape(-1, self.in_features)

        base_output = F.linear(self.base_activation(x), self.base_weight)
        spline_output = F.linear(
            self.b_splines(x).view(x.size(0), -1),
            self.scaled_spline_weight.view(self.out_features, -1),
        )
        output = base_output + spline_output
        
        output = output.reshape(*original_shape[:-1], self.out_features)
        return output

    @torch.no_grad()
    def update_grid(self, x: torch.Tensor, margin=0.01):
        assert x.dim() == 2 and x.size(1) == self.in_features
        batch = x.size(0)

        splines = self.b_splines(x)  # (batch, in, coeff)
        splines = splines.permute(1, 0, 2)  # (in, batch, coeff)
        orig_coeff = self.scaled_spline_weight  # (out, in, coeff)
        orig_coeff = orig_coeff.permute(1, 2, 0)  # (in, coeff, out)
        unreduced_spline_output = torch.bmm(splines, orig_coeff)  # (in, batch, out)
        unreduced_spline_output = unreduced_spline_output.permute(
            1, 0, 2
        )  # (batch, in, out)

        # sort each channel individually to collect data distribution
        x_sorted = torch.sort(x, dim=0)[0]
        grid_adaptive = x_sorted[
            torch.linspace(
                0, batch - 1, self.grid_size + 1, dtype=torch.int64, device=x.device
            )
        ]

        uniform_step = (x_sorted[-1] - x_sorted[0] + 2 * margin) / self.grid_size
        grid_uniform = (
            torch.arange(
                self.grid_size + 1, dtype=torch.float32, device=x.device
            ).unsqueeze(1)
            * uniform_step
            + x_sorted[0]
            - margin
        )

        grid = self.grid_eps * grid_uniform + (1 - self.grid_eps) * grid_adaptive
        grid = torch.concatenate(
            [
                grid[:1]
                - uniform_step
                * torch.arange(self.spline_order, 0, -1, device=x.device).unsqueeze(1),
                grid,
                grid[-1:]
                + uniform_step
                * torch.arange(1, self.spline_order + 1, device=x.device).unsqueeze(1),
            ],
            dim=0,
        )

        self.grid.copy_(grid.T)
        self.spline_weight.data.copy_(self.curve2coeff(x, unreduced_spline_output))

    def regularization_loss(self, regularize_activation=1.0, regularize_entropy=1.0):
        """
        Compute the regularization loss.

        This is a dumb simulation of the original L1 regularization as stated in the
        paper, since the original one requires computing absolutes and entropy from the
        expanded (batch, in_features, out_features) intermediate tensor, which is hidden
        behind the F.linear function if we want an memory efficient implementation.

        The L1 regularization is now computed as mean absolute value of the spline
        weights. The authors implementation also includes this term in addition to the
        sample-based regularization.
        """
        l1_fake = self.spline_weight.abs().mean(-1)
        regularization_loss_activation = l1_fake.sum()
        p = l1_fake / regularization_loss_activation
        regularization_loss_entropy = -torch.sum(p * p.log())
        return (
            regularize_activation * regularization_loss_activation
            + regularize_entropy * regularization_loss_entropy
        )


class KAN(torch.nn.Module):
    def __init__(
        self,
        layers_hidden,
        grid_size=5,
        spline_order=3,
        scale_noise=0.1,
        scale_base=1.0,
        scale_spline=1.0,
        base_activation=torch.nn.SiLU,
        grid_eps=0.02,
        grid_range=[-1, 1],
    ):
        super(KAN, self).__init__()
        self.grid_size = grid_size
        self.spline_order = spline_order

        self.layers = torch.nn.ModuleList()
        for in_features, out_features in zip(layers_hidden, layers_hidden[1:]):
            self.layers.append(
                KANLinear(
                    in_features,
                    out_features,
                    grid_size=grid_size,
                    spline_order=spline_order,
                    scale_noise=scale_noise,
                    scale_base=scale_base,
                    scale_spline=scale_spline,
                    base_activation=base_activation,
                    grid_eps=grid_eps,
                    grid_range=grid_range,
                )
            )

    def forward(self, x: torch.Tensor, update_grid=False):
        for layer in self.layers:
            if update_grid:
                layer.update_grid(x)
            x = layer(x)
        return x

    def regularization_loss(self, regularize_activation=1.0, regularize_entropy=1.0):
        return sum(
            layer.regularization_loss(regularize_activation, regularize_entropy)
            for layer in self.layers
        )