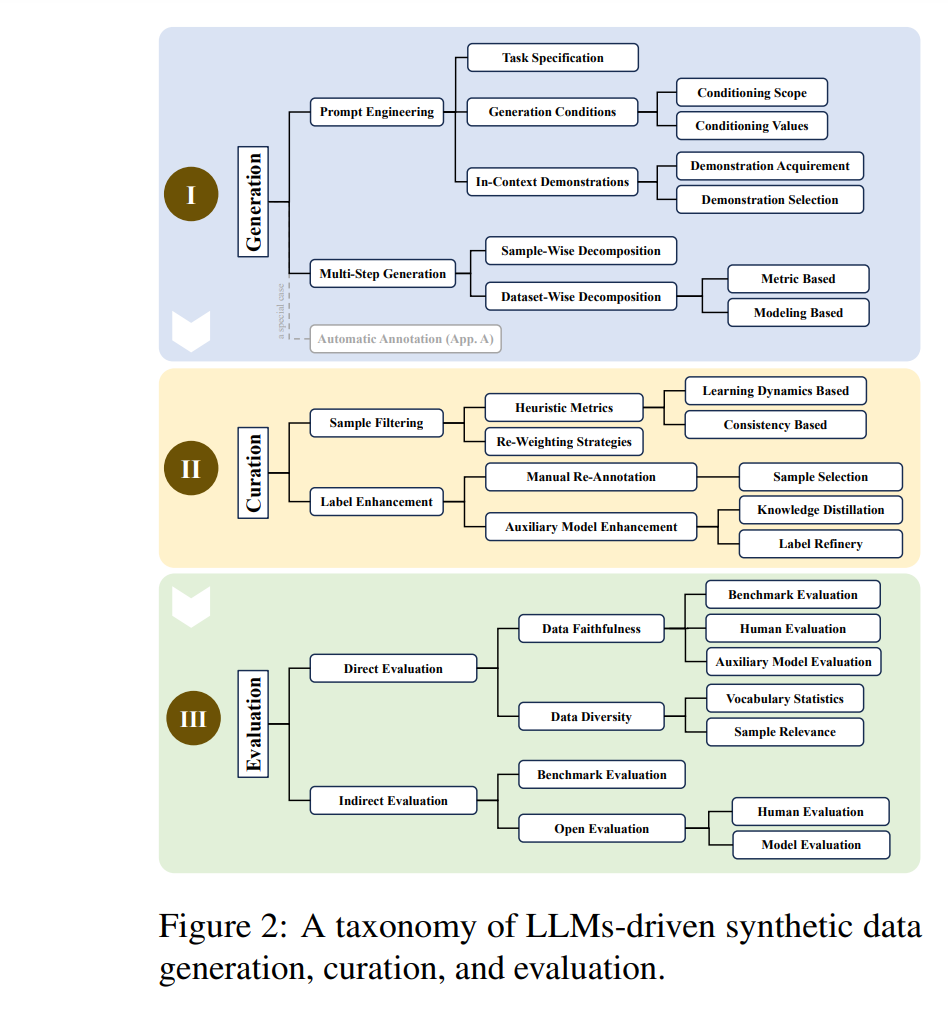
神经网络基本概念：

1. 神经元（Neuron）：

   神经网络的基本单元，接收输入，应用权重并通过激活函数生成输出。

2. 层（Layer）：

   神经网络由多层神经元组成。常见的层包括输入层、隐藏层和输出层。

3. 权重（Weights）和偏置（Biases）：

   权重用于调整输入的重要性，偏置用于调整模型的输出。

4. 激活函数（Activation Function）：

   在神经元中引入非线性，如ReLU（Rectified Linear Unit）、Sigmoid、Tanh等。

5. 损失函数（Loss Function）：

   用于衡量模型预测与实际结果之间的差异，如均方误差（MSE）、交叉熵损失等。

6. 优化器（Optimizer）：

   用于调整模型权重以最小化损失函数，如随机梯度下降（SGD）、Adam等。

简单的神经网络示例：

下面是一个使用PyTorch构建简单线性回归的神经网络示例代码。这个示例展示了如何定义一个具有一个隐藏层的前馈神经网络，并训练它来逼近一些随机生成的数据点。

import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt

# 生成一些随机数据
np.random.seed(0)
X = np.linspace(0, 10, 100).reshape(-1, 1).astype(np.float32)
y = np.sin(X) + np.random.normal(0, 0.1, size=X.shape).astype(np.float32)

# 转换为PyTorch的张量
X_tensor = torch.tensor(X)
y_tensor = torch.tensor(y)

# 定义一个简单的神经网络模型
class NeuralNet(nn.Module):
    def __init__(self):
        super(NeuralNet, self).__init__()
        self.fc1 = nn.Linear(1, 10)  # 输入层到隐藏层
        self.relu = nn.ReLU()        # 激活函数
        self.fc2 = nn.Linear(10, 1)  # 隐藏层到输出层

    def forward(self, x):
        x = self.fc1(x)
        x = self.relu(x)
        x = self.fc2(x)
        return x

# 实例化模型、损失函数和优化器
model = NeuralNet()
criterion = nn.MSELoss()  # 均方误差损失函数
optimizer = optim.Adam(model.parameters(), lr=0.01)  # Adam优化器

# 训练模型
epochs = 5000
losses = []
for epoch in range(epochs):
    optimizer.zero_grad()
    outputs = model(X_tensor)
    loss = criterion(outputs, y_tensor)
    loss.backward()
    optimizer.step()
    
    losses.append(loss.item())
    if (epoch+1) % 1000 == 0:
        print(f'Epoch [{epoch+1}/{epochs}], Loss: {loss.item():.6f}')

# 绘制损失函数变化图
plt.plot(losses, label='Training loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()

# 测试模型
model.eval()
with torch.no_grad():
    test_x = torch.tensor([[5.0]])  # 测试输入
    predicted = model(test_x)
    print(f'预测值: {predicted.item()}')

运行结果展示: 

代码理解：

下面便是详细分解这段代码进行理解： 

• 生成数据：

  • 使用 numpy 生成一些随机的带有噪声的正弦函数数据。

    import numpy as np
    
    # 生成带有正态分布噪声的正弦函数数据
    def generate_data(n_samples):
        np.random.seed(0)  # 设置随机种子以确保结果可复现
        X = np.random.uniform(low=0, high=10, size=n_samples)
        y = np.sin(X) + np.random.normal(scale=0.3, size=n_samples)
        return X, y
    
    # 生成数据
    X_train, y_train = generate_data(100)
    

• 定义神经网络模型：

  • NeuralNet 类继承自 nn.Module，定义了一个具有一个隐藏层的前馈神经网络。使用ReLU作为隐藏层的激活函数。

    import torch
    import torch.nn as nn
    import torch.optim as optim
    
    # 定义神经网络模型
    class NeuralNet(nn.Module):
        def __init__(self):
            super(NeuralNet, self).__init__()
            self.fc1 = nn.Linear(1, 10)  # 输入大小为1（X），输出大小为10
            self.fc2 = nn.Linear(10, 1)  # 输入大小为10，输出大小为1
            self.relu = nn.ReLU()
    
        def forward(self, x):
            x = self.relu(self.fc1(x))
            x = self.fc2(x)
            return x
    
    # 实例化模型
    model = NeuralNet()
    
    # 打印模型结构
    print(model)
    

• 实例化模型、损失函数和优化器：

  • model 是我们定义的神经网络模型。
  • criterion 是损失函数，这里使用均方误差损失。
  • optimizer 是优化器，这里使用Adam优化器来更新模型参数。

    # 定义损失函数（均方误差损失）
    criterion = nn.MSELoss()
    
    # 定义优化器（Adam优化器）
    optimizer = optim.Adam(model.parameters(), lr=0.01)
    

• 训练模型：

  • 使用 X_tensor 和 y_tensor 进行训练，优化模型使其逼近 y_tensor。

    # 将numpy数组转换为PyTorch张量
    X_tensor = torch.tensor(X_train, dtype=torch.float32).view(-1, 1)
    y_tensor = torch.tensor(y_train, dtype=torch.float32).view(-1, 1)
    
    # 训练模型
    def train_model(model, criterion, optimizer, X, y, epochs=1000):
        model.train()
        for epoch in range(epochs):
            optimizer.zero_grad()
            output = model(X)
            loss = criterion(output, y)
            loss.backward()
            optimizer.step()
            if (epoch+1) % 100 == 0:
                print(f'Epoch [{epoch+1}/{epochs}], Loss: {loss.item():.4f}')
    
    train_model(model, criterion, optimizer, X_tensor, y_tensor)
    

• 测试模型：

  • 使用 model.eval() 将模型切换到评估模式，使用 torch.no_grad() 关闭梯度计算。
  • 测试输入为 5.0，打印预测结果。

    # 测试模型
    model.eval()
    with torch.no_grad():
        test_input = torch.tensor([[5.0]], dtype=torch.float32)
        predicted_output = model(test_input)
        print(f'预测输入为 5.0 时的输出: {predicted_output.item():.4f}')