关于全变分模型,可以参考:
如何理解全变分(Total Variation,TV)模型?- imxtx的回答 - 知乎
https://www.zhihu.com/question/47162419/answer/2585330101
全变分去噪的基本思想是,如果图像的细节有很多高频信息(如尖刺、噪点等),那么整幅图像的梯度幅值之和(全变分)是比较大的,如果能够使整幅图像的梯度积分之和降低,就达到了去噪的目的。
放在一维信号上,如下:

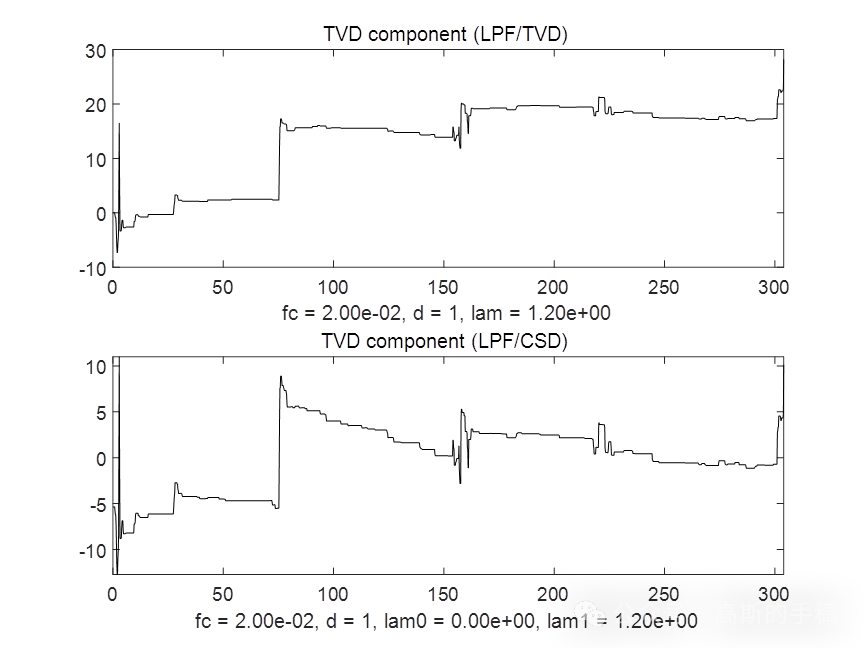
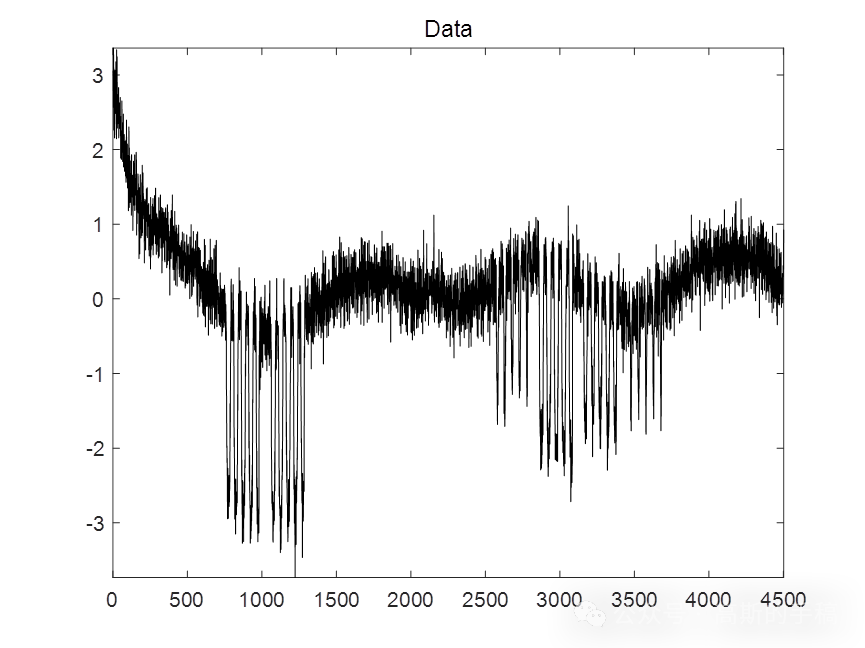
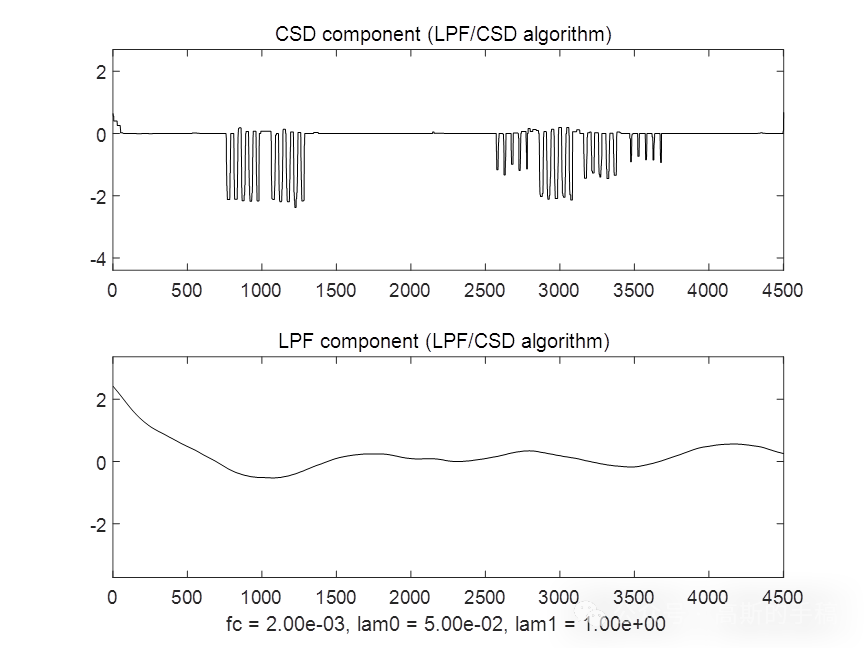
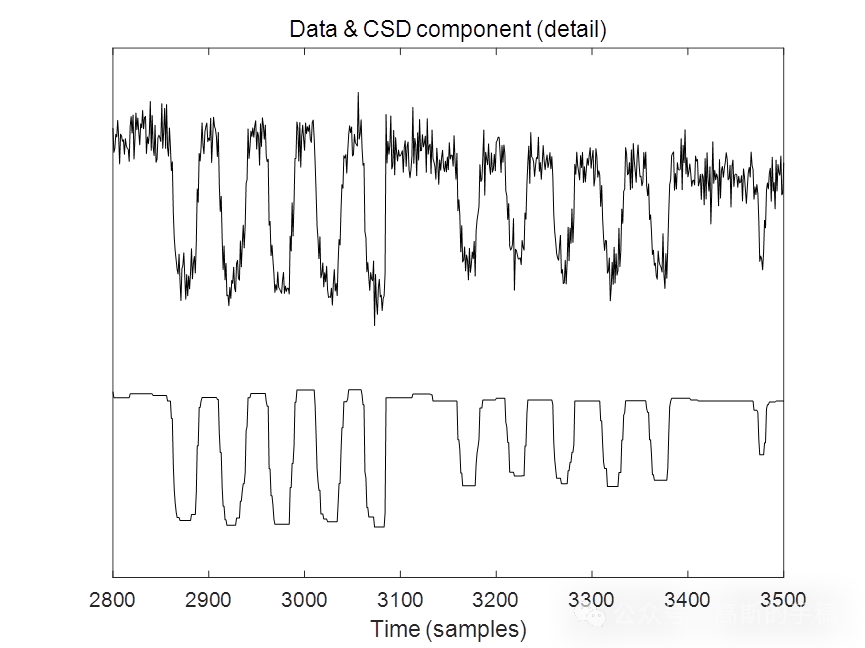
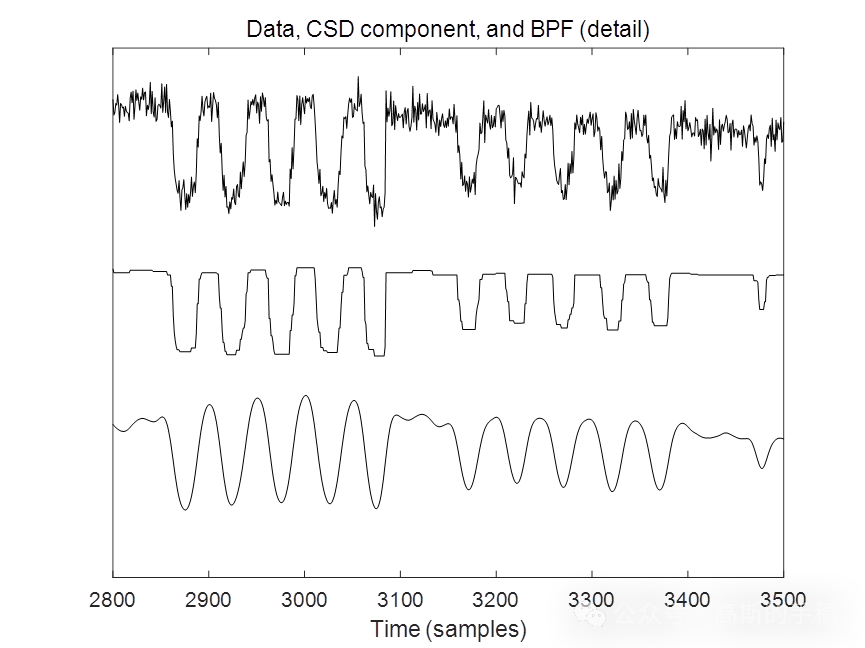
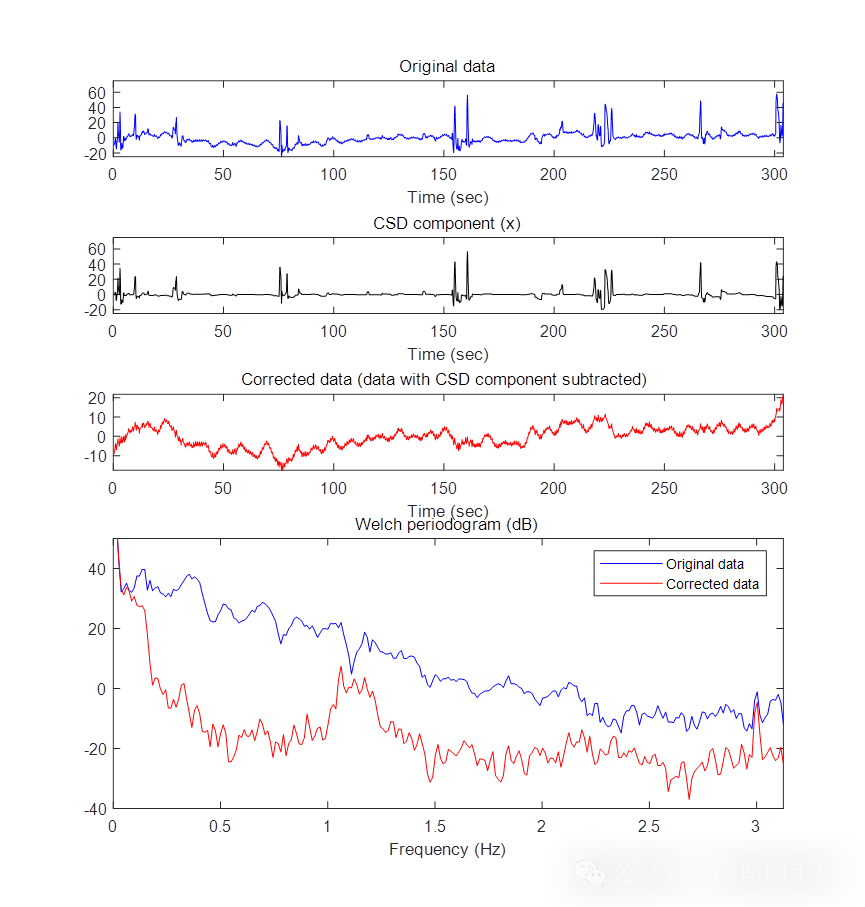
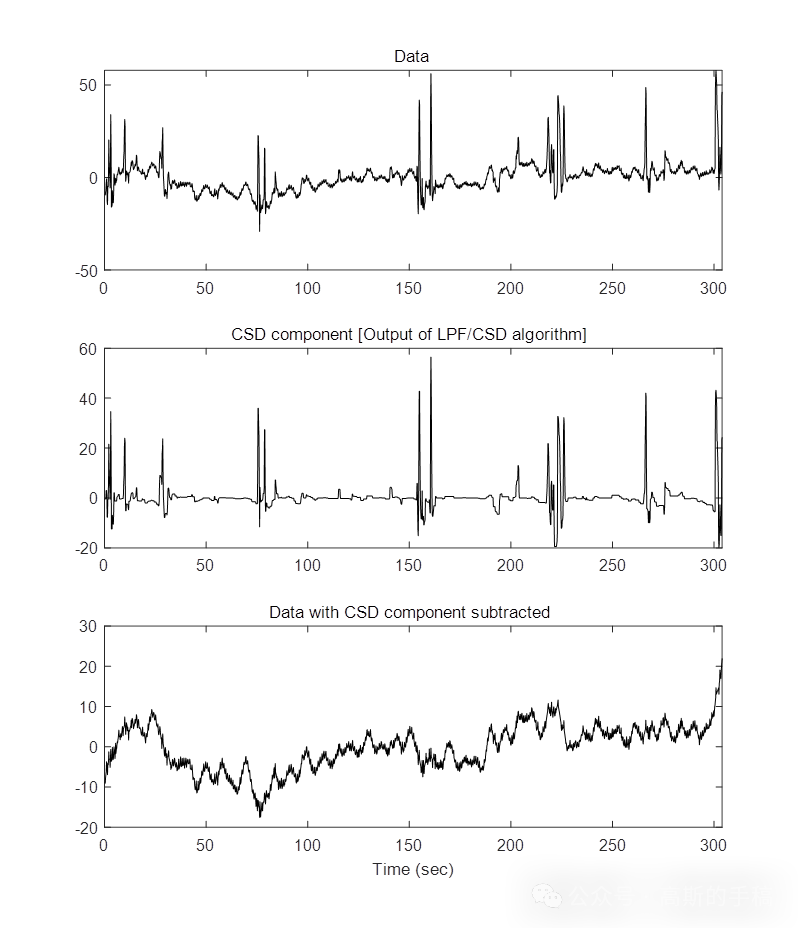
鉴于此,采用同步低通滤波结合全变分方法对一维时间序列进行降噪,运行环境为MATLAB 2018A。
function [A, B, B1, D, a, b, b1] = ABfilt(deg, fc, N)
% [A, B, B1] = ABfilt(d, fc, N)
%
% Banded matrices for zero-phase high-pass recursive filter.
% The matrices are created as 'sparse' structures.
%
% INPUT
% d : degree of filter is 2d
% fc : cut-off frequency (normalized frequency, 0 < fc < 0.5)
% N : length of signal
%
% OUTPUT
% A, B, B1 : banded filter matrices
% with B = B1*D where D is the first-order difference matrix
%
% Use [A, B, B1, D, a, b, b1] = ABfilt(...) to return
% filter coefficient vectors a, b, b1.
b1 = 1;
for i = 1:2*deg-1
b1 = conv(b1, [-1 1]);
end
b1 = b1 * (-1)^deg;
b = conv(b1, [-1 1]);
omc = 2*pi*fc;
t = ((1-cos(omc))/(1+cos(omc)))^deg;
a = 1;
for i = 1:deg
a = conv(a, [1 2 1]);
end
a = b + t*a;
A = spdiags( a(ones(N-2*deg,1), :), -deg:deg, N-2*deg, N-2*deg); % A: Symmetric banded matrix
B1 = spdiags(b1(ones(N,1), :), 0:2*deg-1, N-2*deg, N-1); % B1: banded matrix
e = ones(N, 1);
D = spdiags([-e e] , 0:1, N-1, N);
B = B1 * D; % B: banded matrix
% verify that B = B1*D
x = rand(N,1);
err = B1*diff(x) - B*x;
if max(abs(err)) > 1e-10
disp('Error in ABfilt (B1*D not equal to B)')
end
擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。
知乎学术咨询:https://www.zhihu.com/consult/people/792359672131756032?isMe=1
擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。
擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。