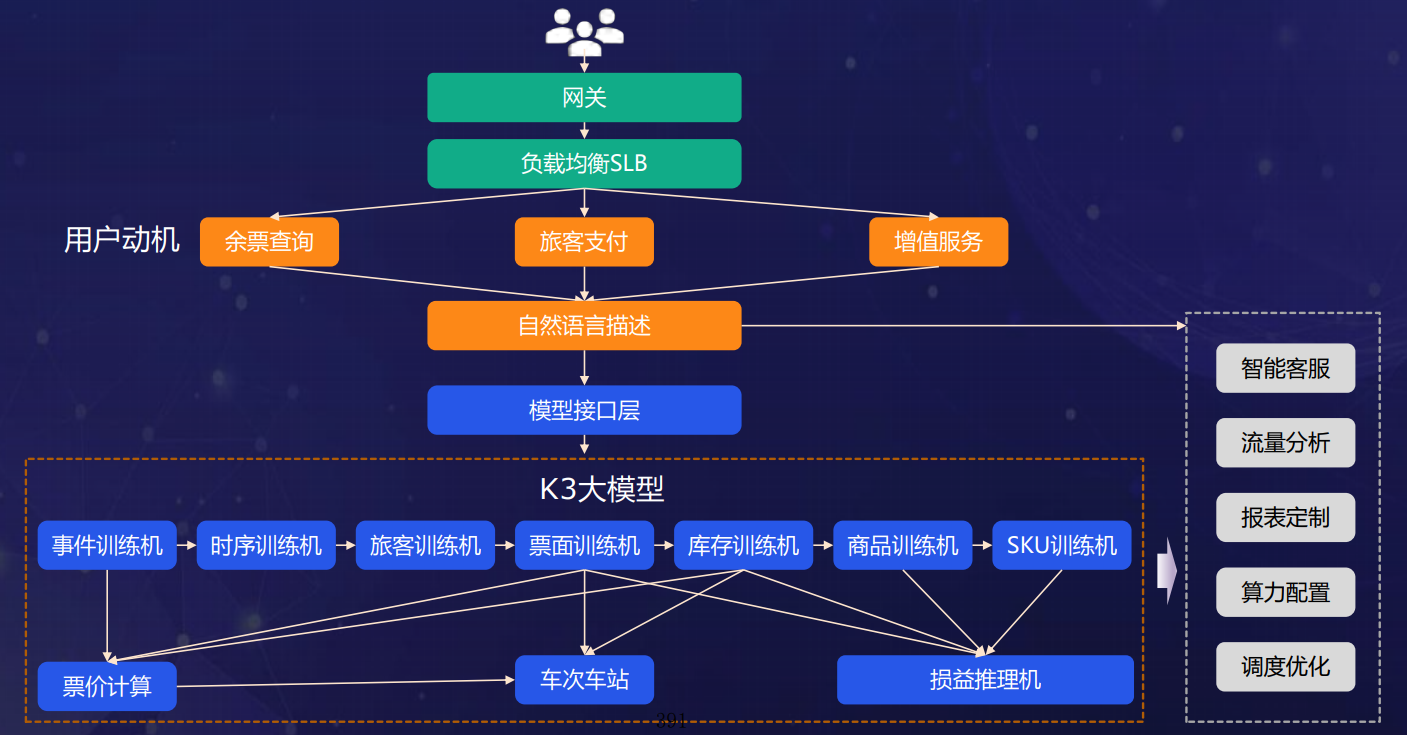
基于振动分析的故障诊断方法基本流程主要由以下五个步骤组成,分别是信号采集、信号处理、特征提取、状态识别与诊断结果。这五个步骤中信号采集与特征提取是故障诊断中最为重要的步骤,而故障微弱特征信息又是其中最难解决的问题。“故障微弱特征信息”站在狭义的角度可以认为是振动信号的幅值很小,广义上说其实是相对于噪声更弱的目标信号。对于此类目标信号的检测从根本上来说是研究如何消除噪声分量,从而提高故障特征信号的信噪比。一般来说,可以通过硬滤波和软滤波技术来解决前述问题]。硬滤波指的是在将滤波器应用于数据采集之前,采样得到一个相对纯净的信号。而软滤波则是应用于数据采集之后,研究消噪算法来消除噪声,达到增强故障特征的目的。在实际工程应用中,通常采取的是在数据采集之前进行简单的滤波操作,而后利用消噪算法对采样后的数据进行二次消噪处理。传统的微弱信号检测方法主要有锁定放大、基于短时傅里叶变换的时频分析、盲源分离、取样积分与数字平均、自适应消噪等,新兴的方法主要有随机共振、Teager 能量算子、经验模态分解、共振稀疏分解、Wigner 高阶谱、混沌振子、小波变换等。
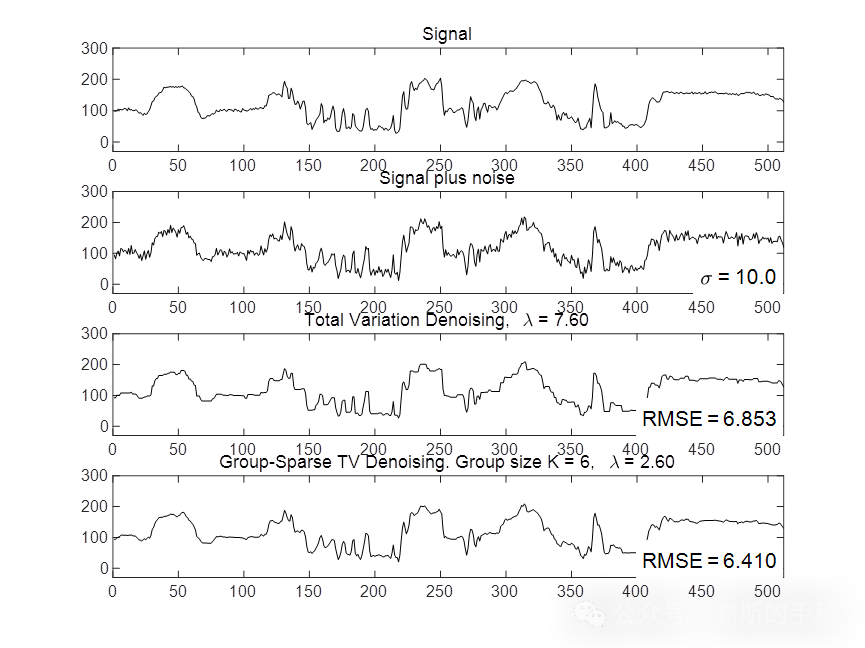
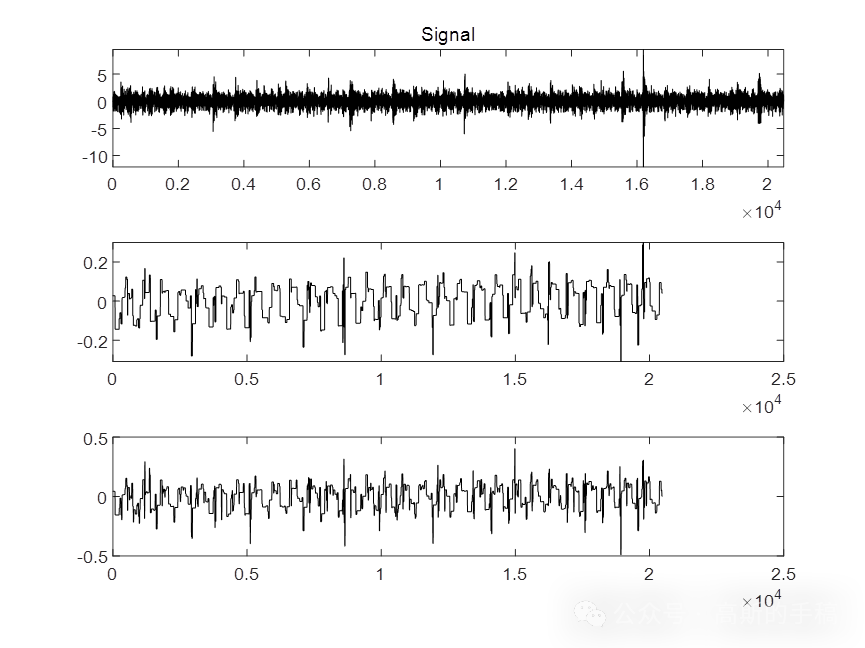
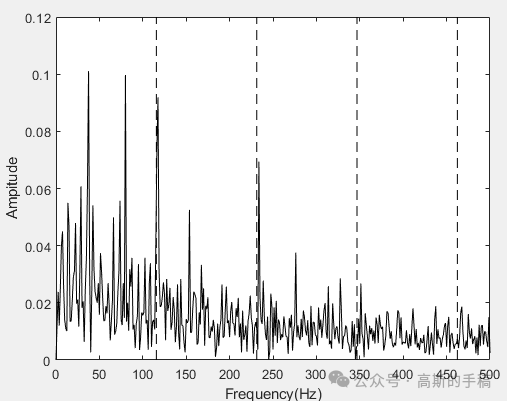
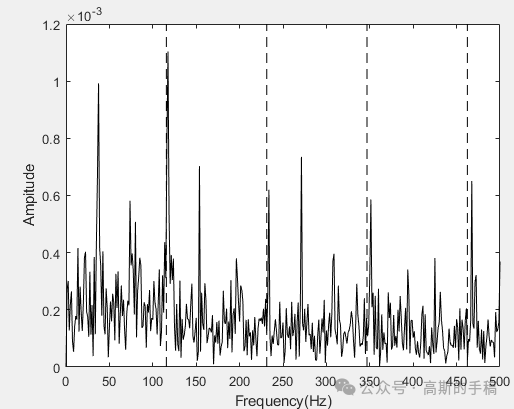
鉴于此,采用一种重叠群稀疏总变分信号降噪方法用于旋转机械故障诊断,运行环境为MATLAB R2018A。
function [x, cost] = tvd(y, lam, Nit)
% [x, cost] = tvd(y, lam, Nit)
% Total variation denoising (1D signals).
% The algorithm uses majorization-minimization
% and fast solver for banded linear systems.
%
% INPUT
% y - noisy signal
% lam - regularization parameter
% Nit - number of iterations
%
% OUTPUT
% x - denoised signal
% cost - cost function history
y = y(:); % Ensure column vector
cost = zeros(1, Nit); % Cost function history
N = length(y);
e = ones(N-1, 1);
DDT = spdiags([-e 2*e -e], [-1 0 1], N-1, N-1); % D*D' (sparse matrix)
D = @(x) diff(x); % D (operator)
DT = @(x) [-x(1); -diff(x); x(end)]; % D'
x = y; % Initialization
Dx = D(x);
Dy = D(y);
for k = 1:Nit
F = 1/lam * spdiags(abs(Dx), 0, N-1, N-1) + DDT; % F : Sparse matrix structure
% F = 1/lam * diag(abs(D(x))) + DDT; % Not stored as sparse matrix
x = y - DT(F\Dy); % Solve sparse linear system
Dx = D(x);
cost(k) = 0.5 * sum(abs(x-y).^2) + lam * sum(abs(Dx)); % Save cost function history
end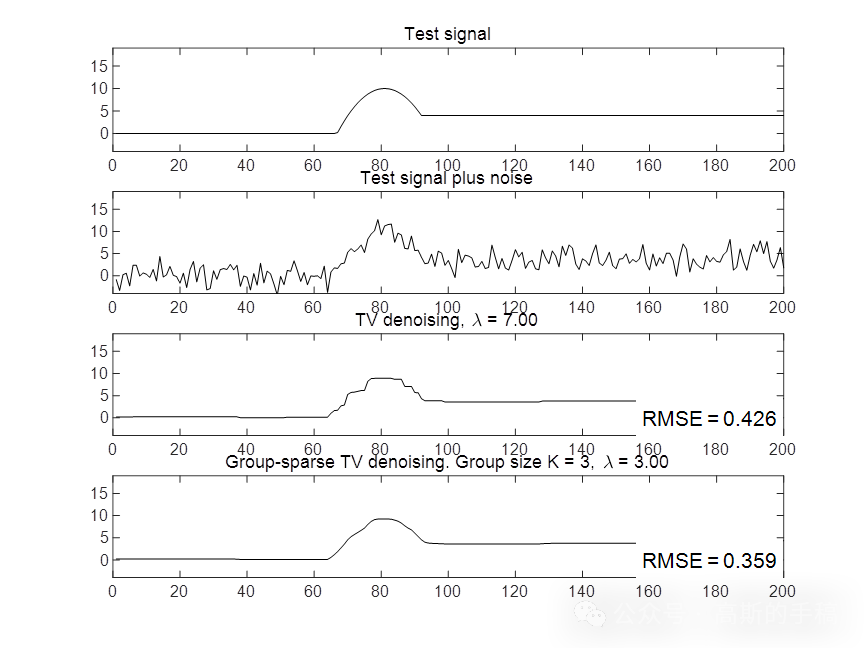
-
擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。 知乎学术咨询:https://www.zhihu.com/consult/people/792359672131756032?isMe=1 擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。