代码随想录-暑假算法第一天(数组篇)
1. 二分查找
力扣题目链接(opens new window)
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
1
2
3
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
1
2
3
提示:
- 你可以假设 nums 中的所有元素是不重复的。
- n 将在 [1, 10000]之间。
- nums 的每个元素都将在 [-9999, 9999]之间。
题解
class Solution {
public int search(int[] nums, int target) {
//左闭右闭区间
int left = 0;
int right = nums.length-1;
while(left <= right){
int middle = (left+right)/2;
if(nums[middle] > target){
right = middle-1;
}else if(nums[middle] < target){
left = middle + 1;
}else if(nums[middle] == target){
return middle;
}
}
//没有找到
return -1;
}
}
总结
-
属于基础题目,大家一看就懂了,主要是边界问题
-
大家可以使用左闭右闭区间来编写二分查找代码,left<=right,middle的值根据是左区间还是右区间来加减1
2. 移除元素
力扣题目链接(opens new window)
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并原地修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
示例 1: 给定 nums = [3,2,2,3], val = 3, 函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。 你不需要考虑数组中超出新长度后面的元素。
示例 2: 给定 nums = [0,1,2,2,3,0,4,2], val = 2, 函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。
你不需要考虑数组中超出新长度后面的元素。
暴力解法
这个题目暴力的解法就是两层for循环,一个for循环遍历数组元素 ,第二个for循环更新数组。
class Solution {
public int removeElement(int[] nums, int val) {
//暴力解法
int size = nums.length;
for(int i = 0;i<size;i++){
if(nums[i] == val){
//移除元素
for(int j= i+1;j<size;j++){
nums[j-1] = nums[j];
}
i--;
size--;
}
}
return size;
}
}
总结
-
特别要注意的是循环的条件,是size,而不是nums.length
-
本质就是for循环的双层嵌套
双指针(快慢指针)较为重要
双指针法(快慢指针法): 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
定义快慢指针
- 快指针:寻找新数组的元素 ,新数组就是不含有目标元素的数组
- 慢指针:指向更新 新数组下标的位置
很多同学这道题目做的很懵,就是不理解 快慢指针究竟都是什么含义,所以一定要明确含义,后面的思路就更容易理解了。
class Solution {
public int removeElement(int[] nums, int val) {
//快慢指针法 就是快
//慢指针
int slowIndex = 0;
//for循环
for(int i = 0;i < nums.length;i++){
//如果不相等
//快指针
int fastIndex = i;
if(nums[fastIndex] != val){
nums[slowIndex] = nums[fastIndex];
//慢指针移动
slowIndex++;
}
}
return slowIndex;
}
}
总结
-
定义两个指针,即快慢指针,慢指针用于指向新数组的元素,快指针用于遍历数组的全部元素
-
如果快指针指向的元素不等于val的值时,就把快指针所指向的数字赋值给慢指针所指向的数字
3.有序数组的平方
力扣题目链接(opens new window)
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
示例 1:
- 输入:nums = [-4,-1,0,3,10]
- 输出:[0,1,9,16,100]
- 解释:平方后,数组变为 [16,1,0,9,100],排序后,数组变为 [0,1,9,16,100]
示例 2:
- 输入:nums = [-7,-3,2,3,11]
- 输出:[4,9,9,49,121]
暴力解法
class Solution {
public int[] sortedSquares(int[] nums) {
for(int i= 0;i<nums.length;i++){
nums[i] = nums[i] * nums[i];
}
//进行排序
Arrays.sort(nums);
return nums;
}
}
总结
-
比较简单,就是一步一步的做,先进行平方,在进行排序
-
没有什么难点
双指针法
数组其实是有序的, 只不过负数平方之后可能成为最大数了。
那么数组平方的最大值就在数组的两端,不是最左边就是最右边,不可能是中间。
此时可以考虑双指针法了,i指向起始位置,j指向终止位置。
定义一个新数组result,和A数组一样的大小,让k指向result数组终止位置。
如果A[i] * A[i] < A[j] * A[j] 那么result[k--] = A[j] * A[j]; 。
如果A[i] * A[i] >= A[j] * A[j] 那么result[k--] = A[i] * A[i]; 。
class Solution {
public int[] sortedSquares(int[] nums) {
//因为是有序的,使用双指针法
//定义一个新的数组
int[] arr = new int[nums.length];
//因为要从小到大
int k = nums.length -1;
for(int i = 0,j= nums.length-1;i<=j;){
//进行判断
if(nums[i] * nums[i] > nums[j] * nums[j]){
//加入到新的数组里面
arr[k--] = nums[i] * nums[i];
i++;
}else{
//后面的平方大于前面平方的结果(包括相等的结果)
arr[k--] = nums[j] * nums[j];
j--;
}
}
return arr;
}
}
总结
-
定义一个大小相等的数组,用于存放元素,因为要从小到大,所以定义一个k,其值为数组的长度减一,即最大下标的元素的大小
-
定义两个指针,i,j分别指向头和尾,因为最大的那个数字只在头的位置或者尾巴的位置
-
进行判断,如果是前面的平方比后面的平方大,则把平方之后的数字的值添加到新的数组arr里面,然后k–( 从后往前填充),左区间要更新(i++),如果是后面的平方比前面的平方大,则反之,相等情况下也一样
4.长度最小的子数组
力扣题目链接(opens new window)
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组,并返回其长度。如果不存在符合条件的子数组,返回 0。
示例:
- 输入:s = 7, nums = [2,3,1,2,4,3]
- 输出:2
- 解释:子数组 [4,3] 是该条件下的长度最小的子数组。
提示:
- 1 <= target <= 10^9
- 1 <= nums.length <= 10^5
- 1 <= nums[i] <= 10^5
滑动窗口法(较为重要)
class Solution {
public int minSubArrayLen(int target, int[] nums) {
//滑动窗口法
int result = nums.length +1;
//j代表终止位置
int sum = 0;
for(int j = 0,i=0;j<nums.length;j++){
sum = sum + nums[j];
while(sum >= target){
//更新result
result = result > (j-i+1)? (j-i+1) : result;
//缩小窗口
sum = sum - nums[i];
//移动起始位置
i++;
}
}
return result == (nums.length+1) ? 0 : result;
}
}
总结
-
类似于一个可以滑动的窗口
-
j代表终止位置,依次遍历;sum控制窗口之间的数字的和;result控制符合条件的子数组的长度;i代表起始位置,当大于目标数字的时候,(缩小窗口,sum减去i指向的数字),移动i,
5.螺旋矩阵II
力扣题目链接(opens new window)
给定一个正整数 n,生成一个包含 1 到 n^2 所有元素,且元素按顺时针顺序螺旋排列的正方形矩阵。
示例:
输入: 3 输出: [ [ 1, 2, 3 ], [ 8, 9, 4 ], [ 7, 6, 5 ] ]
这道题目可以说在面试中出现频率较高的题目,本题并不涉及到什么算法,就是模拟过程,但却十分考察对代码的掌控能力。
要如何画出这个螺旋排列的正方形矩阵呢?
相信很多同学刚开始做这种题目的时候,上来就是一波判断猛如虎。
结果运行的时候各种问题,然后开始各种修修补补,最后发现改了这里那里有问题,改了那里这里又跑不起来了。
大家还记得我们在这篇文章数组:每次遇到二分法,都是一看就会,一写就废 (opens new window)中讲解了二分法,提到如果要写出正确的二分法一定要坚持循环不变量原则。
而求解本题依然是要坚持循环不变量原则。
模拟顺时针画矩阵的过程:
- 填充上行从左到右
- 填充右列从上到下
- 填充下行从右到左
- 填充左列从下到上
由外向内一圈一圈这么画下去。
可以发现这里的边界条件非常多,在一个循环中,如此多的边界条件,如果不按照固定规则来遍历,那就是一进循环深似海,从此offer是路人。
这里一圈下来,我们要画每四条边,这四条边怎么画,每画一条边都要坚持一致的左闭右开,或者左开右闭的原则,这样这一圈才能按照统一的规则画下来。
那么我按照左闭右开的原则,来画一圈,大家看一下:
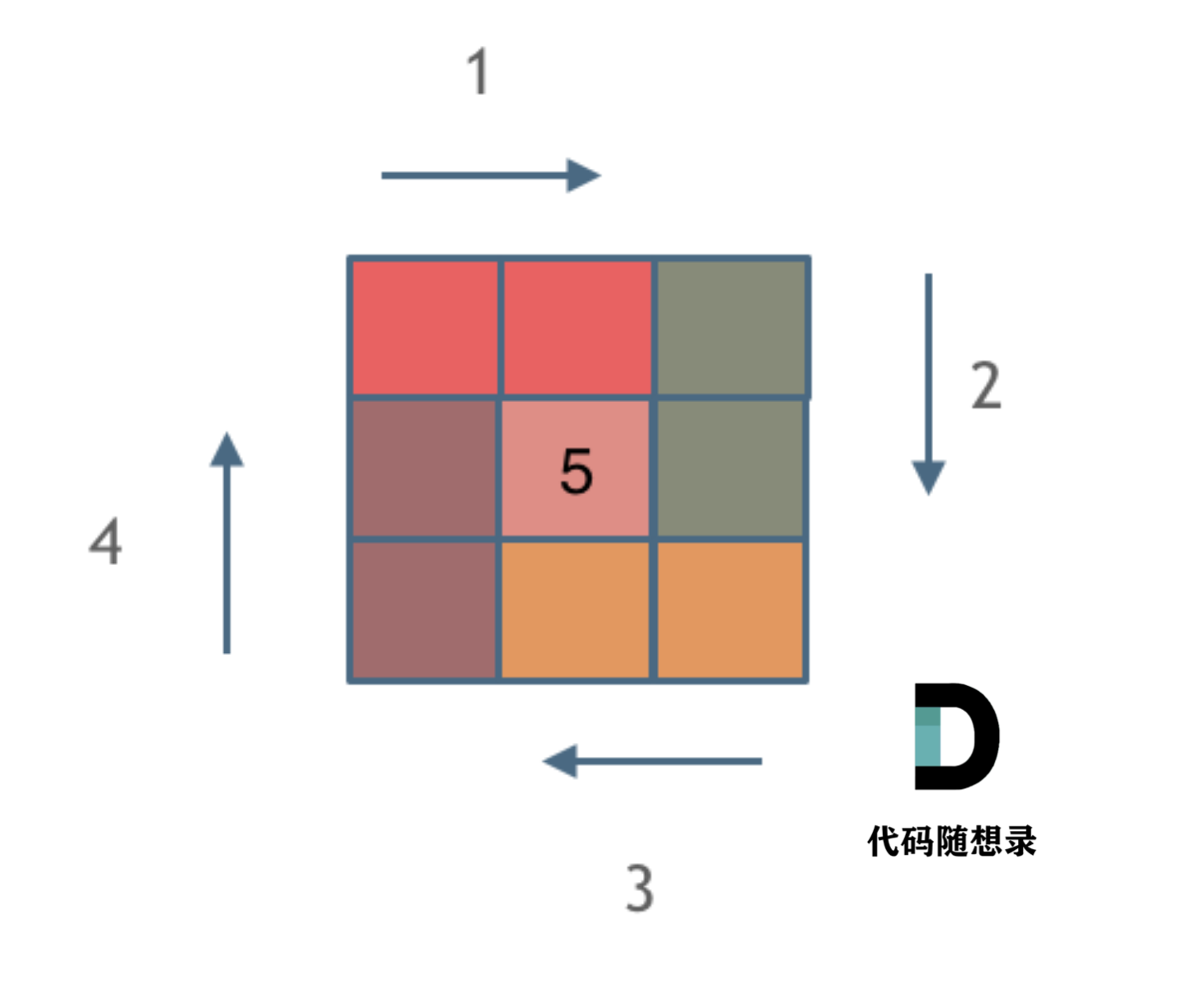
这里每一种颜色,代表一条边,我们遍历的长度,可以看出每一个拐角处的处理规则,拐角处让给新的一条边来继续画。
这也是坚持了每条边左闭右开的原则。
一些同学做这道题目之所以一直写不好,代码越写越乱。
就是因为在画每一条边的时候,一会左开右闭,一会左闭右闭,一会又来左闭右开,岂能不乱。
代码如下,已经详细注释了每一步的目的,可以看出while循环里判断的情况是很多的,代码里处理的原则也是统一的左闭右开。
题解1(我自己的做法一行一列法)较为容易理解
class Solution {
public int[][] generateMatrix(int n) {
//创建一个二维数组,存储数字
int[][] arr = new int[n][n];
int count = 1;
//头部
int top = 0;
//尾部
int bottom = n - 1;
//左部
int left = 0;
//右部
int right = n - 1;
while (count <= n * n) {
//从左往右
for (int i = left; i <= right; i++) {
arr[top][i] = count++;
}
top++;
//从上往下
for (int i = top; i <= bottom; i++) {
arr[i][right] = count++;
}
right--;
//从右往左
for (int i = right; i >= left; i--) {
arr[bottom][i] = count++;
}
bottom--;
//从下往上
for (int i = bottom; i >= top; i--) {
arr[i][left] = count++;
}
left++;
}
return arr;
}
}
总结
-
就只需要注意到当count为n*n的时候才能进入while,要不然会引起数组越界
-
法1: while的条件设为count < n*n,并且count初始值为0,之后++count;
-
法2: while的条件设为count<=n*n,并且count初始值为1,之后count++;
题解2(官方的解法左闭右开法)较为官方
class Solution {
public int[][] generateMatrix(int n) {
//创建一个二维数组,存储数字
int[][] arr = new int[n][n];
//规定左闭右开区间
//起始点
int startX = 0;
//int startY = 0;
//用于计数
int count = 1;
int i = 0;
int j = 0;
//记录圈数
int loop = 1;
//用于记录终止位置
int offset = 1;
while(loop <= n /2){
for(j = startX;j<n-offset;j++){
arr[startX][j] = count++;
}
for(i = startX;i<n-offset;i++){
arr[i][j] = count++;
}
for(;j>startX;j--){
arr[i][j] = count++;
}
for(;i>startX;i--){
arr[i][j] = count++;
}
//到下一圈,更新新的变量
loop++;
startX++;
//startY++;
offset++;
}
//奇数的特殊情况
if(n%2==1){
arr[n/2][n/2] = count++;
}
return arr;
}
}
总结
-
还是比较好理解的
-
规定一个标准(左闭右开),顺时针画一个圆,分为四次 ,每一次包头不包尾(左闭右开),while里面的条件是圈数,定义两个变量,分别控制(startX = 0)起始点和终点(offset = n -1);
-
当n为奇数时,需要额外判断,如果n为奇数,那么最后一圈,n是进入不到while循环里面的,需要在while循环结束后,手动添加最后一圈(arr[n/2][n/2] = ++count),count为计数器
数组总结篇
-
果然还是得多多练习,一看就会,一写就废
-
个人感觉数组篇难度不是很大,但是要注意的细节点很多,例如边界的判断…
-
在数组篇我学习了较为重要也非常有用的算法,例如二分法(在一个有序的数组里面查找指定的元素),双指针法,滑动窗口法,这些虽然现在可以已经懂了,但是要想完全理解,还是得多多编程
-
最后,开开心心的学习编程,充实的过好每一天编程已经成为了我生活的一部分了,











![[web]-代码审计-就这么直接](https://i-blog.csdnimg.cn/direct/8b0230c578e648178553e45305196c4b.png)





