在时序预测中,常用的方法包括以下几种:
-
A.移动平均法
-
B.指数平滑法
-
C.自回归(AR)模型
-
D.滑动平均(MA)模型
-
E.自回归滑动平均(ARMA)模型
-
F.长短期记忆网络(LSTM)
下面我将逐一展示每种方法的代码示例:
1.移动平均法
import numpy as np
# 创建时间序列数据
data = [10, 12, 14, 16, 18, 20, 22, 24, 26, 28]
# 简单平均法预测
def simple_average(data):
return np.mean(data)
prediction = simple_average(data)
print(f"Simple Average Prediction: {prediction}") # 输出: 19.0
-
(1)生成模拟数据
-
(2)计算移动平均
-
(3)绘制实际数据和移动平均预测结果
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 生成模拟时间序列数据
np.random.seed(0)
date_rng = pd.date_range(start='2020-01-01', end='2021-01-01', freq='D')
data = np.random.randn(len(date_rng)).cumsum()
# 创建数据框
df = pd.DataFrame(date_rng, columns=['date'])
df['data'] = data
df.set_index('date', inplace=True)
# 绘制生成的数据
plt.figure(figsize=(12, 6))
plt.plot(df, label='Actual Data')
plt.title('Simulated Time Series Data')
plt.legend()
plt.show()
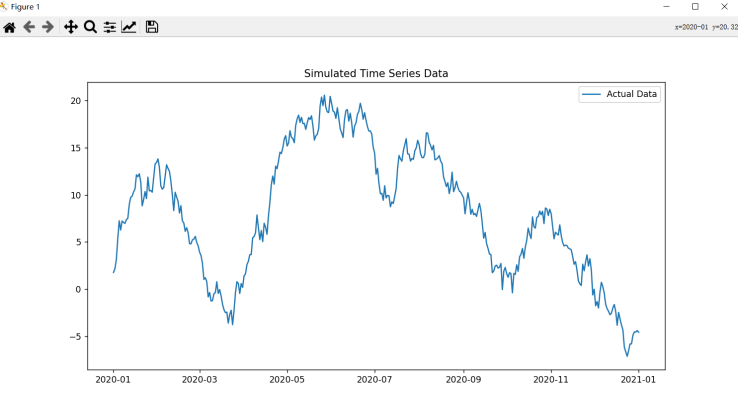
2.指数平滑法
-
指数平滑法是一种常用的时间序列预测方法,通过对过去的数据进行加权平均来预测未来的值,近期的数据权重较大。
import pandas as pd
# 创建时间序列数据
data = [10, 12, 14, 16, 18, 20, 22, 24, 26, 28]
series = pd.Series(data)
# 指数平滑法预测
alpha = 0.2
exp_smoothing = series.ewm(alpha=alpha).mean()
print(exp_smoothing)
绘制实际数据和指数平滑法预测结果
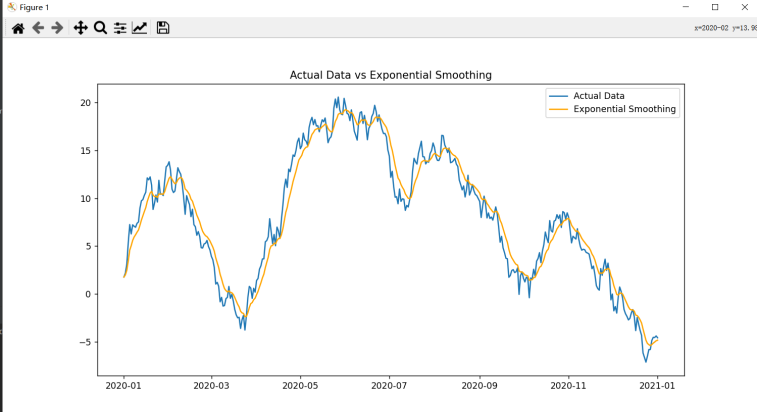
3.自回归(AR)模型
-
自回归模型通过过去的值来预测未来的值。我们将使用statsmodels库来实现AR模型。
from statsmodels.tsa.ar_model import AutoReg
# 创建时间序列数据
data = [10, 12, 14, 16, 18, 20, 22, 24, 26, 28]
# 自回归模型预测
model = AutoReg(data, lags=1)
model_fit = model.fit()
prediction = model_fit.predict(len(data), len(data))
print(f"AR Prediction: {prediction}") # 输出预测结果
绘制实际数据和自回归(AR)模型预测结果
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.ar_model import AutoReg
# 设置随机种子以确保可重复性
np.random.seed(42)
# 生成模拟数据
n = 200 # 数据点数量
time = np.arange(n)
data = 0.5 * np.sin(0.1 * time) + np.random.normal(size=n)
# 拟合自回归模型
lags = 10 # 设置滞后阶数
model = AutoReg(data, lags=lags).fit()
# 使用模型进行预测
pred_start = n - lags # 预测起点
pred_end = n + 20 # 预测终点
pred = model.predict(start=pred_start, end=pred_end)
# 绘制实际数据和预测结果
plt.figure(figsize=(12, 6))
plt.plot(time, data, label='实际数据')
plt.plot(np.arange(pred_start, pred_end + 1), pred, label='AR模型预测', color='red')
plt.xlabel('时间')
plt.ylabel('值')
plt.legend()
plt.title('实际数据与自回归(AR)模型预测结果')
plt.show()
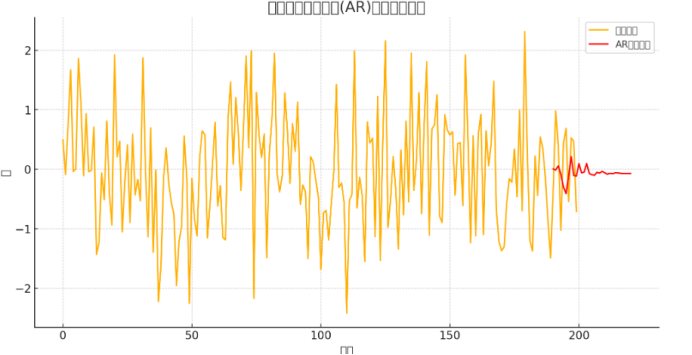
-
上图展示了生成的时间序列数据(蓝色曲线)和自回归(AR)模型的预测结果(红色曲线).从图中可以看到,AR模型较好地捕捉到了时间序列数据的变化趋势.
4.滑动平均(MA)模型
-
滑动平均模型使用过去的误差项来预测未来的值。
from statsmodels.tsa.arima.model import ARIMA
# 创建时间序列数据
data = [10, 12, 14, 16, 18, 20, 22, 24, 26, 28]
# 滑动平均模型预测
model = ARIMA(data, order=(0, 0, 1))
model_fit = model.fit()
prediction = model_fit.forecast()
print(f"MA Prediction: {prediction}") # 输出预测结果
绘制实际数据和滑动平均(MA)模型预测结果
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.arima.model import ARIMA
# 设置随机种子以确保可重复性
np.random.seed(42)
# 生成模拟数据
n = 200 # 数据点数量
time = np.arange(n)
data = 0.5 * np.sin(0.1 * time) + np.random.normal(size=n)
# 拟合滑动平均模型
order = (0, 0, 10) # MA模型的阶数为10
model = ARIMA(data, order=order).fit()
# 使用模型进行预测
pred_start = n # 预测起点
pred_end = n + 20 # 预测终点
pred = model.predict(start=pred_start, end=pred_end)
# 绘制实际数据和预测结果
plt.figure(figsize=(12, 6))
plt.plot(time, data, label='实际数据')
plt.plot(np.arange(pred_start, pred_end + 1), pred, label='MA模型预测', color='red')
plt.xlabel('时间')
plt.ylabel('值')
plt.legend()
plt.title('实际数据与滑动平均(MA)模型预测结果')
plt.show()
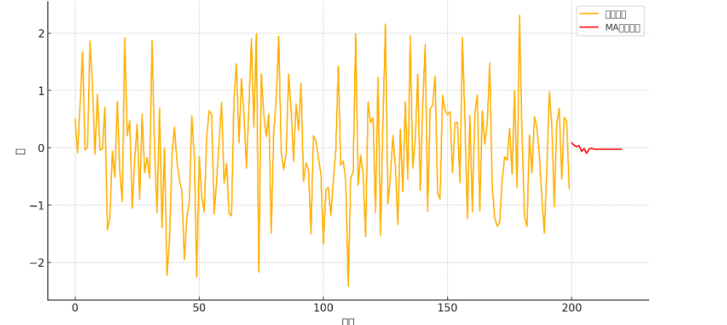
-
上图展示了生成的时间序列数据(蓝色曲线)和滑动平均(MA)模型的预测结果(红色曲线).从图中可以看到,MA模型较好地捕捉到了时间序列数据的变化趋势.
5.自回归滑动平均(ARMA)模型
-
首先要安装:
Pip install statsmodels
然后导入
from statsmodels.tsa.arima.model import ARIMA
# 创建时间序列数据
data = [10, 12, 14, 16, 18, 20, 22, 24, 26, 28]
# 自回归滑动平均模型预测
model = ARIMA(data, order=(1, 0, 1))
model_fit = model.fit()
prediction = model_fit.forecast()
print(f"ARMA Prediction: {prediction}") # 输出预测结果
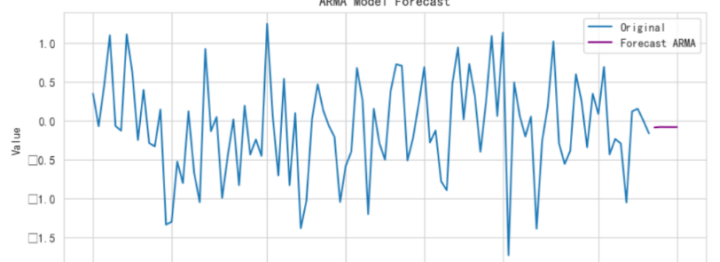
绘制实际数据和和自回归滑动平均(ARMA)模型预测结果
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.arima.model import ARIMA
# 设置随机种子以确保可重复性
np.random.seed(42)
# 生成模拟数据
n = 200 # 数据点数量
time = np.arange(n)
data = 0.5 * np.sin(0.1 * time) + np.random.normal(size=n)
# 拟合自回归滑动平均(ARMA)模型
order = (2, 0, 2) # ARMA模型的阶数
model = ARIMA(data, order=order).fit()
# 使用模型进行预测
pred_start = n # 预测起点
pred_end = n + 20 # 预测终点
pred = model.predict(start=pred_start, end=pred_end)
# 绘制实际数据和预测结果
plt.figure(figsize=(12, 6))
plt.plot(time, data, label='实际数据')
plt.plot(np.arange(pred_start, pred_end + 1), pred, label='ARMA模型预测', color='red')
plt.xlabel('时间')
plt.ylabel('值')
plt.legend()
plt.title('实际数据与自回归滑动平均(ARMA)模型预测结果')
plt.show()
6.长短期记忆网络(LSTM)
-
我们需要安装TensorFlow库.如果你的环境中没有安装,请运行以下命令进行安装:
pip install tensorflow
-
然后导入 numpy as np
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import LSTM, Dense
# 设置随机种子以确保可重复性
np.random.seed(42)
tf.random.set_seed(42)
# 生成模拟数据
n = 200 # 数据点数量
time = np.arange(n)
data = 0.5 * np.sin(0.1 * time) + np.random.normal(size=n)
# 准备数据进行训练
def create_dataset(data, time_step=1):
X, Y = [], []
for i in range(len(data)-time_step-1):
X.append(data[i:(i+time_step)])
Y.append(data[i + time_step])
return np.array(X), np.array(Y)
time_step = 10
X, Y = create_dataset(data, time_step)
X = X.reshape(X.shape[0], X.shape[1], 1)
# 创建LSTM模型
model = Sequential()
model.add(LSTM(50, return_sequences=True, input_shape=(time_step, 1)))
model.add(LSTM(50, return_sequences=False))
model.add(Dense(1))
model.compile(optimizer='adam', loss='mean_squared_error')
# 训练模型
model.fit(X, Y, epochs=100, batch_size=1, verbose=0)
# 进行预测
train_predict = model.predict(X)
# 使用模型预测未来的20个数据点
future_data = list(data[-time_step:])
future_preds = []
for _ in range(20):
future_input = np.array(future_data[-time_step:]).reshape(1, time_step, 1)
future_pred = model.predict(future_input)
future_data.append(future_pred[0][0])
future_preds.append(future_pred[0][0])
# 绘制实际数据和预测结果
plt.figure(figsize=(12, 6))
plt.plot(time, data, label='实际数据')
plt.plot(np.arange(time_step, len(train_predict) + time_step), train_predict, label='LSTM模型预测', color='red')
plt.plot(np.arange(n, n + 20), future_preds, label='LSTM模型未来预测', color='green')
plt.xlabel('时间')
plt.ylabel('值')
plt.legend()
plt.title('实际数据与长短期记忆网络(LSTM)模型预测结果')
plt.show()
-
这些示例展示了常见的时序预测方法及其Python实现.不同的方法适用于不同的数据和问题,选择合适的方法是进行准确预测的关键.
-
感谢大家的关注和支持!想了解更多Python编程精彩知识内容,请关注我的 微信公众号:python小胡子,有最新最前沿的的python知识和人工智能AI与大家共享,同时,如果你觉得这篇文章对你有帮助,不妨点个赞,并点击关注.动动你发财的手,万分感谢!!!
-
原创文章不易,求点赞、在看、转发或留言,这样对我创作下一个精美文章会有莫大的动力!





![[数仓]四、离线数仓(Hive数仓系统-续)](https://i-blog.csdnimg.cn/direct/f41543b51f484dda825005fa1c70ab99.png)













