本文文章较长,阅读时间约为5分钟,点击目录条目可以快速跳转

完成进度情况
2023年辽宁省大学生数学建模竞赛A题完整论文和代码目前我已经完成了,论文包括摘要、问题重述、问题分析、模型假设、符号说明、模型的建立和求解(问题1推力模型的建立和求解、问题2安全距离模型的建立和求解、问题3不同因素对安全标线设置的影响分析模型的建立和求解)、模型的评价等等,
另外B题完整论文和代码也已经写完了,包括摘要、问题重述、问题分享、模型假设、符号说明、模型的建立和求解(问题1无监督聚类模型的建立和求解,问题二有监督分类预测模型的建立和求解、问题三迁移预测模型的建立与适用性评估)、模型的评价、参考文献、附录
A题
一、 问题重述
2023年辽宁省数学建模竞赛A题铁路车站的安全标线题目如下:在火车站或地铁站台上,离站台边缘1米左右的地方都画有一条黄线(或白线),这是为什么呢?
这条线称为安全线(业内称之为安全标线),人们在候车时必须站在安全线以外的区域。这是因为列车高速行驶时,会带动附近的空气也发生高速运动。根据伯努利效应的解释,人面向列车这边的空气流速很大,气压就会减小,而背后的空气流速小,气压就大。这样,站台边的人就会受到一个从背后高压区向身体前低压区推的作用力,有可能造成人贴近列车而引发事故。
为此,《铁路技术管理规程》第157条明确规定,旅客列车停靠的高站台边缘距线路中心线的距离为1750mm,安全标线距站台边缘1000mm。非高站台安全标线与站台边缘距离为:列车通过速度不大于120km/h时,1000mm;列车通过速度120 km/h以上至160 km/h时,1500mm;列车通过速度160 km/h以上至200 km/h时,2000mm。
你的任务:
(1) 根据相关机理,考虑人的体重、体积以及和人的距离等影响因素,建立数学模型确定高铁或动车全速经过时,对站在站台人的“吸力”或“推力”的大小;
(2) 依据(1)的结果,建立数学模型,说明高铁、动车车站站台的安全标线的设置依据;
(3) 分析不同因素对安全标线设置的影响,依此,向铁路部门提供你的有关保障铁路站台安全的建议。
一、 摘要... 1
二、 问题重述... 3
三、 问题分析... 3
3.1 推力模型分析... 3
3.2 安全距离模型分析... 3
3.3 不同因素对安全标线设置的影响关系模型分析... 4
四、 模型假设... 4
4.1 推力模型的模型假设... 4
4.2 安全距离模型的模型假设... 5
五、 符号说明... 5
5.1 推力模型符号及说明... 5
5.2 安全距离模型符号及说明... 6
六、 模型的建立和求解... 6
6.1 问题一推力模型的建立... 6
6.2 问题一推力模型的求解... 7
6.2.1 物理仿真参数设置... 8
6.2.2 推力与速度的二维关系... 8
6.2.3 推力与速度、距离的三维关系... 9
6.2.4 推力与速度、体积的三维关系... 10
6.2.5 推力与距离、体积的三维关系图... 11
6.2.6 推力与速度、距离、体积的四维关系图... 12
6.3 问题二安全距离模型的建立... 14
6.4 问题二安全距离模型的求解... 15
6.4.1 物理仿真参数设置... 15
6.4.2 安全距离与速度的二维关系... 16
6.4.3 安全距离与速度、体重的三维关系... 17
6.4.4 安全距离与速度、体积的三维关系图... 18
6.4.5 安全距离与体重、体积的三维关系... 19
6.4.6 安全距离与速度、体重、体积的四维关系... 20
6.5 问题三模型的建立和求解... 22
6.5.1 不同因素对安全标线设置的影响... 22
6.5.2 给铁路部门的建议措施... 23
七、 模型的评价... 23
7.1 模型优缺点分析... 24
7.1.1 推力模型优缺点... 24
7.1.2 安全距离模型的优缺点... 24
7.2 模型展望... 25
二、 问题分析
辽宁省大学生数学建模竞赛A题各模型的分析过程如下:
2.1 推力模型分析
1. 伯努利效应考虑:首先,我们考虑伯努利效应,该效应描述了列车高速行驶时,站台上的人会受到由背后的高压区向前的低压区推的作用力。
2. 空气动力学参数引入:我们引入了空气动力学参数,包括空气密度(ρ)和空气动力学系数(C_d),这些参数用于计算站台人所受的推力。
3. 站台人的体积和站台与列车的距离:我们考虑了站台人的体积(V_p)和站台与列车的距离(D),以计算站台人的有效截面积(A)。
4. 推力公式:最终,我们使用伯努利效应和空气动力学参数,以及站台人的体积和站台与列车的距离,得出了推力的计算公式。
2.2 安全距离模型分析
(略,见评论)
2.3 不同因素对安全标线设置的影响关系模型分析
1. 列车速度影响:我们分析了列车速度对推力和安全距离的影响。较高的列车速度导致伯努利效应更加明显,会带来更大的推力。因此,需要设置更远离站台边缘的安全标线以适应高速列车。
2. 站台与列车的距离影响:我们分析了站台与列车的距离对推力和安全距离的影响。较短的距离会导致站台上的人受到更大的推力,因此需要确保站台与列车的距离足够大,以减小推力对站台上人的影响。
3. 站台人的体积影响:我们分析了站台人的体积对推力和安全距离的影响。站台人的体积直接影响了站台与列车的距离和安全标线的位置,因此需要综合考虑站台人的体积。
4. 摩擦系数和体重影响:我们分析了摩擦系数和站台人的体重对安全距离的影响。这些参数用于计算摩擦力,确保推力小于摩擦力,从而保证站台人的安全。
5. 空气动力学参数影响:我们提到了空气动力学参数,如空气密度和空气动力学系数,对推力和安全距离的影响。这些参数需要准确测量,以提高计算的准确性。
三、 模型假设
在本文中建立了两个不同的模型,一个是用于计算推力的模型,另一个是用于计算安全距离的模型。下面是这两个模型需要使用的主要模型假设:
3.1 推力模型的模型假设
1. 伯努利效应:模型假设了伯努利效应适用于列车高速行驶时,导致站台人受到背后高压区向身体前低压区推的作用力。
2. 空气动力学参数:模型假设了空气动力学参数,包括空气密度(ρ)和空气动力学系数(C_d),这些参数用于计算推力。
3. 站台人体积:模型假设了站台上的人的体积(V_p),并将其用于计算有效截面积(A)。
4. 列车速度:模型假设了列车速度(V)是一个重要的参数,对伯努利效应产生明显影响。
3.1 安全距离模型的模型假设
1. 摩擦力:模型假设了摩擦力是一个重要的安全因素,用于确定安全距离。摩擦力的计算采用了摩擦系数(μ)和站台人的体重(W)。
2. 推力:模型假设了推力是通过伯努利效应和空气动力学参数计算的,用于确定安全距离。
3. 空气动力学参数:类似于推力模型,安全距离模型也使用了空气动力学参数,包括空气密度(ρ)和空气动力学系数(C_d)。
4. 站台人的体积:模型假设了站台上的人的体积(V_p),并将其用于计算有效截面积(A)。
5. 站台与列车的距离:模型假设了站台与列车的距离(D)是一个重要的参数,影响了推力和安全距离的计算。
六、 模型的建立和求解
6.1 问题一推力模型的建立
要建立数学模型来确定高铁或动车全速经过时对站在站台的人的“吸力”或“推力”,可以考虑伯努利效应、空气动力学、重力和站台人体的参数。以下是一个简化的模型,其中考虑了空气的流动、站台人的体重和体积以及站台与列车的距离。
模型假设:
列车速度:V (km/h)
站台人的体重:W (N)
站台人的体积:V_p (m^3)
站台与列车的距离:D (m)
空气密度:ρ (kg/m^3)
空气动力学系数:C_d(这是一个复杂的参数,取决于站台和列车的具体几何形状,可进一步细化建模,建了的话你的模型更加全面)
根据伯努利方程,站台人面向列车的一侧,空气流速较大,气压较低。站台人身后的空气流速较小,气压较高。这将导致站台人受到一个从背后向前推的作用力,即推力。
推力可以用以下公式来估算,(略),A 是站台人的有效截面积 ,
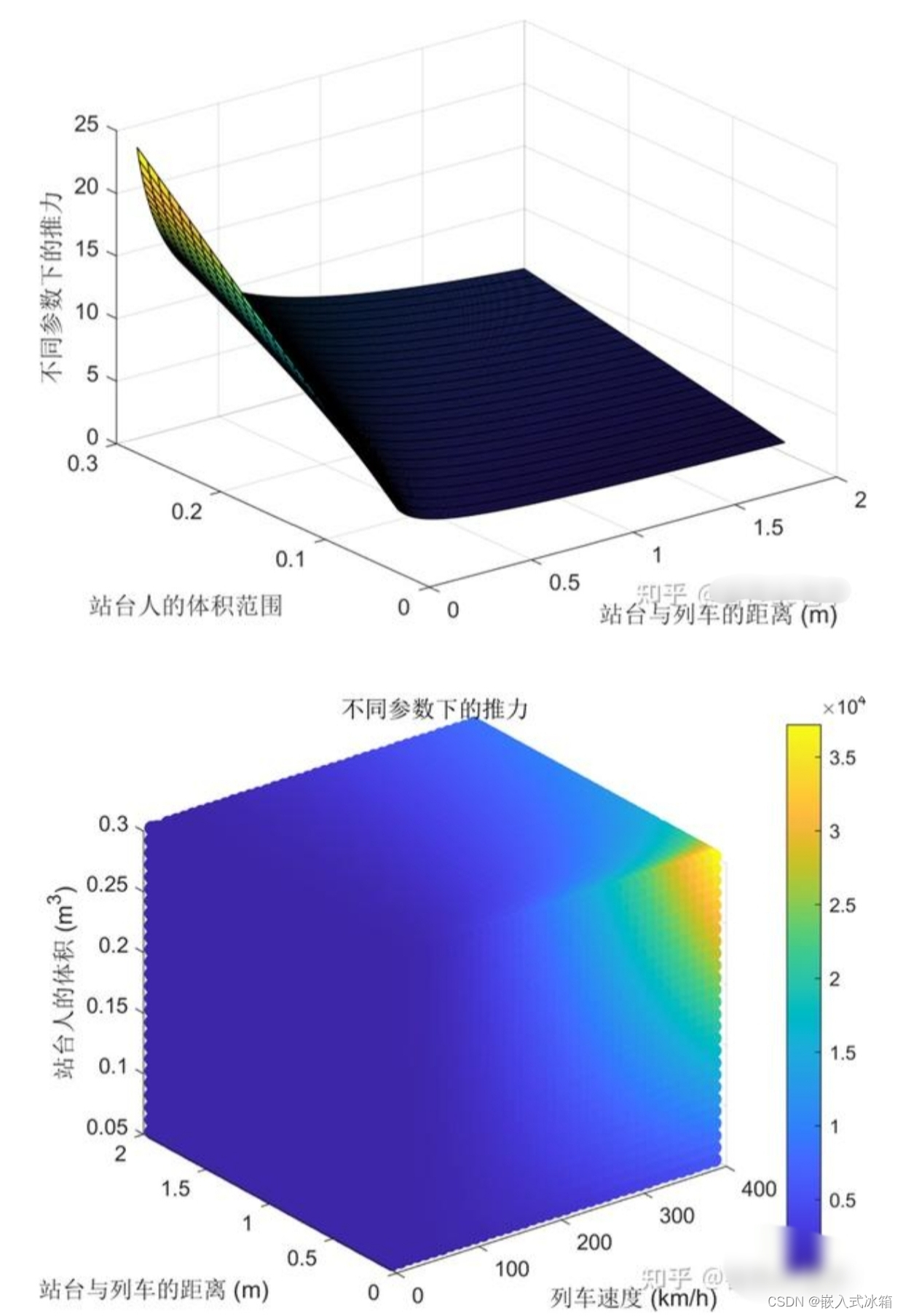
6.5 问题三模型的建立和求解
问题3根据前面的求解结果进行语文建模即可。
安全标线的设置对铁路站台的安全至关重要,因此需要综合考虑各种因素来确保乘客的安全。以下是不同因素对安全标线设置的影响以及向铁路部门提供的建议
给铁路部门的建议措施
综合上述因素,建议铁路部门进行以下措施来保障铁路站台的安全:
1. 进行详尽的工程设计:确保站台与列车的距离充分考虑列车速度、人的体积、摩擦系数等因素,以减小推力的影响。
2. 定期检查和维护:定期检查站台和列车的结构,以确保站台边缘的安全标线位置符合规范。
3. 教育和提醒乘客:铁路部门可以通过广播、标牌和工作人员提醒乘客站在安全标线以外的区域,以减小事故的风险。
4. 研究和改进:进行研究和模拟分析,以改进安全标线的设置,以适应不同列车类型和站台设计。
5. 合理安排站台人流:在高峰时段采取措施,以平衡站台上的人流,减少拥挤,减小事故发生的可能性。
B题
摘要略,具体见评lun区
二、 问题重述
2023辽宁省数学建模竞赛B题:“海洋强国”战略部署已成为推动中国现代化建设的重要组成部分,国家对此提出“发展海洋经济,保护海洋生态环境,加快建设海洋强国”的明确要求。 《辽宁省“十四五”海洋经济发展规划》明确未来全省海洋经济的发展战略、发展目标、重大任务、空间部署和保障措施。规划范围包括辽宁省全部海域和大连、丹东、锦州、营口、盘锦和葫芦岛6 个市以及海洋经济发展所依托的相关陆域,规划期限为2021 年至2025 年,展望到2035 年。辽宁省作为中国最北沿海省份,拥有2292.4 公里海岸线(如图1 所示)。
在“海洋强省”建设目标的背景下,完成海洋经济发展规划的目标重在海洋高新技术领域创新。其中关键核心技术之一是攻克水下导航与定位的适配区分类预测技术。
水下航行器在执行水下任务时需要保持自主、无源、高隐蔽性、不受地域和时域限制、高精度的导航与定位。重力辅助导航是满足上述条件的主要方法之一。 在重力辅助导航系统中,影响导航可靠性与精度的关键步骤是选择匹配性高的航行区域,即适配区。适配区的标定与识别技术是最具挑战性的问题之一。选取适配区前需要对研究海域的重力基准图(基础性的是重力异常基准图)进行插值加密处理,基于重力基准图所提供水下航行器航行区域的重力异常变化情况对适配区的选取进行分析。
重力异常(值)的定义为:实际地球内部的物质密度分布不均匀,导致实际观测重力值与理论上的正常重力值总存在偏差,在排除各种干扰因素影响后,仅仅由地球物质密度分布不匀所引起的重力的变化,简称为重力异常。
在重力异常变化显著区域,导航系统可获得高的定位精度;反之,在重力异常变化平坦区域,导航系统会出现定位精度的不敏感。由于不同区域的重力异常特征分布不同,建立可行的适配区分类预测模型,对保障水下航行器的导航精度至关重要。
假设X 为影响区域匹配性的特征属性指标,Y 为刻画区域适配性的输出结果, F 为以X 为输入以Y 为输出的分类预测系统。
基于上述背景分析,请参考附件中的重力异常数据建立数学模型,解决以下问题:
问题一:附件1,给出一组分辨率为1’×1’(相邻两格网点间的距离是1’)的重力异常基准数据A,试通过精细化基准图,合理划分区域,完成各区域的适配性标定(标签Y )。
问题二:根据问题一中各划分区域的适配性标定结果Y ,合理选择区域的特征属性指标(特征X ),试建立有效的区域适配区分类预测模型(系统F )。
问题三:利用附件二中的重力异常基准数据B,试对问题二所建立的系统F进行迁移性预测并讨论该系统F 对新重力异常数据的适用性。
目录:
一、 摘要.... 1
二、 问题重述.... 3
三、 问题分析.... 4
3.1 问题一分析..... 4
3.2 问题二分析..... 4
3.3 问题三分析..... 4
四、 模型假设.... 5
五、 符号说明.... 6
六、 模型的建立和求解.... 6
6.1 问题一模型的建立和求解.... 6
6.1.1数据可视化.... 6
6.1.2 K均值聚类方法:.... 7
6.1.3 聚类求解结果.... 10
6.2 问题二模型的建立和求解.... 11
6.2.1 随机森林算法.... 11
6.2.2 决策树算法.... 12
6.2.3 SVM算法.... 13
6.2.4 使用其他多种分类方法.... 16
6.2.5 不同模型的比较.... 17
6.3 问题三模型的建立和求解.... 19
6.3.1 重力异常数据进行可视化.... 19
6.3.2 迁移预测.... 20
6.3.3 重力异常数据的适用性评估.... 21
七、 模型的评价.... 22
7.1 模型的优缺点.... 22
三、 问题分析
要建立一个数学模型来解决2023辽宁省数学建模竞赛B题,可以采用机器学习或统计分析的方法来完成重力异常数据的区域适配性标定。步骤如下:
3.1 问题一分析
数据准备:
导入附件1中的数据(经度、纬度、重力异常值)。 可能需要对数据进行预处理,如数据清洗,处理缺失值,进行标准化等。 特征工程:
可以考虑根据经度和纬度创建额外的特征,如距离某个地理坐标点的距离等。
标定区域适配性标签Y:
为了标定区域的适配性标签Y,需要定义一种方法来将数据点分为不同的区域或类别。这是一个无监督学习问题,可以考虑使用聚类分析(如K均值聚类)来将数据点分成不同的区域。
3.2 问题二分析
分类预测模型建立:
选择合适的机器学习模型,如决策树、随机森林、支持向量机、神经网络等,来预测区域适配性标签Y。 划分数据集为训练集和测试集,用训练集来训练模型,然后用测试集来评估模型的性能。 模型评估:
使用合适的性能指标(如准确度、召回率、F1分数等)来评估模型的性能。 可能需要进行交叉验证以确保模型的稳定性和泛化能力。
3.3 问题三分析
模型应用:
一旦模型建立并评估成功,可以使用该模型来预测附件2中的重力异常数据的区域适配性标签Y。
四、 模型假设
五、 符号说明
以下是问题1、问题2和问题3中需要使用的模型符号及其说明的总结
六、 模型的建立和求解
6.1 问题一模型的建立和求解
6.1.1 数据可视化
使用Python的matplotlib库对2023辽宁省数学建模竞赛B题数据驱动的水下导航适配区分类预测问题一进行数据可视化,然后使用K均值聚类进行数据点分区。
# 设置中文字体 plt.rcParams['font.sans-serif'] = 'SimHei' # 使用中文字体(这里使用的是“黑体”) plt.rcParams['axes.unicode_minus'] = False # 用于正常显示负号 # 读取数据 # 可视化数据 plt.scatter(data['经度'], data['纬度'], c=data['重力异常值'], cmap='viridis') plt.xlabel('经度') plt.ylabel('纬度') plt.title('重力异常数据分布') plt.colorbar(label='重力异常值') plt.savefig('gravity_anomaly_visualization.png', dpi=300) plt.show()
6.1.2 K均值聚类方法
K均值聚类是一种无监督学习方法,用于将数据点分成K个不同的簇,以使每个数据点属于最近的簇。该方法的目标是最小化数据点与其所属簇中心之间的距离的总和。K均值聚类的算法如下:
选择K个初始簇中心,可以随机选择或根据某种启发式方法选择。
将每个数据点分配到与其最近的簇中心。
更新每个簇的中心,计算每个簇中所有数据点的平均值。
重复步骤2和步骤3,直到簇中心不再发生显著变化或达到预定的迭代次数。
# 使用K均值聚类 X = data[['经度', '纬度', '重力异常值']] scaler = StandardScaler() X_scaled = scaler.fit_transform(X) # 标准化数据 # 设置聚类数(这里设置为3,你可以根据实际情况调整) kmeans = KMeans(n_clusters=3, random_state=0) # 保存包含区域标签的数据 data.to_excel('附件1_重力异常数据带区域标签.xlsx', index=False)
6.1.3 聚类求解结果
# 读取带有区域标签的数据 data = pd.read_excel('附件1_重力异常数据带区域标签.xlsx') # 获取不同区域的数据 region1 = data[data['区域标签'] == 0] region2 = data[data['区域标签'] == 1] region3 = data[data['区域标签'] == 2] # 可视化不同区域的数据 plt.scatter(region1['经度'], region1['纬度'], label='区域1', c='red', marker='o') plt.scatter(region2['经度'], region2['纬度'], label='区域2', c='blue', marker='s') plt.scatter(region3['经度'], region3['纬度'], label='区域3', c='green', marker='^')
上述代码将可视化数据分布,并将其保存为名"gravity_anomaly_visualization.png"的图像。然后,它使用K均值聚类将数据点分为3个不同的区域,并将带有区域标签的数据保存为一个新的Excel文件。可以根据需要更改聚类数或其他参数以获得更合适的结果。
1.1 问题二模型的建立和求解
2023辽宁省数学建模B题问题二:根据问题一中各划分区域的适配性标定结果Y ,合理选择区域的特征属性指标(特征X ),试建立有效的区域适配区分类预测模型(系统F )。
为了建立一个有效的区域适配区分类预测模型,可以采用监督学习方法,例如决策树、随机森林、支持向量机等,来预测区域的适配性标定结果Y