1、基于浅层神经网络的数据拟合的简介、原理以及matlab实现
1)内容说明
基于浅层神经网络的数据拟合是一种常见的机器学习方法,用于通过输入数据来拟合一个非线性函数。这种方法通常包括一个输入层、一个或多个隐藏层和一个输出层。神经网络通过学习权重参数来逐步优化模型,使其能够更好地拟合训练数据。
神经网络的原理是通过前向传播将输入数据传递到隐藏层和输出层,然后通过反向传播来更新权重参数,以减小预测误差。在每次迭代中,通过计算损失函数的梯度来更新权重,并不断优化模型,直到达到预定的停止条件。
在MATLAB中,可以使用神经网络工具箱来实现基于浅层神经网络的数据拟合。首先,需要定义网络结构、选择激活函数、设置训练参数等。然后,使用训练数据来训练神经网络模型,并利用测试数据来评估模型的性能。
总的来说,基于浅层神经网络的数据拟合是一种强大的机器学习方法,可以用于解决回归、分类等问题。通过不断优化参数,神经网络可以更好地拟合数据,提高预测准确性。
2)算法说明
莱文贝格-马夸特算法
莱文贝格-马夸特(Levenberg-Marquardt)算法是一种用于求解非线性最小二乘问题的优化算法。该算法结合了最速下降方法(Levenberg算法)和高斯-牛顿方法(Marquardt算法)的优点,旨在找到最小化目标函数的参数值。
在神经网络中,莱文贝格-马夸特算法通常用于训练反向传播神经网络中的权重参数。该算法通过对神经网络的损失函数进行最小化,使得神经网络的输出与实际观测值更加接近。莱文贝格-马夸特算法在神经网络训练过程中具有较快的收敛速度和较好的稳定性。
莱文贝格-马夸特算法的基本思想是通过不断地调整参数的值,使得目标函数的值逐渐减小。该算法结合了梯度下降和牛顿法的优点,可以更快地收敛到最优解,并对参数的初始值不敏感。在每一步迭代中,莱文贝格-马夸特算法会根据当前的参数值计算一个近似的海森矩阵,然后通过调整步长来更新参数值,直到达到最优解或收敛到一个局部极小值。
总体来说,莱文贝格-马夸特算法是一种强大且高效的优化算法,特别适用于解决非线性最小二乘问题,如神经网络权重训练中的参数优化。通过使用莱文贝格-马夸特算法,可以加快神经网络的训练速度并提高性能,从而更好地拟合和预测数据。
贝叶斯正则化
贝叶斯正则化是一种基于贝叶斯统计理论的参数估计方法,用于处理参数估计中的过拟合问题。在机器学习和统计建模中,经常会遇到模型过于复杂,导致在训练数据上表现良好但在测试数据上泛化能力不足的情况,这就是过拟合。贝叶斯正则化通过引入先验概率对参数进行约束,降低模型的复杂度,从而提高模型的泛化能力。
在贝叶斯正则化中,参数估计的过程是一个加权考虑数据拟合和先验信息的过程。贝叶斯正则化采用贝叶斯推断的方法,通过最大化后验概率来获得参数的估计值。在构建模型时,需要为参数引入一个先验概率分布,表示对参数的先验知识或假设,然后通过贝叶斯定理将先验信息与观测数据结合,得到参数的后验分布,进而进行参数估计。
一种常见的贝叶斯正则化技术是贝叶斯岭回归(Bayesian Ridge Regression),其中使用岭回归的L2范数作为先验概率,通过最大化后验概率来求解参数。贝叶斯岭回归可以在保持模型简单性的同时提高模型的泛化能力,有效地解决过拟合问题。
总的来说,贝叶斯正则化是一种有助于解决过拟合问题的参数估计方法,通过引入先验概率对参数进行约束,提高模型的泛化能力。贝叶斯正则化在机器学习和统计建模中得到广泛应用,帮助提高模型的性能和鲁棒性。
量化共轭梯度
量化共轭梯度(Quantum Gradient Descent)是一种基于量子计算和梯度下降结合的优化算法。量子计算是利用量子力学原理进行信息处理和计算操作的新型计算模式,其中量子比特的特性可以实现高效的并行计算和处理。
在量子共轭梯度算法中,梯度下降的更新步骤会结合经典的梯度信息和量子计算的优势,实现更高效的优化过程。通过利用量子比特的叠加态和量子纠缠的性质,在每一步迭代中可以进行更加复杂和高效的计算运算,从而加速收敛速度和提高优化结果的精度。
量子共轭梯度算法的核心思想是利用量子计算的优势来加速梯度下降算法的收敛过程,从而在解决大规模问题和高维度数据时提供更好的性能。该算法结合了经典梯度下降算法和量子计算的优势,可以在一定程度上实现比传统梯度下降算法更快的优化速度。
需要注意的是,量子共轭梯度算法目前处于研究阶段,仍然需要进一步的实践和发展以验证其在不同领域的有效性和实用性。随着量子计算技术的不断发展和进步,量化共轭梯度算法有望在未来成为优化问题中的重要工具之一。
2、加载数据
1)说明
将预测变量 bodyfatInputs 和响应变量 bodyfatTargets 加载到工作区
将体脂预测变量加载到数组 x 中,将体脂响应变量加载到数组 t 中。
2)代码
%将预测变量 bodyfatInputs 和响应变量 bodyfatTargets 加载到工作区
load bodyfat_dataset
%将体脂预测变量加载到数组 x 中,将体脂响应变量加载到数组 t 中。
[x,t] = bodyfat_dataset;3、选择训练算法
1)说明
使用默认的莱文贝格-马夸特算法 (trainlm) 进行训练。
也可将网络训练函数设置为贝叶斯正则化 (trainbr) 或量化共轭梯度 (trainscg)
2)代码
%使用默认的莱文贝格-马夸特算法 (trainlm) 进行训练。
%也可将网络训练函数设置为贝叶斯正则化 (trainbr) 或量化共轭梯度 (trainscg)
trainFcn = 'trainlm'; % Levenberg-Marquardt反向传播。4、创建网络
1)说明
用于函数拟合(或回归)问题的默认网络 fitnet 是一个前馈网络,其默认 tan-sigmoid 传递函数在隐藏层,线性传递函数在输出层。网络有一个包含十个神经元(默认值)的隐藏层。网络有一个输出神经元,因为只有一个响应值与每个输入向量关联。
2)代码
%用于函数拟合(或回归)问题的默认网络 fitnet 是一个前馈网络,其默认 tan-sigmoid 传递函数在隐藏层,线性传递函数在输出层。网络有一个包含十个神经元(默认值)的隐藏层。网络有一个输出神经元,因为只有一个响应值与每个输入向量关联。
hiddenLayerSize = 10;
net = fitnet(hiddenLayerSize,trainFcn);5、划分数据
1)说明
预测变量向量和响应向量将被随机划分,70% 用于训练,15% 用于验证,15% 用于测试
2)代码
net.divideParam.trainRatio = 70/100;
net.divideParam.valRatio = 15/100;
net.divideParam.testRatio = 15/100;6、训练及查看网络
1)说明
训练查看网络
2)代码
[net,tr] = train(net,x,t);
view(net)3)试图效果
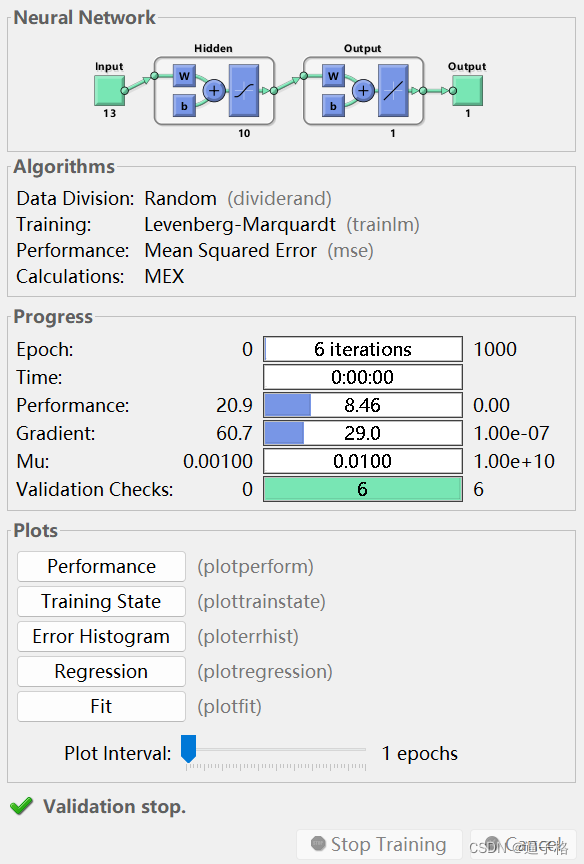
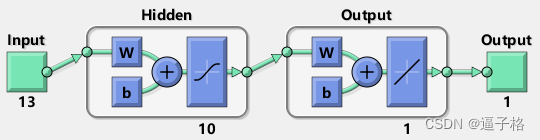
7、测试网络
1)使用经过训练的网络来计算网络输出
说明:使用经过训练的网络来计算网络输出。计算网络输出、误差和整体性能。
代码
y = net(x);
e = gsubtract(t,y);
performance = perform(net,t,y)
performance =
19.87832)测试索引
代码
tInd = tr.testInd;
tstOutputs = net(x(:,tInd));
tstPerform = perform(net,t(tInd),tstOutputs)
tstPerform =
13.12303)神经网络数据拟合结果视图分析
均方差图
说明:
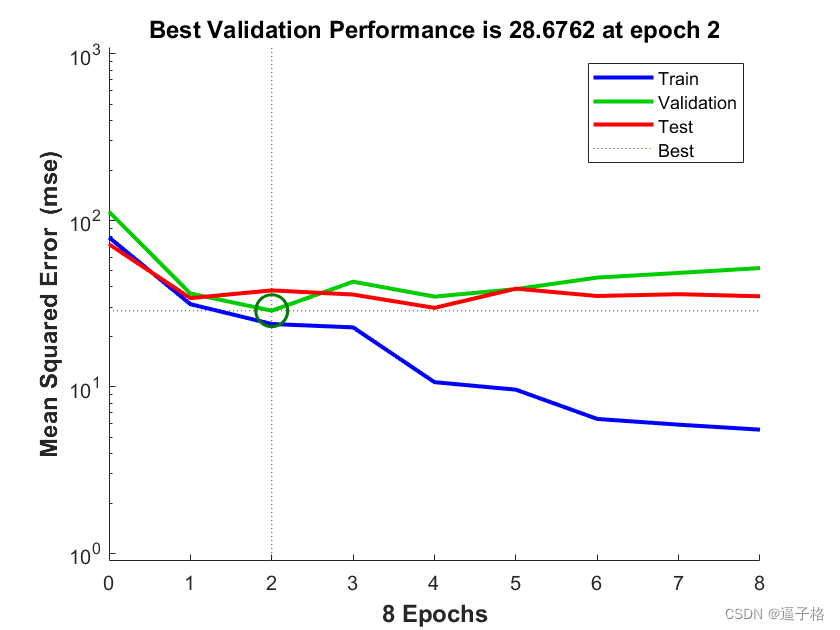
训练状态图
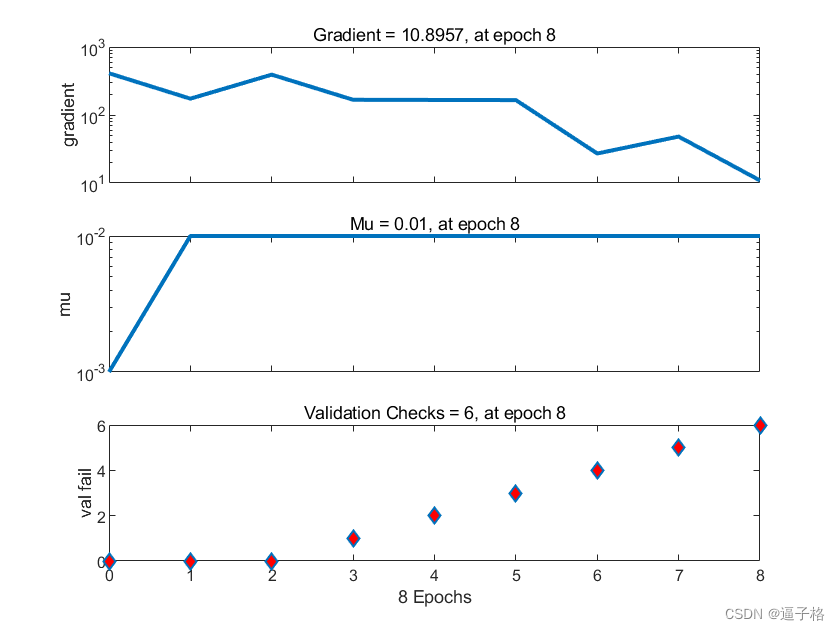
误差分布图
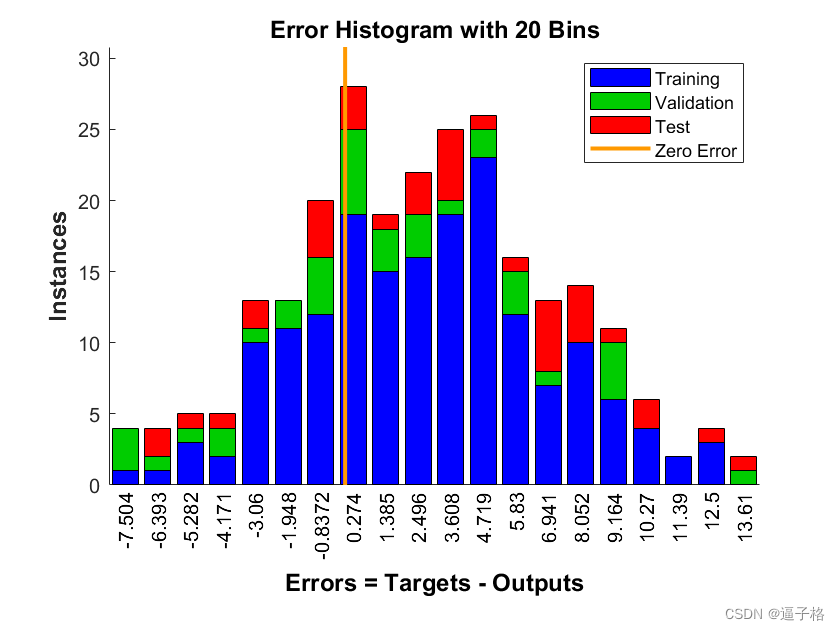
回归图
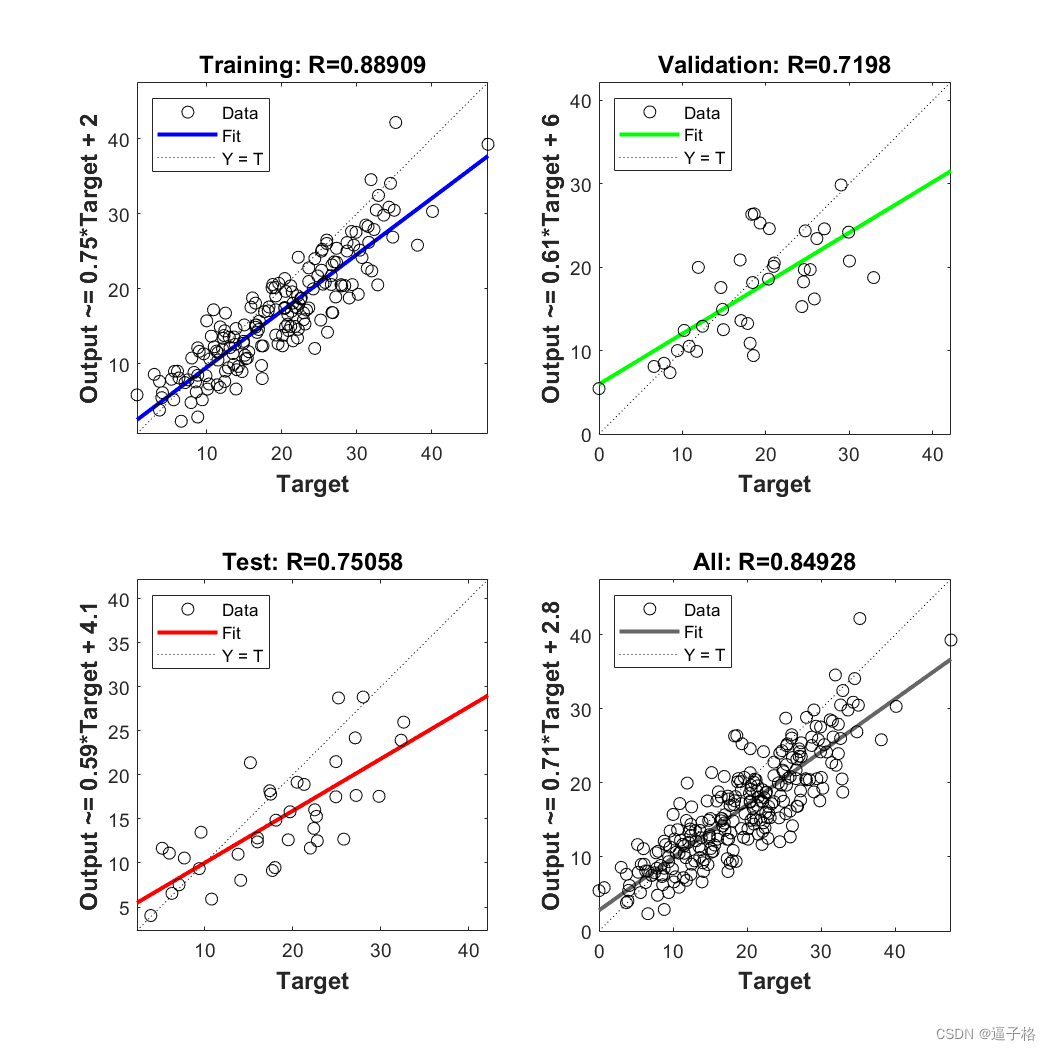
8、总结
基于浅层神经网络的数据拟合在MATLAB中的实现主要包括以下几个步骤:
-
数据准备:首先,需要准备训练数据和测试数据。确保数据已经经过预处理和标准化,以便神经网络更好地学习和拟合。
-
网络设计:定义神经网络的结构,包括输入层、隐藏层和输出层的神经元数量、激活函数等。可以选择不同类型的网络结构,如全连接神经网络、卷积神经网络等。
-
模型训练:使用训练数据来训练神经网络模型。可以选择不同的优化算法和损失函数,如梯度下降算法和均方误差损失函数。通过多次迭代更新权重参数,使模型能够更好地拟合数据。
-
模型评估:使用测试数据来评估训练好的模型的性能。可以计算预测精度、误差率等指标,以评估模型的准确性和泛化能力。
-
参数调优:根据模型评估结果,可以对神经网络的模型参数进行调优,如调整神经元数量、隐藏层层数、学习率等,以进一步提高模型性能。
通过以上步骤,可以使用MATLAB实现基于浅层神经网络的数据拟合,使得模型能够更好地学习和预测数据,从而解决各种回归、分类等问题。神经网络在数据拟合中的应用非常广泛,能够处理复杂的非线性关系,适用于各种领域的数据分析和预测任务。
9、源代码
代码
%% 基于浅层神经网络的数据拟合
%% 加载数据
%将预测变量 bodyfatInputs 和响应变量 bodyfatTargets 加载到工作区
load bodyfat_dataset
%将体脂预测变量加载到数组 x 中,将体脂响应变量加载到数组 t 中。
[x,t] = bodyfat_dataset;
%% 选择训练算法
%使用默认的莱文贝格-马夸特算法 (trainlm) 进行训练。
%也可将网络训练函数设置为贝叶斯正则化 (trainbr) 或量化共轭梯度 (trainscg)
trainFcn = 'trainlm'; % Levenberg-Marquardt反向传播。
%% 创建网络
%用于函数拟合(或回归)问题的默认网络 fitnet 是一个前馈网络,其默认 tan-sigmoid 传递函数在隐藏层,线性传递函数在输出层。网络有一个包含十个神经元(默认值)的隐藏层。网络有一个输出神经元,因为只有一个响应值与每个输入向量关联。
hiddenLayerSize = 10;
net = fitnet(hiddenLayerSize,trainFcn);
%% 划分数据
%预测变量向量和响应向量将被随机划分,70% 用于训练,15% 用于验证,15% 用于测试
net.divideParam.trainRatio = 70/100;
net.divideParam.valRatio = 15/100;
net.divideParam.testRatio = 15/100;
%% 训练及查看网络
[net,tr] = train(net,x,t);
view(net)
%% 测试网络
%使用经过训练的网络来计算网络输出。计算网络输出、误差和整体性能。
y = net(x);
e = gsubtract(t,y);
performance = perform(net,t,y)
%测试索引
tInd = tr.testInd;
tstOutputs = net(x(:,tInd));
tstPerform = perform(net,t(tInd),tstOutputs)