系列文章目录及链接
上篇:机器学习(五) -- 监督学习(7) --SVM1
下篇:
前言
tips:标题前有“***”的内容为补充内容,是给好奇心重的宝宝看的,可自行跳过。文章内容被“文章内容”删除线标记的,也可以自行跳过。“!!!”一般需要特别注意或者容易出错的地方。
本系列文章是作者边学习边总结的,内容有不对的地方还请多多指正,同时本系列文章会不断完善,每篇文章不定时会有修改。
由于作者时间不算富裕,有些内容的《算法实现》部分暂未完善,以后有时间再来补充。见谅!
文中为方便理解,会将接口在用到的时候才导入,实际中应在文件开始统一导入。
三、**算法实现
四、接口实现
1、API
sklearn.svm.SVC
导入:
from sklearn.svm import SVC
语法:
SVC(C=1.0, kernel=‘rbf’, degree=3, gamma=‘auto’,
coef0=0.0, shrinking=True, probability=False,tol=0.001,
cache_size=200, class_weight=None, verbose=False, max_iter=-1,
decision_function_shape=None,random_state=None)
C:惩罚参数,默认值是1.0。
C越大,表示越不允许分类出错,这样对训练集测试时准确率很高,但泛化能力弱。
C值小,对误分类的惩罚减小,允许容错,将他们当成噪声点,泛化能力较强。
Kernel:核函数,默认是rbf,
‘linear’:为线性核,C越大分类效果越好,但可能会过拟合;
‘rbf’:为高斯核,gamma值越小,分类界面越连续;gamma值越大,分类界面越“散”,分类效果越好,但可能会过拟合;
‘poly’:多项式核
‘sigmoid’:Sigmoid核函数
‘precomputed’:核矩阵
decision_function_shape :‘ovo’, ‘ovr’ or None, default=None
'ovr'时,为one v rest,即一个类别与其他ov类别进行划分;
'ovo'时,为one v one,即将类别两两进行划分,用二分类的方法模拟多分类的结果;
degree :多项式poly函数的维度,默认是3,选择其他核函数时会被忽略。
gamma :‘rbf’,‘poly’ 和‘sigmoid’的核函数参数。默认是’auto’,则会选择1/n_features
coef0 :核函数的常数项。对于‘poly’和 ‘sigmoid’有用。
probability :是否采用概率估计?.默认为False
shrinking :是否采用shrinking heuristic方法,默认为true
tol :停止训练的误差值大小,默认为1e-3
cache_size :核函数cache缓存大小,默认为200
class_weight :类别的权重,字典形式传递。设置第几类的参数C为weightC(C-SVC中的C)
verbose :允许冗余输出
max_iter :最大迭代次数。-1为无限制。
random_state :数据洗牌时的种子值,int值
SVC.coef_:权重
SVC.intercept_:偏置sklearn.svm.LinearSVC
导入:
from sklearn.svm import LinearSVC
语法:
sklearn.svm.LinearSVC(penalty='l2', loss='squared_hinge', dual=True, C=1.0)
参数:
penalty:正则化参数,L1和L2两种参数可选,仅LinearSVC有。
loss:损失函数,
有hinge和squared_hinge两种可选,前者⼜称L1损失,后者称为L2损失,默认是squared_hinge,
其中hinge是SVM的标准损失,squared_hinge是hinge的平方
dual:是否转化为对偶问题求解,默认是True。
C:惩罚系数,
属性:
LinearSVC.coef_:权重
LinearSVC.intercept_:偏置
方法:
fix(x,y): 训练模型
predict(x): 用模型进行预测,返回预测值
score(x,y[, sample_weight]):返回在(X, y)上预测的准确率2、线性可分SVM(硬间隔)流程
2.1、获取数据
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
# 获取数据
iris = load_iris()2.2、数据预处理
x=iris.data[:,(2,3)]
y=iris.target
setosa_or_versicolor=(y==0)|(y==1)
x=x[setosa_or_versicolor]
y=y[setosa_or_versicolor]
# 划分数据集
x_train,x_test,y_train,y_test = train_test_split(x, y, test_size=0.2, random_state=1473) 2.3、特征工程
2.4、模型训练
# 实例化学习器
model_svc = SVC(kernel='linear',C=float("inf"))
# 模型训练
model_svc.fit(x_train,y_train)
print("建立的支持向量机模型为:\n", model_svc)2.5、模型评估
# 用模型计算测试值,得到预测值
y_pred=model_svc.predict(x_test)
print('前20条记录的预测值为:\n', y_pred[:20])
print('前20条记录的实际值为:\n', y_test[:20])
# 求出预测准确率和混淆矩阵
from sklearn.metrics import accuracy_score, confusion_matrix
print("预测结果准确率为:", accuracy_score(y_test, y_pred))
print("预测结果混淆矩阵为:\n", confusion_matrix(y_test, y_pred))2.6、结果预测
经过模型评估后通过的模型可以代入真实值进行预测。
2.7、可视化
x=iris.data[:,(2,3)]
y=iris.target
w=model_svc.coef_[0]
b=model_svc.intercept_[0]
x0=np.linspace(0,5.5,200)
decision_boundary=-w[0]/w[1]*x0-b/w[1]
margin=1/w[1]
gutter_up=decision_boundary+margin
gutter_down=decision_boundary-margin
# 可视化
plt.figure(figsize=(14,8))
# 数据点
plt.plot(x[:,0][y==1],x[:,1][y==1],'bs')
plt.plot(x[:,0][y==0],x[:,1][y==0],'ys')
# 支持向量
svs=model_svc.support_vectors_
plt.scatter(svs[:,0],svs[:,1],s=180,facecolors='red')
# 决策边界和决策超平面
plt.plot(x0,decision_boundary,'k-',linewidth=2)
plt.plot(x0,gutter_up,'k--',linewidth=2)
plt.plot(x0,gutter_down,'k--',linewidth=2)
#
plt.axis([0,5.5,0,2]) 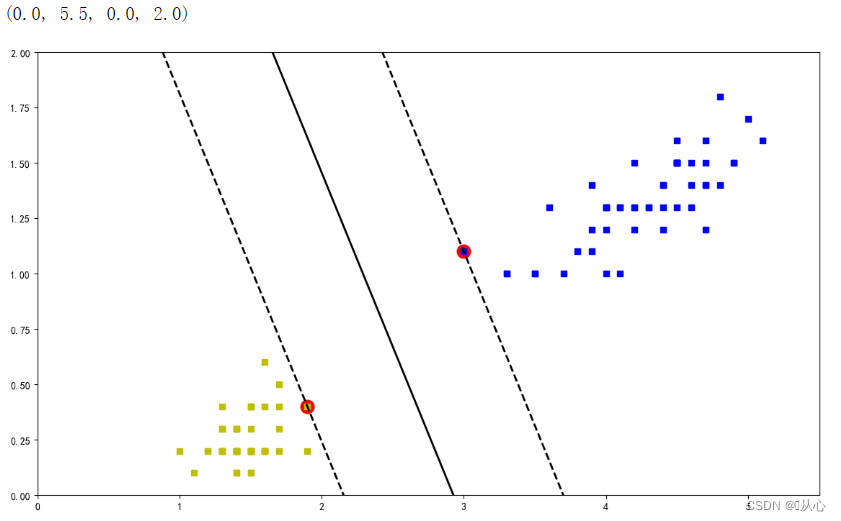
3、线性SVM(软间隔)流程
3.1、获取数据
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
# 获取数据
iris = load_iris()3.2、数据预处理
x=iris.data[:,(2,3)]
y=(iris.target==2).astype(np.float64)3.3、特征工程
3.4、模型训练
实现线性SVM用LinearSVC试试
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
svm_clf=Pipeline((
('std',StandardScaler()),
('linear_svc',LinearSVC(C = 1))
))
svm_clf.fit(x,y)
3.5、模型评估
3.6、结果预测
经过模型评估后通过的模型可以代入真实值进行预测。
svm_clf.predict([[5.5,1.7]]) 
3.7、可视化(不同C值带来的效果差异)
scaler = StandardScaler()
svm_clf1=SVC(kernel='linear',C=1,random_state=1473)
svm_clf2=SVC(kernel='linear',C=100,random_state=1473)
# scaled_svm_clf1=Pipeline((
# ('std',StandardScaler()),
# ('linear_svc',svm_clf1)
# ))
# scaled_svm_clf2=Pipeline((
# ('std',StandardScaler()),
# ('linear_svc',svm_clf2)
# ))
# scaled_svm_clf1.fit(x,y)
# scaled_svm_clf2.fit(x,y)
svm_clf1.fit(x,y)
svm_clf2.fit(x,y)# 绘制决策边界
def plot_svc_decision_boundary(clf,sv=True):
w=clf.coef_[0]
b=clf.intercept_[0]
x0=np.linspace(0,5.5,200)
decision_boundary=-w[0]/w[1]*x0-b/w[1]
margin=1/w[1]
gutter_up=decision_boundary+margin
gutter_down=decision_boundary-margin
if sv:
svs=clf.support_vectors_
plt.scatter(svs[:,0],svs[:,1],s=180,facecolors='red')
plt.plot(x0,decision_boundary,'k-',linewidth=2)
plt.plot(x0,gutter_up,'k--',linewidth=2)
plt.plot(x0,gutter_down,'k--',linewidth=2)plt.figure(figsize=(14,4))
plt.subplot(121)
# 数据点
plt.plot(x[:,0][y==1],x[:,1][y==1],'bs',label="Iris-Virginica")
plt.plot(x[:,0][y==0],x[:,1][y==0],'ys',label="Iris-Versicolor")
# 决策边界和决策超平面
plot_svc_decision_boundary(svm_clf1,sv=True)
plt.xlabel("Petal length",fontsize=14)
plt.ylabel("Petal width",fontsize=14)
plt.legend(loc="upper left",fontsize=14)
plt.title("$C={}$".format(svm_clf1.C),fontsize=16)
plt.axis([4,6,0.5,3])
plt.subplot(122)
# 数据点
plt.plot(x[:,0][y==1],x[:,1][y==1],'bs',label="Iris-Virginica")
plt.plot(x[:,0][y==0],x[:,1][y==0],'ys',label="Iris-Versicolor")
# 决策边界和决策超平面
plot_svc_decision_boundary(svm_clf2,sv=True)
plt.xlabel("Petal length",fontsize=14)
plt.ylabel("Petal width",fontsize=14)
plt.legend(loc="upper left",fontsize=14)
plt.title("$C={}$".format(svm_clf2.C),fontsize=16)
plt.axis([4,6,0.5,3])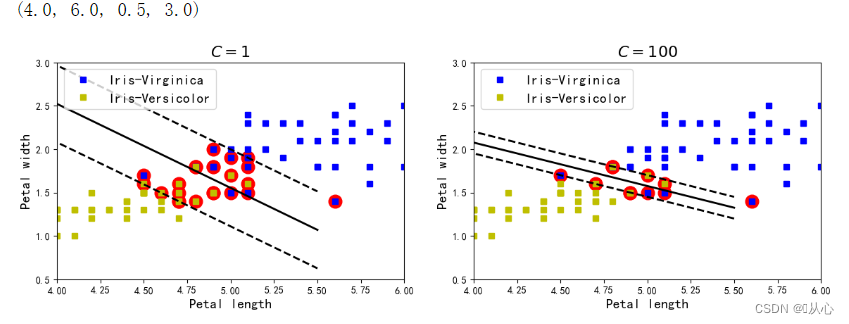
4、非线性可分SVM(核技巧)
4.1、升维转换演示
x1D=np.linspace(-4,4,9).reshape(-1,1)
x2D=np.c_[x1D,x1D**2]
y=np.array([0,0,1,1,1,1,1,0,0])
plt.figure(figsize=(11,4))
plt.subplot(121)
plt.grid(True,which='both')
plt.axhline(y=0,color='k')
plt.plot(x1D[:,0][y==0],np.zeros(4),'bs')
plt.plot(x1D[:,0][y==1],np.zeros(5),'g^')
plt.gca().get_yaxis().set_ticks([])
plt.xlabel(r"$x_1$",fontsize=20)
plt.axis([-4.5,4.5,-0.2,0.2])
np.zeros(4)
x1D=np.linspace(-4,4,9).reshape(-1,1)
x2D=np.c_[x1D,x1D**2]
y=np.array([0,0,1,1,1,1,1,0,0])
plt.figure(figsize=(11,4))
plt.subplot(121)
plt.grid(True,which='both')
plt.axhline(y=0,color='k')
plt.plot(x1D[:,0][y==0],np.zeros(4),'bs')
plt.plot(x1D[:,0][y==1],np.zeros(5),'g^')
plt.gca().get_yaxis().set_ticks([])
plt.xlabel(r"$x_1$",fontsize=20)
plt.axis([-4.5,4.5,-0.2,0.2])
np.zeros(4)
plt.subplot(122)
plt.grid(True,which='both')
plt.axhline(y=0,color='k')
plt.axvline(x=0,color='k')
plt.plot(x2D[:,0][y==0],x2D[:,1][y==0],'bs')
plt.plot(x2D[:,0][y==1],x2D[:,1][y==1],'g^')
plt.xlabel(r"$x_1$",fontsize=20)
plt.xlabel(r"$x_2$",fontsize=20,rotation=0)
plt.gca().get_yaxis().set_ticks([0,4,8,12,16])
plt.plot([-4.5,4.5],[6.5,6.5],'r--',linewidth=3)
plt.axis([-4.5,4.5,-1,17])
plt.subplots_adjust(right=1)
plt.show() 4.2、线性核
4.2、线性核
4.2.1、创建非线性数据
from sklearn.datasets import make_moons
x,y=make_moons(n_samples=100,noise=0.15,random_state=1473)
# 创建非线性数据
def plot_dataset(x,y,axes):
plt.plot(x[:,0][y==0],x[:,1][y==0],'bs')
plt.plot(x[:,0][y==1],x[:,1][y==1],'g^')
plt.axis(axes)
plt.grid(True,which='both')
plt.xlabel(r"$x_1$",fontsize=20)
plt.xlabel(r"$x_2$",fontsize=20,rotation=0)
plot_dataset(x,y,[-1.5,2.5,-1,1.5])
plt.show() 
4.2.2、分类预测
使用PolynomialFeatures模块进行预处理,使用这个可以增加数据维度
polynomial_svm_clf.fit(X,y)对当前进行训练传进去X和y数据
# 分类预测
from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
polynomial_svm_clf=Pipeline((("poly_features",PolynomialFeatures(degree=3)),
("scaler" ,StandardScaler()),
("svm_clf",LinearSVC(C=10,loss="hinge"))))
polynomial_svm_clf.fit(x,y)
def plot_predictions(clf,axes):
x0s=np.linspace(axes[0],axes[1],100)
x1s=np.linspace(axes[2],axes[3],100)
x0,x1=np.meshgrid(x0s,x1s)
x=np.c_[x0.ravel(),x1.ravel()]
y_pred=clf.predict(x).reshape(x0.shape)
plt.contourf(x0,x1,y_pred,cmap=plt.cm.brg,alpha=0.2)
plot_predictions(polynomial_svm_clf,[-1.5,2.5,-1,1.5])
plot_dataset(x,y,[-1.5,2.5,-1,1.5])
4.3、多项式核函数
poly_kernel_svm_clf=Pipeline([
("scaler",StandardScaler()),
("svm_clf",SVC(kernel='poly',degree=3,coef0=1,C=5))
])
poly_kernel_svm_clf.fit(x,y) 
poly100_kernel_svm_clf=Pipeline([
("scaler",StandardScaler()),
("svm_clf",SVC(kernel='poly',degree=10,coef0=100,C=5))
])
poly100_kernel_svm_clf.fit(x,y)
plt.figure(figsize=(11,4))
plt.subplot(121)
plot_predictions(poly_kernel_svm_clf,[-1.5,2.5,-1,1.5])
plot_dataset(x,y,[-1.5,2.5,-1,1.5])
plt.title(r"$d=3,r=1,C=5$")
plt.subplot(122)
plot_predictions(poly100_kernel_svm_clf,[-1.5,2.5,-1,1.5])
plot_dataset(x,y,[-1.5,2.5,-1,1.5])
plt.title(r"$d=10,r=100,C=5$")
plt.show() 
4.4、高斯(径向基)RBF核函数
import numpy as np
from matplotlib import pyplot as plt
## 构造数据
X1D = np.linspace(-4, 4, 9).reshape(-1, 1)
X2D = np.c_[X1D, X1D ** 2]
y = np.array([0, 0, 1, 1, 1, 1, 1, 0, 0])
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.15, random_state=42) #指定两个环形测试数据
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline ##使用操作流水线
from sklearn.preprocessing import StandardScaler
## 通过设置degree值来进行对比实验
poly_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5)) ##coef0表示偏置项
])
poly_kernel_svm_clf.fit(X, y)
poly100_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=100, coef0=1, C=5))
])
poly100_kernel_svm_clf.fit(X, y)
# 制图展示对比结果
def plot_predictions(clf, axes):
xOs = np.linspace(axes[0], axes[1], 100)
x1s = np.linspace(axes[2], axes[3], 100)
x0, x1 = np.meshgrid(xOs, x1s) ##构建坐标棋盘
X = np.c_[x0.ravel(), x1.ravel()]
y_pred = clf.predict(X).reshape(x0.shape) #一定要对预测结果进行reshape操作
plt.contourf(x0, x1, y_pred, cmap=plt.cm.brg, alpha=0.2)
def plot_dataset(X, y, axes):
plt.plot(X[:, 0][y == 0], X[:, 1][y == 0], "bs")
plt.plot(X[:, 0][y == 1], X[:, 1][y == 1], "g^")
plt.axis(axes)
plt.grid(True, which='both')
plt.xlabel(r"$x_1$", fontsize=20)
plt.ylabel(r"$x_2$", fontsize=20, rotation=0)
plt.figure(figsize=(11, 4))
plt.subplot(121)
plot_predictions(poly_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.title(r"$d=3,r=1,C=5$", fontsize=18)
plt.subplot(122)
plot_predictions(poly100_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.title(r"$d=10,r=100,C=5$", fontsize=18)
plt.show()
# 定义高斯核函数
def gaussian_rbf(x, landmark, gamma):
'''
:param x: 待变换数据
:param landmark:当前选择位置
:param gamma:(不同γ值对公式会产生不同的影响)
:return:
'''
return np.exp(-gamma * np.linalg.norm(x - landmark, axis=1) ** 2)gamma = 0.3
x1s = np.linspace(-4.5, 4.5, 200).reshape(-1, 1)
##分别选择不同的地标将数据进行映射
x2s = gaussian_rbf(x1s, -2, gamma)
x3s = gaussian_rbf(x1s, 1, gamma)
XK = np.c_[gaussian_rbf(X1D, -2, gamma), gaussian_rbf(X1D, 1, gamma)]
yk = np.array([0, 0, 1, 1, 1, 1, 1, 0, 0])
plt.figure(figsize=(11, 4))
###绘制变换前数据分布已经变换过程
plt.subplot(121)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.scatter(x=[-2, 1], y=[0, 0], s=150, alpha=0.5, c="red")
plt.plot(X1D[:, 0][yk == 0], np.zeros(4), "bs")
plt.plot(X1D[:, 0][yk == 1],np.zeros(5), "g^")
plt.plot(x1s, x2s, "g-")
plt.plot(x1s, x3s, "b:")
plt.gca().get_yaxis().set_ticks([0, 0.25, 0.5, 0.75, 1])
plt.xlabel(r"$x_1$", fontsize=20)
plt.ylabel(r"Similarity", fontsize=14)
plt.annotate(r'$\mathbf{x}$',
xy=(X1D[3, 0], 0),
xytext=(-0.5, 0.20),
ha="center",
arrowprops=dict(facecolor='black', shrink=0.1),
fontsize=18, )
plt.text(-2, 0.9, "Sx_2s", ha="center", fontsize=20)
plt.text(1, 0.9, "Sx_3S", ha="center", fontsize=20)
plt.axis([-4.5, 4.5, -0.1, 1.1])
###绘制最终结果与分界线
plt.subplot(122)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')
plt.plot(XK[:, 0][yk == 0], XK[:, 1][yk == 0], "bs")
plt.plot(XK[:, 0][yk == 1], XK[:, 1][yk == 1], "g^")
plt.xlabel(r"$x_2$", fontsize=20)
plt.ylabel(r"$x_3$", fontsize=20, rotation=0)
plt.annotate(r'$\phi\left (\mathbf{x}\right)$',
xy=(XK[3, 0], XK[3, 1]),
xytext=(0.65, 0.50),
ha="center",
arrowprops=dict(facecolor='black', shrink=0.1),
fontsize=18, )
plt.plot([-0.1, 1.1], [0.57, -0.1], "r--", linewidth=3)
plt.axis([-0.1, 1.1, -0.1, 1.1])
plt.subplots_adjust(right=1)
plt.show()
### 探讨γ值与C值对模型结果的影响'''
from sklearn.svm import SVC
gamma1, gamma2 = 0.1, 5
C1, C2 = 0.001, 1000
hyperparams = (gamma1, C1), (gamma1, C2), (gamma2, C1), (gamma2, C2)
svm_clfs = []
for gamma, C in hyperparams:
rbf_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="rbf", gamma=gamma, C=C))
])
rbf_kernel_svm_clf.fit(X, y)
svm_clfs.append(rbf_kernel_svm_clf)
plt.figure(figsize=(11, 7))
for i, svm_clf in enumerate(svm_clfs):
plt.subplot(221 + i)
plot_predictions(svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
gamma, C = hyperparams[i]
plt.title(r'$\gamma={},C={}$'.format(gamma, C), fontsize=16)
plt.show() 
旧梦可以重温,且看:机器学习(五) -- 监督学习(7) --SVM1
欲知后事如何,且看: